Задача 1

Имеется длинный прямой проводник с током, на расстояния а и b от него расположены два параллельных ему провода, замкнутых на одном конце сопротивлением R. По проводу без трения перемещают с V=const стержень-перемычку. Пренебрегая сопротивлением проводов стержня, найти: 1) индукционный ток I_i в стержне; 2) F – силу, необходимую для поддержания V=const стержня.

а)

1) (1) - неоднородное поле.

2) В момент времени t выберем элементарную площадку dS = dr∙x; x = V^.t, т.к. V=const.

dS = Vt^.dr;

(2)

3) (3)

4) (4)

б) На стержень с током действует со стороны магнитного поля В сила Ампера F_A = - F, где F – внешняя сила, приложенная к стержню.

Т.к. В ≠ const, то для расчета F_A применяем ДИМ.

dl = dr – элемент стержня → dF_A = I_idl^.BSin90⁰ →dF_A = I_idrB →

(5).

В эту формулу поставляем (4):

На рисунке даны графики изменения магнитного потока, пронизывающие один и тот же проводящий контур. Сравните заряды, протекшие по контуру за время τ.

Варианты ответа: 1) q₁ > q₂; 2) 2) q₁ < q₂;

3) q₁ = q₂; 4) q₁ = q₂ = 0.

Контур с током

1. Магнитный момент плоского контура с током

,

2. Сила, действующая на контур с током

Если В = const (однородное поле), то сила Ампера, действующая на контур с током равна нулю.

Если В ≠ const, то

3. Момент сил, действующих на контур с током

В = const : М = [p_m ,B] M = p_mBSinα

Если p_m В, то α = 0 и М = 0 – это положение контура будет устойчивым.

Если p_m В, то α = π и М = 0, то такое положение контура является неустойчивым: малейшее отклонение от этого положения приведет к моменту сил, стремящегося отклонить контур еще больше от начального положения.

1. Рамка стоком с магнитным дипольным моментом, направление которого указано на рис. находится в однородном магнитном поле. Момент сил, действующих на диполь, направлен…

1) перпендикулярно плоскости рис. от нас;

2) перпендикулярно плоскости рис. к нам;

3) по направлению вектора В;

4) противоположно направлению вектора В.

Магнитное поле в веществе

Все вещества, помещенные в магнитное поле намагничиваются, т.е. являются магнетиками. Гипотеза Ампера:

В любом веществе существуют микротоки, обусловленные движением электронов в атомах и молекулах. Их еще называют молекулярными токами.

Приближенно можно считать, что электрон в атоме движется по круговой орбите. Тогда движущийся электрон эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом: p_m =ISn , где I – сила тока.

Магнетики по своим магнитным свойствам подразделяются на 3основные группы: 1) диамагнетики; 2) парамагнетики; 3) ферромагнетики.

- результирующее поле.

В₀ – внешнее магнитное поле (поле, создаваемое током в вакууме – поле токов проводимости);

B` - поле микротоков (поле токов намагничивания).

- намагниченность.

В несильных полях: J _˜ H , т.е. , где χ – магнитная восприимчивость вещества, χ - безразмерная величина. χ _Д < 0 – для диамагнетиков, т.к. поле микротоков противоположно внешнему.

χ _П > 0 – для парамагнетиков (поле микротоков совпадает с внешним).

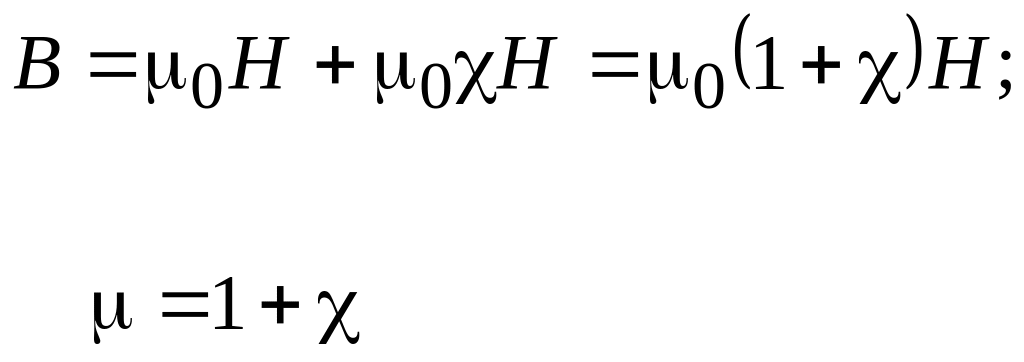μ - магнитная проницаемость вещества .

Т.к., χ для диа- и парамагнетиков очень мало (порядка 10^-6-10^-4), то μ ≈ 1.

χ _Д < 0 и μ_Д ≤ 1 – для диамагнетиков

χ _П > 0 и μ_П ≥ 1 – для парамагнетиков.

χ _Д ≠ f (T)

χ _П = f (T) по закону Кюри: ,

С – const Кюри, C зависит от рода вещества: , n – концентрация атомов; р_ma - магнитный момент атома.