Соединение конденсаторов

Е сли соединяются обкладки с зарядами одного знака, речь идет о параллельном соединении конденсаторов, если с разноименными зарядами – о последовательном.

Действия с конденсатором

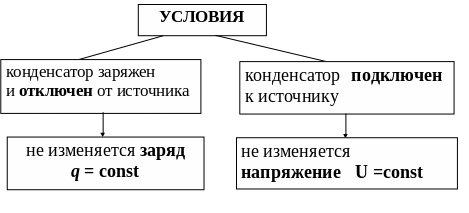
9. Емкость плоского конденсатора С₁ = 10^-10 Ф. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов U₁ = 600 В и отключили от источника. Какую работу необходимо совершить, чтобы вынуть диэлектрик из конденсатора? Трением пренебречь.

Если конденсатор отключили от источника, то напряжение уменьшается, но остается q = const. Энергия конденсатора: Т.к. q=const, то необходимо использовать формулу . А_внеш. = W₂ – W₁

.

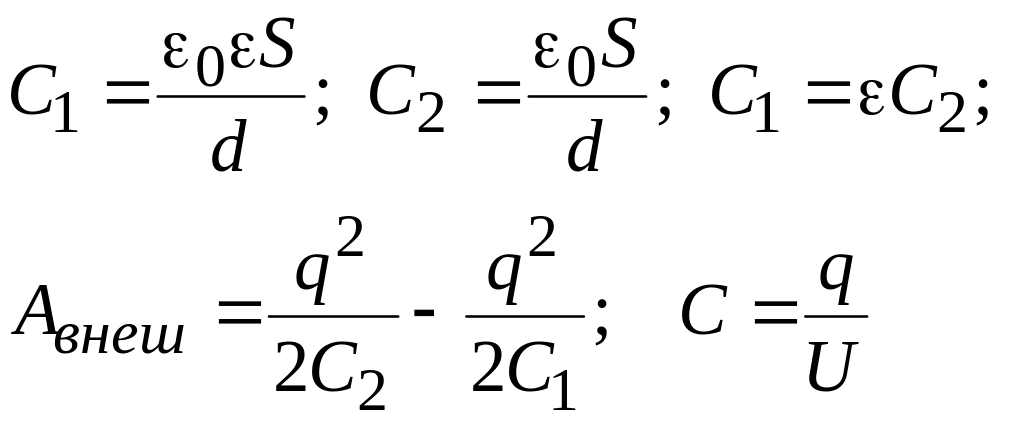
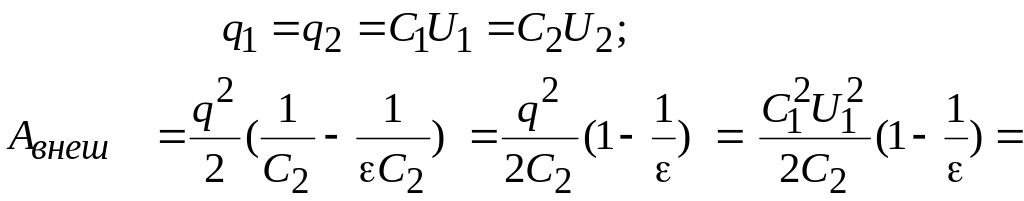
Если конденсатор остается подключенным к источнику, то q ≠ const, а

U = const = q₁/C₁ = q₂/C₂ и W = ½ (CU²).

10. Плоский конденсатор электроемкостью 4нФ подсоединен к источнику напряжения 10 В. Затем, не отключая конденсатор от источника, расстояние между его обкладками увеличили в 2 раза.

1) Найти, во сколько раз изменились следующие величины: а) электроемкость конденсатора, б) заряд на его обкладках, в) напряжение на конденсаторе, г) поверхностная плотность заряда, д) напряженность электростатического поля, е) поток Е через пластину конденсатора,

ж) электрическая индукция D, з) плотность энергии электрического поля в конденсаторе,

и) энергия конденсатора.

2) Рассчитать работу, затраченную на изменение расстояния между обкладками.

3) Найти заряд, прошедший через источник.

1) а) если С₁ = 4 нФ, то

С₂ = 2 нФ и С₂ / С₁ = ½.

в) Т.к. конденсатор от источника не отключается, то U₂ = U₁ = U =10 B, но изменяется заряд:

б) q₁ = C₁U, q₂ = C₂U → q₂ / q₁ = ½.

г) → σ₂ / σ₁ = ½. д) Е₂ / Е₁ = ½.

е) N_E = ES , N_E2 / N_E1 = ½. ж) → D₂ /D₁ = ½.

з) w = ½ ε₀εE ² → w₂ / w₁ = ¼.

и) Когда U = const, то W = ½CU ²,

то W₂ / W₁ = ½.

2) Работа внешних сил, затраченная на изменение расстояние между обкладками, рассчитывается как изменение энергии конденсатора:

A= W₂ - W₁ = ½ W₁ - W₁ = - ½ W₁ = - ¼ C₁U² = - 10^-7 Дж.

3) Найдем заряд, прошедший через источник:

∆q = q₁ - q₂ = q₁ - ½ q₁ = ½ q₁= ½ C₁U = 2∙10^-8 Кл.

Энергия электростатического поля

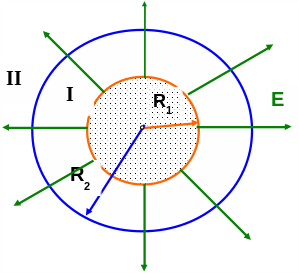
14. Уединенный металлический шар R₁ = 6 см несет некоторый заряд. Концентрическая этой сфере поверхность делит пространство на две части (внутренняя – конечная и внешняя – бесконечная) так, что энергия электрического поля обеих частей одинаковы. Определить радиус этой сферы R_2.

Р е ш е н и е

Применяем ДИМ, т.к. поле неоднородное.

По условию W_I = W_II

E₁ = 0 – внутри

проводника

- на поверхности шара.

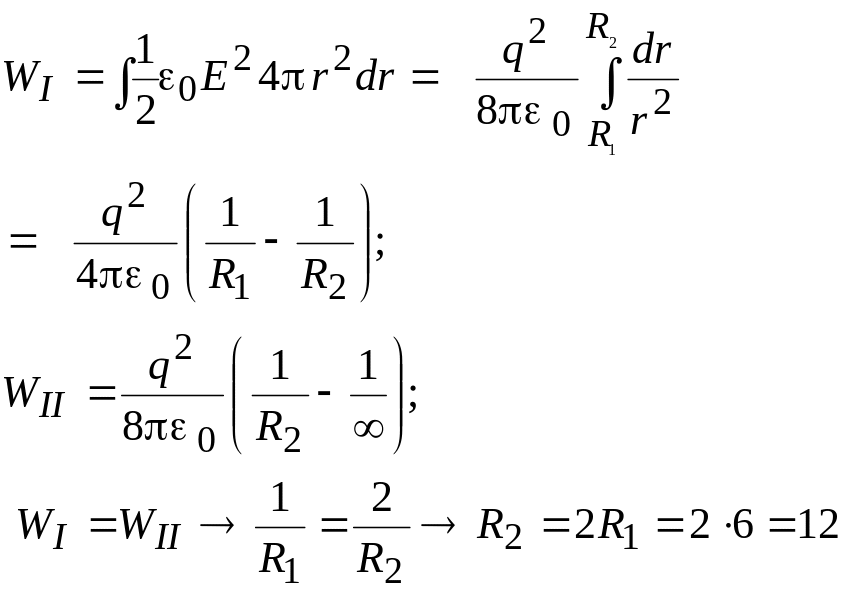
ЭЛЕКТРОМАГНЕТИЗМ

1. Закон Био-Савара-Лапласа

I = const

2. Поле точечного заряда, движущегося с V=const и V« С

1 ) Поле прямолинейного тока

Для бесконечного проводника: α₁ = 0 и α₂ = π

Поле кругового тока

1. На рисунке изображено сечение проводника с током I. Укажите направление вектора магнитной индукции в т.А .

2. I₁ = 2I₂ В какой точке интервала Врез = 0?

1) d; 1) a; 2) b; 3) c; 4) d

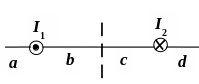
- поле длинного проводника с током.

3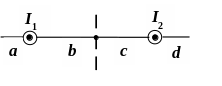 . I₁ < I₂ В какой точке интервала Врез = 0?

4 . Два прямолинейных бесконечно длинных проводника с равными по величине токами расположены взаимно перпендикулярно в одной плоскости. В каких квадрантах находятся точки, в которых индукция магнитного поля обращается в нуль ?

3 . На рисунке изображены сечения трех проводников, расположенных в вершинах квадрата (проводники линейные, бесконечно длинные, прямые). Определить направление вектора магнитной индукции в четвертой вершине квадрата.

3 . На рис. изображен вектор скорости движения электрона. Вектор В поля, создаваемого электроном при движении в точке С направлен… 1) от нас; 2) сверху вниз; 3) снизу верх; 4) на нас.

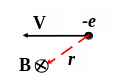→ Вектор В поля направлен по правилу левой руки, если q>0; по правилу правой руки, если q<0, т.е. от нас.