Электростатика (практика) теорема гаусса

;

Поток вектора Е сквозь произвольную поверхность S:

Алгоритм применения теоремы

1) Сформулировать и записать математическое выражение теоремы.

2) Сделать рисунок распределения заряда и определить тип симметрии.

3) Изобразить на рисунке силовые линии электрического поля.

4) Выбрать и нарисовать гауссову поверхность.

5) Записать выражение для потока N через построенную поверхность.

6) Найти заряд q, находящийся внутри объема, ограниченного гауссовой поверхностью.

7) Подставить выражения для N и q в формулу теоремы, найти Е.

Требования к построению гауссовой поверхности

1. Форма S должна соответствовать типу симметрии распределения заряда.

2. Поверхность S должна проходить через точку, в которой требуется определить поле.

3. На S или ее части напряженность Е поля должна быть направлена по нормали и принимать одинаковые значения Е = Е_n = const или нормальная составляющая

E_n = 0.

1. Можно ли применить для вычисления потока вектора Е формулу N = ES в случаях:

1) поверхность цилиндрическая, вдоль ее оси направлена бесконечная равномерно заряженная нить;

2) поверхность цилиндрическая, на ее оси находится заряженная равномерная нить АВ, длина которой соизмерима с высотой цилиндра;

3) поверхность - основание указанного выше цилиндра.

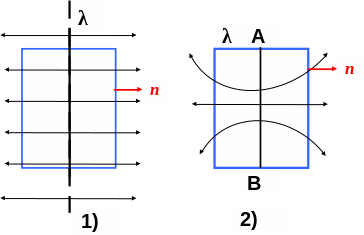
1) В этом случае поле обладает радиальной симметрией. Поэтому на боковой цилиндрической поверхности цилиндра Е = Е_n = const, формулу N = ES можно применять.

Для основания цилиндра в этом случае

Е_n = 0, т.е. данную формулу применить

нельзя (3).

2) В случае конечной длины нити на боковой цилиндрической поверхности цилиндра → .

Для основания цилиндра в этом случае , т.е. данную формулу применить нельзя (3).

2. Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q за пределами сферы то поток вектора Е через поверхность сферы…

Варианты ответа: 1) не изменится ; 2) увеличится; 3)уменьшится.

3. Дана система точечных зарядов в вакууме и замкнутые поверхности S₁, S₂ и S₃. Поток вектора Е электростатического поля отличен от нуля через поверхности…

Варианты ответа: 1) S₁; 2) S₂; 3) S₃.

4. Симметричное сферическое облако ионизированных частиц расширяется. Изменяются ли: 1) поток вектора напряженности N через поверхность облака, 2) напряженность поля на границе облака ?

5. Найти напряженность поля, созданного бесконечным слоем с внутренним радиусом R₁ и внешним - R₂ , заряженным с постоянной объемной плотностью ρ.

;

ρ = q/V

1. r₁ < R₁

q = 0 → E₁ = 0

2. R₁ < r₂ < R₂

3. r₃ > R₂

6.

C ферический конденсатор представляет собой две концентрические сферы радиусов R₁ и R₂ (R₁< R₂). Заряды на внутренней и внешней сферах равны соответственно +q и – q. Определить Е и φ внутри сферы радиуса R₁, между сферами и вне сфер.

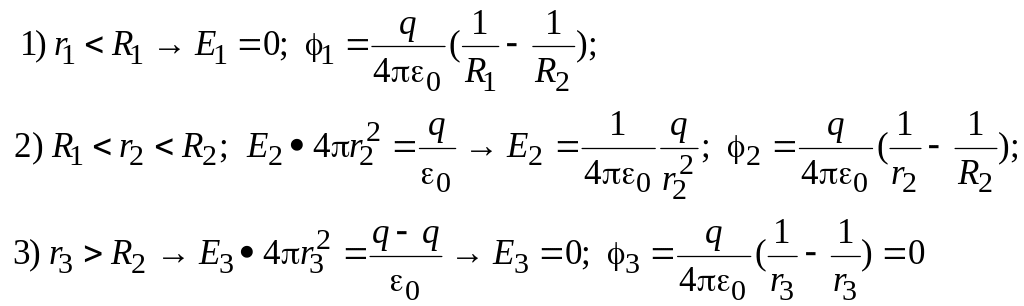
7 .Заряд распределен симметрично относительно плоскости S таким образом, что его объемная плотность зависит от координаты х, отсчитываемой от плоскости симметрии, по закону:

₁ = ₀ при |x| < a;

при |x| > a.

1. Используя теорему Гаусса, найти зависимость E(x) напряженности электростатического поля от координаты x для областей I, II. Принять ₀ = 0,1 мкКл/м³, a = 2 м;

2. построить график E(x).

ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

В ВЕЩЕСТВЕ

I.Поле в диэлектрике

Е = Е₀ + Е` → E = E<sub>0</sub> – E` → E = f(1/ε)

D = ε₀εE → D ≠ f(ε) D = ε₀E + P

Теорема Остроградского-Гаусса:

Граничные условия

E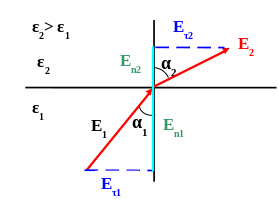 _1τ = E_2τ D_1n = D_2n

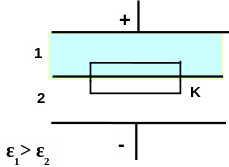
1. В двухслойном плоском конденсаторе (ε₁>ε₂) мысленно выделена поверхность в виде коробки К. Каков связанный заряд внутри нее?

В арианты ответа: 1) q`>0, 2) q`<0, 3) q`=0.

Решение

2. Плоский конденсатор наполовину расстояния между пластинами заполнен диэлектриком. Ход потенциала показан на Рис. Какая часть (1 или 2) заполнена диэлектриком?

Решение

E = f(1/ε) D = ε₀εE → D ≠ f(ε) → D₁ = D₂ = const

α₂ > α₁ → ε₁ – диэлектрик,

ε₂ – вакуум

3. Диэлектрическая пластина шириной 2а с ε=2 помещена в однородное электрическое поле Е, линии которого перпендикулярны пластине.

а) Изобразить на рисунке линии Е и D

б) Построить качественно графики зависимостей Е_х и D_x

в) Построить качественно график зависимости потенциала φ от х.

Ось х перпендикулярна пластине, вектор Е направлен вдоль х, точка х=0 находится на середине ширины пластины).

в)

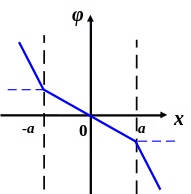
4. Указать верную подпись:

1) линии D, ε₁>ε₂

2) линии D, ε₁<ε₂

3 ) линии Е, ε₁>ε₂

4) линии Е, ε₁<ε₂

5. В поле точечного заряда q>0 находится палочка из диэлектрика. Выделены 3 сферические области S₁, S₂, S₃, в центре которых находится заряд q.

1) Сравнить потоки вектора Е через эти поверхности.

2) Сравнить потоки вектор D через эти же поверхности.

3) Можно ли найти D(r), используя теорему Гаусса?

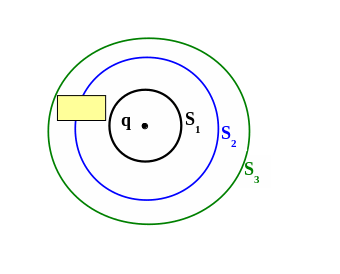
1) N_E1 = N_E3 > N_E2

2) N_D1 = N_D2 = N_D3

3) Палочка нарушает сферическую

симметрию, поэтому D(r) с помощью

теоремы Гаусса определить нельзя.

6 . Рассмотрим т.А вблизи заряда +q. Изменятся ли Е и φ в т.А, если заряд q и т.А окружить сферическим слоем диэлектрика с центром в точке, где находится заряд q ? Варианты ответа: 1) Да; 2) Нет.

Р

d

е ш е н и е

1 ) Через т.А проведем гауссову поверхность в виде сферы с центром, где находится +q. Поэтому Е поля в т.А не меняется.

2) Потенциал φ поля в т.А уменьшается. Это можно показать различными способами:

а) Используем принцип суперпозиции.

В результате поляризации возникают связанные заряды: -q′ и +q′. Т.о., φ_А = φ_q – φ′_- + φ′₊

φ = f(1/r), поэтому /φ′_-/ ≥ /φ`₊/. Т.о., φ_А уменьшается.

б) - определение потенциала. q′φ_1∞=A_1∞ = F S = q′ES.

, где F₀ – сила в вакууме, F – сила в среде ε. Т.о., работа, а значит, и потенциал в т.А

уменьшается.

в ) Эту задачу можно решить, используя связь между Е и φ:

Кривая 1 (красного цвета) соответствует полю точечного заряда в вакууме . E = f(1/ε) - в среде.

Кривая 2 (синего цвета) – поле точечного заряда, окруженного слоем диэлектрика (внутри слоя Е уменьшается в ε раз). φ_А определяется площадью под кривой E(r), исходя из геометрического смысла интеграла : Сравнивая площади под кривыми 1 и 2, приходим к выводу, что φ_А уменьшается.

7. В центре сферической поверхности находится точечный заряд q. Изменится ли поток вектора D через поверхность, если а) все пространство заполнить диэлектриком; б) заменить сферическую поверхность кубической?

8. Вокруг точечного заряда q в диэлектрике с полярными молекулами проведена сфера. Как изменятся N_E и N_D через сферу, если а) диэлектрик нагреть; б) увеличить плотность вещества?

; D ≠ f(ε); - для полярного диэлектрика; ε = 1 +χ.

а) Е уменьшается в диэлектрике, поэтому из теоремы Гаусса следует: N_E увеличивается, а N_D не изменяется.

б) n – концентрация. Если увеличить n, то и ε увеличится и N_E уменьшается, N_D не

изменяется.

9 . Точечный заряд q находится в центре диэлектрического шара. Отличны ли от нуля интегралы:

по замкнутой поверхности S, частично захватывающей диэлектрик?

10. Имеется однородный равномерно и положительно заряженный по объему шар. Как изменяется поток вектора Е через единицу площади сферы, концентрической с шаром, при увеличении ее радиуса, если она располагается: 1) внутри шара; 2) снаружи (ε = 1)?

11. Дан бесконечно длинный цилиндрический равномерно заряженный по объему диэлектрический стержень. Определить зависимость потока вектора Е сквозь мысленно построенную цилиндрическую поверхность от ее радиуса r , если эта поверхность соосна со стержнем и проходит внутри его. Диэлектрик однородный.

Варианты ответа: 1) N ~ r; 2) N ~ r²;

3) N ~ r ^-1; 4) N = const.

12.

Н а рисунке представлены графики отражающие характер зависимости поляризованности диэлектрика от напряженности Е. Укажите зависимость соответствующую различным типам диэлектриков.