2.2. Свойства криволинейного интеграла второго рода.

1) При смене ориентации кривой на противоположный криволинейный интеграл второго рода меняет знак, т.е. если кривая отличается от кривой Г только ориентацией, символически , то для любого векторного поля G:

2) Аддитивность. Пусть точка С на кривой (ориентированной кривой) Г делит его на две кривых и с той же ориентацией, т.е. , символически , то

(точнее, если существуют оба интеграла в правой части, то существует интеграл, стоящий слева и равен выражению, стоящему справа).

3) Линейность. Для любых чисел из и векторных полей Fи Gсправедливо равенство:

(точнее, если существуют оба интеграла в правой части, то существует интеграл, стоящий слева и равен выражению, стоящему справа).

4) Теорема об оценке. Если кривая Г имеет длину L, и в любой точке для векторного поля G(M)справедливо неравенство

то справедлива оценка

5) Связь с криволинейным интегралом первого рода. Пусть в любой точке векторное поле G(M) образует с касательным вектором к ориентированной кривой в этой точке угол ( вообще говоря, зависящим от точки М ), то

(слева стоит криволинейный интеграл второго рода, а справа - первого).

2.3. Вычисление криволинейного интеграла второго рода.

1) Основная формула для вычисления криволинейного интеграла второго рода, по сути, содержится во второй формой записи этого интеграла:

А именно, пусть в пространстве задана параметризация кривой

причем, заданная ориентация на Г соответствует изменению параметра tот и (возможно также, что ). Тогда и

(4)

2) В случае "двумерного" криволинейного интеграла второго рода данная формула вычисления выглядит уже не так громоздко:

3) Следующее формулы являются частными случаями предыдущих. Например, если на плоскости кривой Г задан явно: причем, ориентация кривой соответствует изменению от до (возможно, что a<b ) то в качестве параметра выступает , и предыдущая формула принимает такой вид:

4) Если же ориентированная кривая Г задана на плоскости в полярных координатах:

, где изменяется от до , то надо подставить формулы

И поэтому формула для вычислений криволинейного интеграла второго рода в полярных координатах принимает такой вид:

Замечание. Часто путем интегрирования (или его частью) в криволинейном интеграле являются отрезок кривой. Если начало и конец отрезка расположены соответственно в

точках и , то отрезок задаётся параметрическими уравнениями:

(5)

причем t изменяется от (точка ) до (точка ).

ПРИМЕР 1. Найти работу векторного поля вдоль одного витка винтовой кривой Г: направление от точки до точки (см. рис. 13).

Рис.13. К примеру 1.

Ориентация кривой Г соответствует убыванию параметра tот до . По формуле (4), искомая работа равна:

2.4. Связь криволинейных интегралов первого и второго рода.

Пусть на плоской кривой Г даны две произвольные точки и (см. рис. 14). Обозначим через 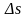длину кривой между точками и , через - абсциссу вектора , а через - его ординату. Из криволинейного треугольника (см. рис. 14) по теореме Пифагора получаем: Пусть - угол между вектором и осью абсцисс, а - угол между касательной к кривой Г в точке (предельным направлением вектора при ) и положительным направлением оси. Тогда при имеем . Кроме того, при малом значении можно считать, что . Поскольку 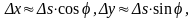то при получаем:

Рис.14. К выводу формулы связи криволинейных

интегралов первого и второго рода.

В случае пространственной кривой касательная в точке (предельное положение луча, направленного по вектору образует с координатными осями OX, OY, и OZ углы , соответственно, а вектор образует с теми же осями углы (см. рис. 15). При этом

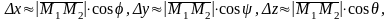
а Тогда в пределе при получаем:

Подставив эти соотношения в интегральные суммы для криволинейных интегралов первого и второго рода, приходим при (а значит, и ) к равенству соответствующих интегралов:

(1)

где - функции точки М.

Рис.15. К выводу формулы связи криволинейных

интегралов первого и второго рода.

Замечание. В двумерном случае (см. рис. 14) связь криволинейных интегралов первого и второго рода определяется формулой, аналогичной (1):

2.5. Физические приложения криволинейного интеграла второго рода. Начнём с вопроса о работе силы при перемещении материальной точки вдоль

некоторой траектории. В самом простом случае, когда точка перемещается вдоль прямой, а сила направлена в сторону движения точки, работа равна модулю силы, умноженному на величину перемещения . Если вектор составляет с направлением движения точки угол , но сама сила постоянна, то , т.е. работа равна произведению тангенциальной составляющей силы на величину перемещения. То же самое можно записать в виде скалярного произведения

(см. рис. 16).

Рис.16. Рис.17.

Теперь предположим, что движение происходит не по прямой, а по криволинейной траектории, а сила зависит от положения материальной точки . Чтобы сохранить предыдущие рассуждения, следует разбить траекторию на малые части,

причём каждую часть можно считать прямолинейной, а силу в пределах это части - постоянной, тогда на частичной дуге траектории работа силы равна 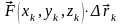(см. рис.17). Точка может быть выбрана любая в пределах данной частичной дуги (в силу малости дуги сила не зависит от выбора этой точки). Чтобы получить работу силы на всей траектории, нужно суммировать работы на всех частичных дугах:

Чтобы равенство стало точным, следует перейти к пределу разбиения траектории на бесконечно малые части. Предел является криволинейным интегралом второго рода: