1.6. Криволинейный интеграл первого рода от векторной функции.

_{Обычно криволинейный интеграл вычисляется от скалярной функции f(x,y,z), т.е. скалярного поля, и назначением этого интеграла является число, т.е. тоже скаляр. Но в принципе, криволинейный интеграл первого рода можно находить и от векторной функции, т.е. от векторного поля. А именно, если в пространстве заданы кривая Г и векторное поле}

то, по определению,

Понятно, что значение такого интеграла есть вектор.

1.7. Примеры на вычисление и приложения криволинейного интеграла первого рода.

ПРИМЕР 1. Найти площадь поверхности, полученной вращением кривой , вокруг прямой .

Перейдем к полярным координатам: получим: Тогда кривая Г - это половина одной петли лемнискаты Бернулли (см. рис.8). Расстояние от точки M(x,y)до прямой выражается формулой:

В данном случае

По формуле (2), площадь поверхности вращения равна

Рис.8. К примеру 1. Рис.9. Кпримеру2.

ПРИМЕР 2. Вычислить ньютонов потенциал окружности 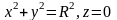массой Mв точке плотность в любой точке окружности пропорциональна расстоянию от этой точки до оси OX.

Параметризуем окружность: (см. рис. 9):

Тогда, как легко проверить,

Плотность линии в точке N(x,y)равна Найдем коэффициенты k> 0, для чего вычислим массу окружности:

откуда .

Поэтому, по формуле (3), потенциал в точке Pравен:

Для вычисления этого интеграла сделаем замену:

Тогда:

2. Криволинейный интеграл второго рода

2.1. Определение криволинейного интеграла второго рода.

В этом разделе мы познакомимся с еще одним типом криволинейных интегралов.

Начнем с определения ориентированной кривой в пространстве.

Определение 1. Кривую Г, определяемую уравнением

,

будем называть ориентированной кривой, если на ней задан порядок следования точек, а именно, точка следует за точкой , если радиус-вектор точки отвечает значению параметра 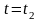большему, чем значение параметра радиус-вектора точки , т.е. .Точка Ас радиус-вектором называется началом кривой, а точка В с радиус-вектором – концом кривой (см. рис.1).

ПРИМЕР 1. Для окружности на плоскости OXY (см. рис. 10) радиус-векторы точек в параметрическом виде можно определить выражением:

, 0 ≤ t ≤ 2π.

Эта кривая – ориентированная: при возрастании параметра t от значения t = 0,

отвечающего точке A происходит движение соответствующей точки кривой против часовой стрелки до точки B (для которой t = 2π).

Рис.10. К примеру 1.

При построении разбиения Т в этом параграфе будем предполагать, что точки разбиения следуют друг за другом. Обозначим через координаты вектора .Пусть на кривой определены три непрерывные функции: P(x,y,z), Q(x,y,z) и R(x,y,z). Тогда можно считать, что на кривой Г задана вектор-функция

Составим три интегральные суммы:

1. 

б)

в)

(1)

Теперь можно дать определение криволинейного интеграла второго рода.

Определение 2. Пусть существуют пределы интегральных сумм (1) при бесконечном увеличении числа точек деления и бесконечном уменьшении длин векторов , причем эти пределы не зависят ни от способа разбиения кривой Г, ни от выбора точек на дугах:

а)

б)

в)

(2)

Тогда криволинейным интегралом второго рода, или криволинейный интеграл от векторной функции вдоль ориентированной кривой Г, называется сумма интегралов, определенных формулой (2):

(3)

(В левой части равенства (3) под интегралом стоит скалярное произведение вектора на вектор )

Определение 3. Если кривая Г замкнута, то криволинейный интеграл, определяемый формулой (3), называется циркуляцией вектора по контуру Г. Для циркуляции обычно используется обозначение

Как и в случае криволинейных интегралов первого рода, верна теорема:

Теорема 1. Если Г – кусочно-гладкая кривая и вектор имеет непрерывные на Г компоненты P(x,y,z), Q(x,y,z) и R(x,y,z), то криволинейные интегралы (2) и (3) существуют и определены однозначно. Используя формулу для дифференцирования сложной функции получаем еще одно утверждение:

Теорема 2. Если кривая Г задается векторным уравнением (1)п. 1.1, то интеграл (3) вычисляется по формуле:

Аналогичные формулы справедливы для каждого из интегралов (2).

Замечание. Криволинейный интеграл второго рода, в отличие от криволинейного интеграла первого рода, зависит от ориентации кривой.

При изменении ориентации (заданного направления движения по кривой) интегралы (2) – (4)меняют знак. Это связано с тем, что в определении криволинейного интеграла второго рода в интегральных суммах (1) значения координат Δxk, Δyk,Δzk меняют знак при изменении направления векторов на противоположное. В криволинейном интеграле первого рода изменения знака не происходит, поскольку в соответствующей интегральной сумме (2) из п. 1.1 величины Δsk– длины дуг разбиения, которые не изменяются при изменении направления обхода кривой.

ПРИМЕР 2 . Найти циркуляцию вектора вдоль контура в направлении возрастания параметра t(см. рис. 11).

Рис.11. К примеру 2.

Заметим сначала, что для точек, лежащих на контуре Г справедливы соотношения: и , т.е. кривая Г есть замкнутая линия пересечения цилиндра с плоскостью .

Если начать движение по кривой Г от точки A(2, 0, – 1) в которой значение параметра t равно 0, то при изменении параметра t до значения 2π, точка кривой вернется в исходную точку A. Используя теорему 2, можно записать:

ПРИМЕР 3.Найти модуль циркуляции вектора вдоль контура

(см. рис. 12).

Рис.12. К примеру 3.

Для точек (x, y, z), лежащих на контуре Г, можно записать: откуда, учитывая условие , получаем 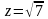. Поскольку для точек кривой Г выполнено соотношение , на ней можно ввести параметризацию: .

Поскольку в примере требуется найти модуль циркуляции, то направление обхода кривой не имеет значения (при его изменении на противоположный меняется знак всего криволинейного интеграла второго рода, а значит и циркуляции). Примем, что движение по кривой происходит в сторону увеличения параметра t. Применяя теорему 2, получим:

откуда модуль циркуляции равен

Замечание. Все определения и утверждения, сформулированные выше для пространственных кривых, справедливы и в случае плоских кривых. В соответствующих формулах нужно лишь убрать третью координату z(t).