1.2. Расчеты возвышения наружной рельсовой нити в кривой.

Перемещение экипажа в кривой складывается из двух движений: поступательного и вращательного вокруг точки, расположенной на продольной оси экипажа, называемой центром поворота.

Непрерывное вращение экипажа относительно центра поворота происходит под действием сил, возникающих в точках соприкосновения гребней колес направляющих осей с боковой гранью головки рельсов. Это направляющие силы.

При непрерывном повороте экипажа в кривой возникает центробежная сила J , равная произведению массы экипажа m на величину ускорения, и направленная в сторону от центра кривой (рисунок 1.3), определяется по формуле:

J = ; (1.6)

где V - скорость движения; R - радиус кривой.

Рисунок 1.3.- Расчетная схема для определения возвышения наружного рельса в кривых:

h- возвышение наружного рельса в кривой радиуса R; S₀- расстояние между осями рельсов (S₀= 1600); G- вес экипажа; J- центробежная сила; N, T- составляющие веса экипажа G; α- угол наклона полотна пути.

Для уменьшения величины центробежной силы и связанных с ней неблагоприятных последствий, в кривых участках пути устраивают возвышение наружного рельса.

Величина возвышения определяется по следующим формулам:

- для пассажирского поезда:

(1.7)

где - максимальная скорость пассажирского поезда,

R – радиус кривой, м.

- для потока поездов:

(1.8)

где - средневзвешенная скорость потока, определяется по формуле:

(1.9)

где n_i – число поездов

Q_i – масса поездов, т;

V_i – фактическая скорость движения поездов,

Из полученных по формулам 1.7 и 1.8 значений h принимается наибольшее, с округлением до 5 мм в большую сторону и сравнивается с максимальной величиной возвышения [h]=150мм.

Максимальная величина возвышения наружного рельса вычисляется по формуле 1.7 и 1.8 равняется h=100мм.

Так как расчетное возвышение меньше установленного максимального

возвышения ([h]=150мм), то для дальнейших расчетов принимаем h=100мм.

1.3. Проектирование переходных кривых.

Прямые и круговые кривые во избежание внезапного появления центробежной силы должны сопрягаться плавно с помощью переходных кривых. Основное назначение переходных кривых заключается в обеспечении плавного изменения центробежных сил при входе экипажей в круговую кривую и выходе из нее. На их протяжении осуществляют плавные отводы возвышения наружной рельсовой нити и уширения колеи в круговой кривой. Схема переходной кривой в увязке с отводом возвышения наружной рельсовой нити и изменением центробежной силы представлена на рисунке 1.4.

В качестве переходных кривых чаще всего используют радиоидальные спирали и реже - кубические параболы. У этих кривых кривизна K_x изменяется плавно, увеличиваясь пропорционально их длине l_x ,

K_x = 1/ρ_x = 1/C* l_x, (1.10)

где C - коэффициент пропорциональности, называемый параметром переходной кривой;

ρ_x - радиус кривизны.

Столь же плавно изменяется центробежное ускорение, а, следовательно, и центробежные силы, благодаря чему снижается их отрицательное воздействие на пассажиров, путь и подвижной состав.

Учитывая, что для конца переходной кривой l_x=l₀ и ρ_x=R, параметр переходной кривой определяется как:

C = R* l₀; (1.11)

Длина переходной кривой определяется по формуле:

(1.12)

где i – уклон отвода, %;

h – величина возвышения наружного рельса, мм.

Рисунок 1.4.- Схема переходной кривой: а- изменение возвышения наружной рельсовой нити над внутренней; б- план участка пути с переходной кривой (по оси пути); в- изменение центробежной силы.

Значение уклона отвода при скорости движения до 85 равняется i=1,4%.

Одним из основных элементов переходной кривой является коэффициент пропорциональности С, называемый параметром переходной кривой. Он определяется по формуле:

С = Rl₀; (1.13)

Определим его значение:

С = 350·80=28000 м².

Разбивка переходных кривых на местности обычно проводится со сдвижкой ранее намеченной круговой кривой внутрь (рисунок 1.5) на величину Р.

Рисунок 1.5.- Схема разбивки переходных кривых методом сдвижки круговой кривой внутрь.

Определим угол поворота φ₀ на протяжении переходной кривой по формуле:

. (1.14)

Тогда:

рад; φ₀ = 6,549^о.

Проверим возможность разбивки переходной кривой по зависимостям:

β>2φ₀ и L_кк=R(β–2φ₀) ≥ 30 м, (1.15)

где β – угол поворота трассы;

L_кк – длина круговой кривой, м.

Угол поворота трассы согласно заданию:

β = 47^о = 0,8203 рад.

Найдем длину круговой кривой по формуле:

L_кк = R(β − 2φ₀). (1.16)

Тогда:

L_кк=350(0,8203–2·0,1143)= 207,095 м.

Проверим:

β>2φ₀; 0,8203>2·0,1143; 0,8203>0,2286;

L_кк ≥ 30 м; 207,095 > 30 м.

Проверки выполняются, разбивка переходных кривых возможна.

Определим вид переходной кривой и координаты для ее разбивки в прямоугольной системе. Прежде всего, проверим возможность применения в качестве переходной кривой кубической параболы из следующей формулы

(1.17)

Найдем численное значение правой части этого выражения:

1,602·28000^5/9=473,485 м.

Условие (1.17) выполняется (350 < 473,485), и для разбивки переходной кривой принимаем кубическую параболу с определением координат по формуле:

, (1.18)

где l_i – принимать равным 10, 20, 30…l₀.

Расчет сведем в таблицу 1.3.

Таблица 1.3. – Координаты переходной кривой по кубической параболе.

li	, м	, м
10	10,000	0,00595
20	20,000	0,04762
30	30,000	0,1607
40	39,997	0,38093
50	49,99	0,74394

60	59,975	1,28533
70	69,946	2,04055
80	79,89	3,04478

По результатам расчетов построим график (Приложение 1).

Сдвижка р, м, круговой кривой внутрь определяется по формуле:

p = y_к− R·(1−cosφ₀) (1.19)

где y_к – координата у конца переходной кривой, м.

p = 3,04478−350·(1−cos 6,549) = 0,76092 м.

Расстояние m₀, м, от начала переходной кривой до первоначального положения тангенсного столбика определяется по формуле:

, (1.20)

где m – расстояние от начала переходной кривой до нового положения тангенсного столбика, м, определяемое по формуле:

m = x_к−Rsinφ₀, (1.21)

где x_к – координата х конца переходной кривой, м.

Тогда:

m = 79,89−350·sin 6,549 = 39,971м;

м.

Полная длина кривой L_кр, м, (с переходными кривыми) определяется по формуле:

L_кр = 2l₀+R(β−2φ₀); (1.22)

L_кр = 2·80+350(0,8203−2·0,1143) = 367,095 м.

Суммарный тангенс новой кривой , м, определяется по формуле:

; (1.23)

м.

Суммарная биссектриса Б, м, определяется по следующей формуле:

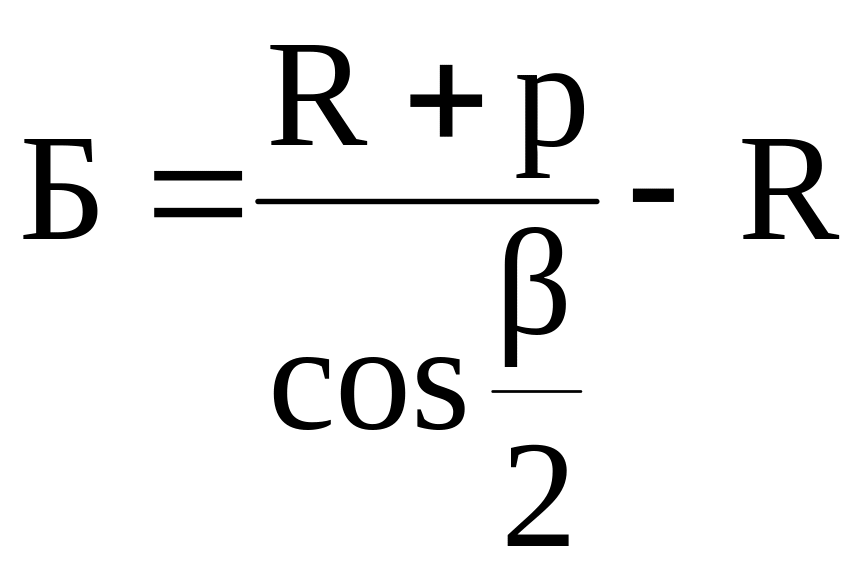; (1.24)

м.

Домер Д, м, определим по формуле:

Д = 2T_кр−L_кр; (1.25)

Д = 2·192,486 – 367,095 = 17,877 м.

Разбивку круговой и переходной кривой на местности производим геодезическим методо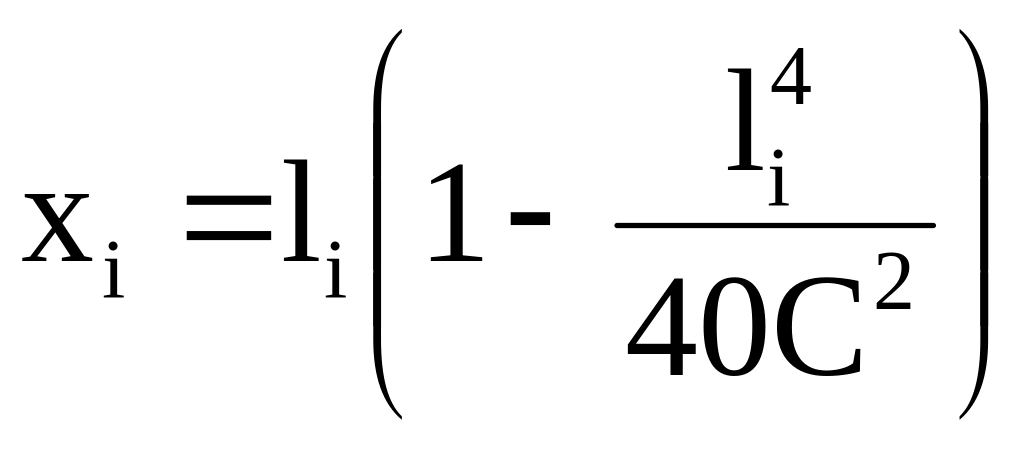м.