
- •Задания 14: исследование функций с помощью производной (точки экстремума, наибольшее (наименьшее) значения функции) Функция задана формулой
- •Производная задана графиком
- •Приемы быстрого решения заданий 14 без использования производной
- •1. Тригонометрические функции вида
- •2. Тригонометрические функции вида
- •При определении х тригонометрических функций вида
- •6. Функции вида , где а - числа
- •8. Применение свойства корней
Задания 14: исследование функций с помощью производной (точки экстремума, наибольшее (наименьшее) значения функции) Функция задана формулой
Правило отыскания наибольшего и наименьшего значений f: чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Критические точки – внутренние точки области, в которых ее производная равна нулю или не существует.
Правила вычисления производных: Таблица производных
|
|
х´= 1 |
|
Применяя изложенный выше метод поиска наибольшего и наименьшего значений функции, будем следовать алгоритму:
1) найдем производную данной функции;
2) приравняем ее к нулю;
3) выберем критические точки, лежащие внутри отрезка;
4) найдем значение функции в этих точках и на концах отрезка;
5) из полученных чисел выберем наибольшее или наименьшее.
Пример 1.
Задание 14.Найти наименьшее значение
функции
|
Признак максимума и минимума
функции: если в точке![]() производная
меняет знак с «+» на «-», то
есть точка максимума, с «-» на
«+», то
– точка минимума.
производная
меняет знак с «+» на «-», то
есть точка максимума, с «-» на
«+», то
– точка минимума.
При решении практических задач на нахождение точки максимума или минимума функции следуем такому алгоритму:
1) найдем область определения данной функции;
2) найдем производную данной функции;
3) приравняем ее к нулю;
4) найдем промежутки знакопостоянства функции;
5) найдем точку максимума или минимума.
Пример 2.
Производная задана графиком
1) На тех промежутках, где график расположен выше оси абсцисс (т.е. производная положительная), функция возрастает.
2) На тех промежутках, где график расположен ниже оси абсцисс (т.е. производная отрицательная), функция убывает.
3) Точки, в которых график производной пересекает ось абсцисс (т.е. точки, в которых производная меняет знак), являются точками экстремума.
Точки экстремума – точки максимума
![]() и
минимума
и
минимума
![]() .
.
Пример 3.
Задание 14. Функция
межутке (-5;5). На рисунке изображен
график ее производной
точку
,
в которой функция
принимает наибольшее значение.
|
Приемы быстрого решения заданий 14 без использования производной
При нахождении наибольшего (наименьшего) значения функции можно найти приемы быстрого решения без использования производной для большинства заданий 14. При этом учитывается, например:
а) ответ без округления должен быть целым числом или конечной десятичной дробью;
б) какое значение нужно найти: наибольшее или наименьшее;
в) числа π, е – иррациональные;
г)
![]() ,
,
![]() ;
;
д) технология составления формул;
е) значение х обязательно принадлежит данному отрезку;
ж) действия над рациональными числами;
з) чтобы число обязательно извлекалось из-под корня целым числом и т.д.
Показано несколько приемов быстрого решения заданий 14 на нахождение наибольшего (наименьшего) значения функции.

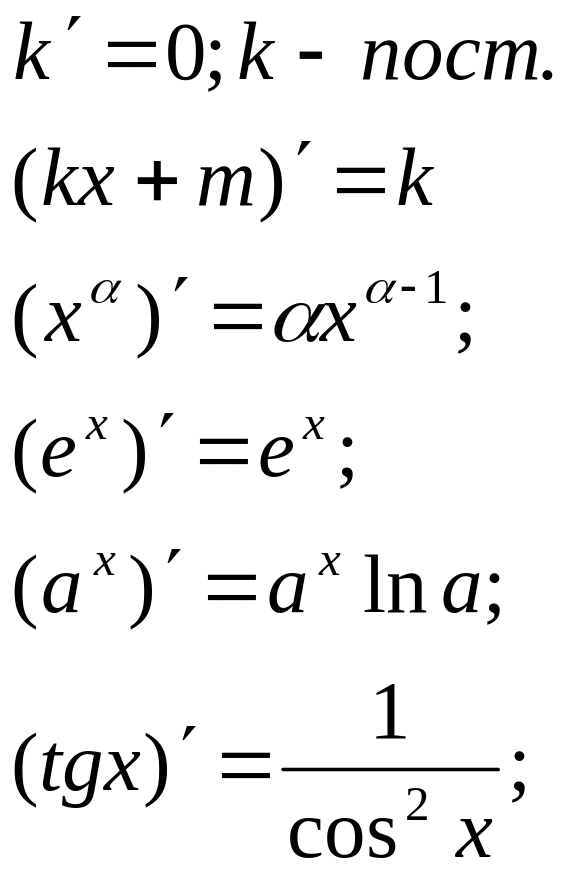
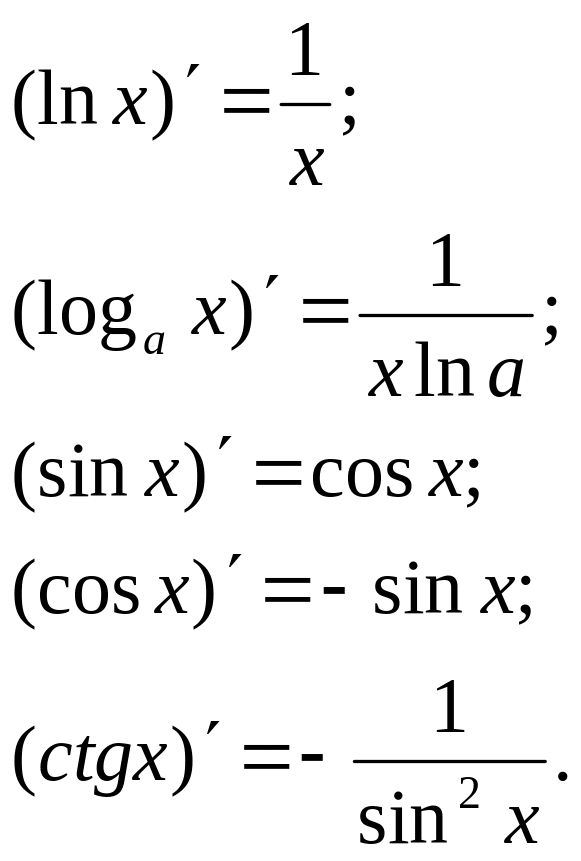
 у
у