1.3. Расчетные формулы для вычисления температуры в конструкции при двустороннем обогреве

1. . При параллельном направлении тепловых потоков

При расчете пределов огнестойкости стержневых конструкций определяют температуру внутри конструкции при обогреве с двух противоположных направлений, в частности в центре (середине) поперечного сечения конструкции

Расчетная формула для определения температуры выведена Яковлевым путем преобразования формулы Фурье (1.7).

t_x, = 1250 - (1250 - t_н)[erf + erf - 1], (1.18)

где x_i - расстояние от центральной оси (у) конструкции до расчетной точки, м;

 - толщина конструкции, м;

 = 1- ; (1.19)

F₀ - критерий Фурье

F₀= . (1.20)

Величина в скобках (1.18) представляет собой относительную избыточную температуру - 

[erf + erf - 1] = , (1.21)

которую можно определить по номограмме рис. 22 [3] (рис 4.2 [6]) в зависимости от величин  и F₀.

С учетом этого формулу (1.18) можно представить в виде

t_x, = 1250 - (1250 - t_н). (1.22)

Тогда температура в центре сечения (в точке пересечения координат: x=0) будет определятся по формуле

t_x=0, = 1250 - (1250 - t_н)_ц . (1.23)

_ц определяется по таблице 1.6 [5], либо по таблице 7 [3] (таблица 4.5 [6]) в зависимости от величины .

2. . При взаимно перпендикулярном направлении тепловых потоков

При нагреве балок, колонн, ферм и др. стержневых конструкций, обогреваемых с 3-х или 4-х сторон, имеет место двухмерное температурное поле, в котором тепловые потоки взаимно перпендикулярны в точке определения температуры.

Расчет температур в точках для практики с достаточной точностью выполняется по формуле, полученной из известных в теории теплопроводности соотношений разностей температур

, (1.24)

где t_в - температура в огневой камере печи при стандартном температурном режиме в момент времени ;

t_н - начальная температура конструкции (до пожара t_н= 20⁰С);

t_x, - температура в заданной точке внутри конструкции с координатой x при одностороннем обогреве в направлении оси х в момент времени ;

t_y, - то же но по оси y;

t_x,y, - то же (в точке с координатами х,у).

С учетом (1.24), предварительно вычислив температуры t_x, и t_y,, которые бы имела заданная точка поперечного сечения конструкции при обогреве с одной стороны (х или y) по формуле

t_x,y,=t_в - (1.25)

можно вычислить температуру при обогреве в двух взаимно перпендикулярных направлениях.

3. . Расчетные формулы для вычисления размеров «ядра» поперечного сечения конструкции при её обогреве с четырёх сторон

При решении теплотехнической части задачи огнестойкости стержневых конструкций по 3-й расчетной схеме возникает необходимость вычисления размеров так называемого несущего нагрузку «ядра» поперечного сечения конструкции в различные моменты времени при стандартном температурном режиме.

Условно считается, что прочность бетона в «ядре» равна первоначальной.

Температуру на границе «ядра» условно называют «критической» - для упрощения расчета (это понятие не идентично с «критической температурой» для арматуры; строго говоря, нельзя говорить в этом случае о «критической температуре бетона», т.к. этот материал расположен практически по всему поперечному сечению железобетонных конструкций и он прогревается неравномерно).

В теплотехнической части расчета предела огнестойкости колонны возникает необходимость вычисления размеров «ядра» ее поперечного сечения.

Толщину слоя _t,y прогретого выше t_сr в направлении y вычисляют следующим образом:

t_y,=1250 - (1250 - t_н)erf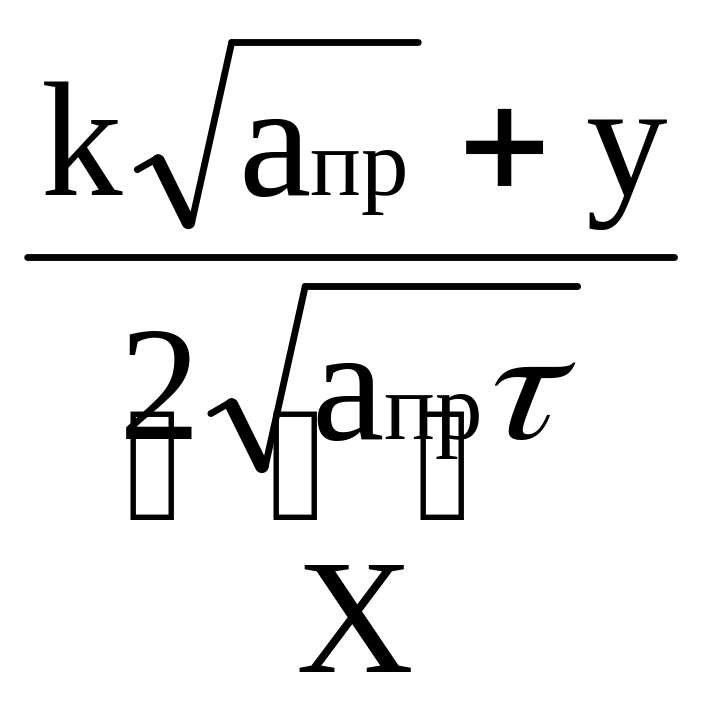 , (1.26)

откуда заменой y на _t,y

_t,y = (2X - k) , (1.27)

где X - аргумент функции Гаусса (Крампа), определяется, например, по таблице 1.4 [5], предварительно вычислив значение функции по формуле

erf X = , (1.28)

где t_б,сr= t_y, - для бетона на гранитном щебне – 650 ⁰С, на известняковом – 750 ⁰С.

При обогреве конструкции с четырех сторон «ширину» ядра поперечного сечения вычисляют по формуле

_я,y= (0,5b_y+k )(1-_y), (1.29)

_y - определяют по графикам номограмм - рис. 22 [3] в зависимости от величины относительной температуры _y в точке y при обогреве в одном направлении и критерия Фурье F_0y;

_y - вычисляют по формуле

_y= , (1.30)

где t_x=0, - температура в центре поперечного сечения конструкции (колонны), ⁰С определяют по формуле

t_x=0,=1250 - (1250 - t_н)_ц , (1.31)

_ц - определяют по таблице 1.6 [5] и др. в зависимости от , а критерий Фурье F_0y= . (1.32)

Аналогично поступают в направлении оси - х.