курсовик (12)

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Информатика и вычислительная техника»

КУРСОВОЙ ПРОЕКТ

по дисциплине «Основы теории управления»

Выполнил:

студент гр.

подпись, дата

Проверил:

доцент Юдин В.А.

подпись, дата

Омск 2005

Содержание

Задание на проектирование 3

Задание на проектирование 3

1 Передаточная функция разомкнутой системы 4

1 Передаточная функция разомкнутой системы 4

2 Передаточная функция замкнутой системы 5

2 Передаточная функция замкнутой системы 5

3 Передаточная функция по ошибке 6

3 Передаточная функция по ошибке 6

4 Дифференциальное уравнение замкнутой системы 7

4 Дифференциальное уравнение замкнутой системы 7

5 Характеристическое уравнение замкнутой системы 8

5 Характеристическое уравнение замкнутой системы 8

6 Дифференциальное уравнение для ошибки 9

6 Дифференциальное уравнение для ошибки 9

7 Коэффициенты ошибок 10

7 Коэффициенты ошибок 10

8 Схема САУ и коэффициенты модели 11

8 Схема САУ и коэффициенты модели 11

8.1 Модель идеального интегрирующего звена 11

8.2 Модель реального дифференцирующего звена 11

8.3 Модель инерционного звена 11

9 Параметры корректирующего устройства, обеспечивающие минимум интегральной оценки 13

9 Параметры корректирующего устройства, обеспечивающие минимум интегральной оценки 13

10 Переходный процесс и начальные показатели переходного процесса 14

10 Переходный процесс и начальные показатели переходного процесса 14

Задание на проектирование

Вариант-16

Рисунок 1 – Структурная схема САУ

k₁ = 10

k₂ – Выбрать из минимума интегральной оценки

k₃ = 5

k₄ = 1,5

T₁ - Выбрать из минимума интегральной оценки

T₂ = 0,1

T₃ = 0,15

По заданной структурной схеме САУ (рис. 1) найти:

1. Передаточную функцию разомкнутой системы W(p);

2. Передаточную функцию замкнутой системы Ф(p);

3. Передаточную функцию ошибки W_x(p);

4. Дифференциальное уравнение замкнутой системы;

5. Характеристическое уравнение замкнутой системы;

6. Дифференциальное уравнение ошибки;

7. Найти первые два коэффициента ошибки С₀, С₁

8. Пользуясь структурным методом моделирования, составить схему для модели САУ на ПК и рассчитать коэффициенты модели.

9. Выбрать параметры корректирующего устройства, обеспечивающие минимум интегральной оценки

10. Построить переходный процесс для найденных параметров корректирующего устройства и определить показатели переходного процесса.

1 Передаточная функция разомкнутой системы

2 Передаточная функция замкнутой системы

3 Передаточная функция по ошибке

4 Дифференциальное уравнение замкнутой системы

5 Характеристическое уравнение замкнутой системы

6 Дифференциальное уравнение для ошибки

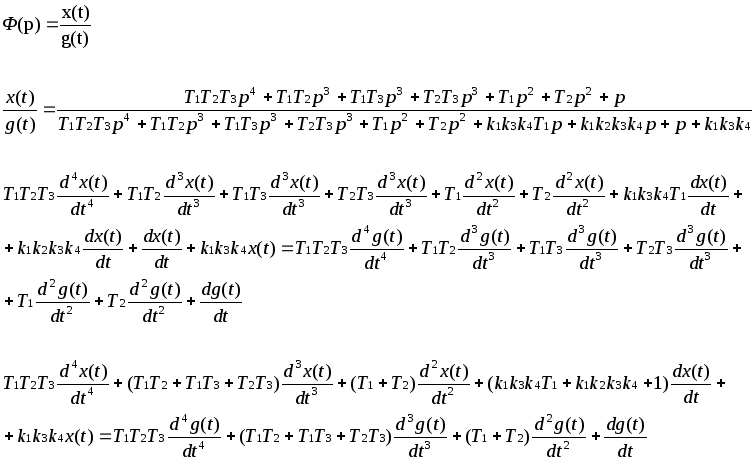
7 Коэффициенты ошибок

Чтобы получить коэффициенты ошибки, разложим передаточную функцию ошибки системы в степенной ряд:

,

где с₀, с₁, с₂ …— коэффициенты ошибок.

c₀ = 0

8 Схема САУ и коэффициенты модели

8.1 Модель идеального интегрирующего звена

8.2 Модель реального дифференцирующего звена

8.3 Модель инерционного звена

С учетом произведенных расчетов, схема для моделирования САУ на ПК имеет вид:

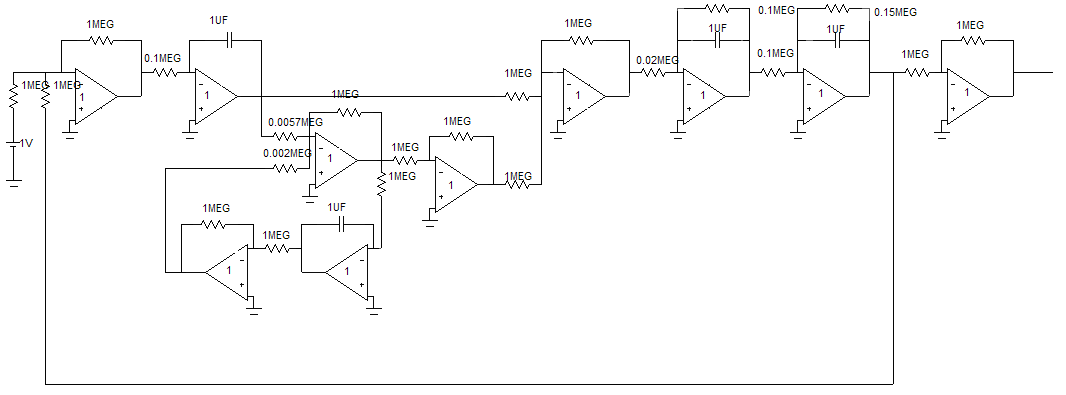
Рисунок 2 - Схема для моделирования САУ на ПК

9 Параметры корректирующего устройства, обеспечивающие минимум интегральной оценки

Выберем параметры корректирующих устройств исходя из минимума интегральной оценки.

Будем использовать интегральную оценку вида: .

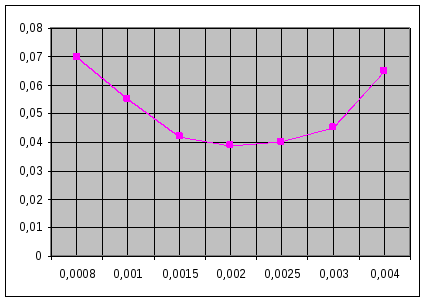
T1	I(t)	Рисунок 3 – Зависимость I от T1
0,0008	0,07
0,001	0,055
0,0015	0,042
0,002	0,039
0,0025	0,04
0,003	0,045
0,004	0,065

k2	I(t)	Рисунок 4 – Зависимость I от k2
0,1	0,0665
0,15	0,046
0,2	0,0405
0,25	0,0385
0,3	0,0375
0,35	0,037
0,4	0,0375
0,45	0,038
0,5	0,0385

По графикам видно, что минимум интегральной оценки достигается при:

T₁ = 0,002

k₂ = 0,35

10 Переходный процесс и начальные показатели переходного процесса

Рисунок 5 – График переходного процесса

Y_max = 1.65

Y_уст = 1

 =

t_п = 0.5 с при E = 10%

14