курсовик (2)
.doc
Министерство образования и науки РФ.
Омский Государственный Технический Университет.
Кафедра ИВТ.
Курсовая работа по дисциплине:
Основы теории управления.
Выполнил студент группы В-233:
Егиазарян А.С.
Проверил доцент:
Юдин В.А.
г. Омск - 2004
Задание:
По заданной структурной схеме САУ найти:
-
Передаточную функцию разомкнутой системы W(p).
-
Передаточную функцию замкнутой системы Ф(р).
-
Передаточную функцию ошибки Wx(p).
-
Записать дифференциальное уравнение замкнутой системы.
-
Записать характеристическое уравнение замкнутой системы.
-
Записать дифференциальное уравнение для ошибки.
-
Найти первые два коэффициента ошибки С0 и С1.
-
Пользуясь структурным методом моделирования, составить схему для моделирования САУ на ЭВМ и рассчитать коэффициенты модели. После составления схему показать преподавателю и получить коэффициенты для моделирования.
-
Выбрать параметры корректирующего устройства, обеспечивающие минимум интегральной оценки и для найденных параметров построить переходный процесс.
W1=
;
W6=
1+(
);
W7=
;
W5=
;
Передаточная функция разомкнутой системы.
W(p)
=W1(p)*W6(p)*W7(p)*W5(p)=
(1+
)(
)(
)
=
=
;
Передаточная функция замкнутой системы.
Ф(р) =
=
Передаточная функция ошибки.
Wx(p)=
Дифференциальное уравнение для замкнутой системы.
Ф(р)=
| p=
|
T1T2T3
+
(T1T3+T2T3+T1T2T3K3+T1T2)
+
(T1T3K3+T2T3K3+T1+T2+
+T1T2K3)
+
(T1K3+T2K3+T3K3+1)
+
(K1K2K4+K1T2K4+K3)
+
+K1K4Xвых(t)
=
(K1K4T2
+ K1K2K4)
+ K1K4Xвх(t).
Характеристическое уравнение замкнутой системы.
Для получения характеристического уравнения замкнутой системы необходимо сложить числитель и знаменатель передаточной функции разомкнутой системы и приравнять полученное выражение к 0.
W(p)=
; Q(p) + R(p) = 0.
T1T2T3p5 + (T1T3+T2T3+T1T2T3K3+T1T2)p4 + (T1T3K3+T2T3K3+T1+T2+T1T2K3)p3 +
+ (T1K3+T2K3+T3K3+1) p2 + (K1K2K4+K1T2K4+K3)p + K1K4.
Дифференциальное уравнение для ошибки.
T1T2T3
+
(T1T3+T2T3+T1T2T3K3+T1T2)
+
(T1T3K3+T2T3K3+T1+T2+
+T1T2K3)
+
(T1K3+T2K3+T3K3+1)
+
(K1K2K4+K1T2K4+K3)
+
+K1K4Xвых(t)
= T1T2T3
+
(T1T3+T2T3+T1T2T3K3+T1T2)
+
(T1T3K3+T2T3K3+T1+T2+T1T2K3)
+
(T1K3+T2K3+T3K3+1)
+
K3
;
Определение коэффициентов ошибки.
Для определения коэффициентов ошибки разделим в передаточной функции ошибки числитель на знаменатель.
Свободных членов нет – С0=0.
Коэффициент при
p1
– С1
=
;
Определение параметров R и C.
Для звена
:
R1= 1 MEG;
K1=R2/R1; C = 0.1/5 = 0.02NF;
T1= R2C;
Для звена
:
R1= 1 MEG;
R2= K2 – посчитано из минимума интегральной оценки.
Для звена
:
R1= 1 MEG;
K4=R2/R1; C = 0.15/5 = 0.03NF;
T3= R2C;
K3= 0.5 - фиксированное.
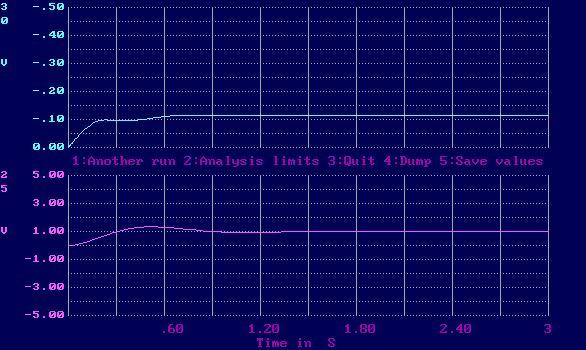
Переходный процесс и минимум интегральной оценки.
Коэффициенты: K1= 5
T1= 0.1c
K4= 5
T3= 0.15c
K3 = 0.5 – фиксированное значение.
K2= 0.1 – из минимума интегральной оценки.
T2= 0.1.
