курсовик (3)

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

Омский Государственный Технический Университет

Кафедра: «Информатика и вычислительная техника»

Курсовой проект по дисциплине:

«Основы теории управления»

Выполнил: студент группы ИВТ-235

Ю.В. Никифорова

Подпись____________

Число______________

Проверил доцент

В.А.Юдин.

Омск 2006г.

Оглавление

Передаточная функция разомкнутой системы 5

Передаточная функция замкнутой системы 5

Передаточная функция ошибки 6

Дифференциальное уравнение замкнутой системы 6

Характеристическое уравнение замкнутой системы 6

Дифференциальное уравнение для ошибки 7

Первые два коэффициента ошибки С0, С1 7

Схема для моделирования САУ на ПК и расчет коэффициентов. 8

8

Минимум интегральной оценки. 10

10

Переходный процесс. 11

Задание

По заданной структурной схеме САУ (рисунок 1)

1. Передаточную функцию разомкнутой системы W(p);

2. Передаточную функцию замкнутой системы Ф(p);

3. Передаточную функцию ошибки W_x(p);

4. Дифференциальное уравнение замкнутой системы;

5. Характеристическое уравнение замкнутой системы;

6. Дифференциальное уравнение ошибки;

7. Найти первые два коэффициента ошибки С₀, С₁

8. Пользуясь структурным методом моделирования, составить схему для модели САУ на ЭВМ и рассчитать коэффициенты модели.

9. Выбрать параметры корректирующего устройства k_oc обеспечивающие минимум интегральной оценки.

10. Построить переходный процесс для выборных параметров и определить качественные параметры переходного процесса.

Рисунок1 – Структурная схема САУ

Коэффициенты передаточных функций:

k_oc – выбрать из минимума интегральной оценки.

Передаточная функция разомкнутой системы

При нахождении передаточной функции разомкнутой системы воспользуемся формулами для передаточных функций последовательно и параллельно соединенных звеньев:

=

.

Передаточная функция замкнутой системы

Используя формулу для нахождения передаточной функции замкнутой системы , где W(p) передаточная функция разомкнутой системы, получаем

Передаточная функция ошибки

Используя ранее найденное значение передаточной функции разомкнутой системы, найдем передаточную функцию ошибки

Дифференциальное уравнение замкнутой системы

Характеристическое уравнение замкнутой системы

Чтобы получить характеристическое уравнение замкнутой системы необходимо сложить числитель и знаменатель передаточной функции разомкнутой системы и приравнять к нулю.

Дифференциальное уравнение для ошибки

Первые два коэффициента ошибки С₀, С₁

Схема для моделирования САУ на ПК и расчет коэффициентов.

Рисунок 2 – Схема для моделирования САУ на ПК

Расчет коэффициентов:

1) Модель элемента сравнения сигналов.

Модель сравнения сигналов можно представить в виде суммирующего операционного усилителя. Так как не нужно усиливать сигнал, то зададим значения резисторов 1MОм.

2) Модель идеального интегрирующего звена.

K2=0.5 Зададим R=1 MОм, тогда С=2 мкФ.

3) Модель колебательного звена.

K1=10, T1=0,05, E=0,5.

Зададим С=T²=0, 0025 мкФ, тогда ; ;

5) Модель инерционного звена:

Для инерционного звена задаем значение С=1 мкФ, тогда R₂=0.12 МОм, т.к. k₄=5, то R₁=0,6 MOм.

Минимум интегральной оценки.

I(Koc)	Koc
0,53	1,1
0,43	1
0,35	0,9
0,3	0,8
0,23	0,7
0,25	0,6
0,31	0,5

Функция I(k_oc) принимает минимальное значение при k_oc=0.7

Переходный процесс.

Построим переходный процесс для выборных параметров корректирующего устройства, удовлетворяющих минимуму интегральной оценки.

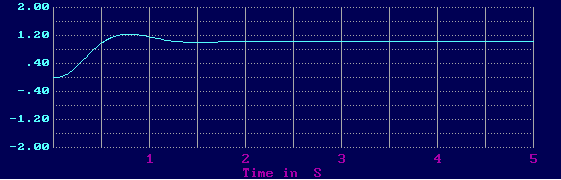
Качественные параметры переходного процесса.

11