курсовик (27)

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

«Омский государственный технический университет»

Кафедра информатики и вычислительной техники

Специальность 230101

«Вычислительные машины,комплексы,системы и сети»

 

 

 

 

 

 

 

 

 

 

 

 

Курсовой проект по дисциплине «Основы теории управления»

Вариант №3

 

 

 

 

 

Выполнил:

студент группы ИВТ-318

Кошевой Н.В

  Дата, подпись: _____________

 

                                                                                 Проверил:                                доцент Суриков Р.О.

  Дата, подпись:

  ______________        

 

 

Омск 2010

Вариант №3

Структурная схема САУ:

 

 

Вариант №17:

 

 

 

 

 

 

 

 

 

 Исходные данные для моделирования:

k₁=10 c^-1 T=0,12 с. =0,5

k₂= 0.1 c^-1 Т₁=0,1 с.

k₃=10 c^-1 Т₂=0,08 c.

k_ос и T_ос вычисляем с помощью минимальной интегральной оценки.

 

По заданной структурной схеме САУ найти:

 

1. Передаточную функцию разомкнутой системы W(p);

2. Передаточную функцию замкнутой системы Ф(p);

3. Передаточную функцию ошибки W_x(p);

4. Записать дифференциальное уравнение замкнутой системы;

5. Записать характеристическое уравнение замкнутой системы;

6. Записать дифференциальное уравнение ошибки;

7. Найти первые два коэффициента ошибки С₀, С1

8. Пользуясь структурным методом моделирования, составить схему для модели САУ на ЭВМ и рассчитать коэффициенты модели.

9. Выбрать параметры корректирующего устройства обеспечивающей минимум интегральной оценки и построить переходный процесс для выборных параметров.

1) Передаточная функция разомкнутой системы W(p):

2) Передаточная функция замкнутой системы Ф(р):

3) Передаточная функция ошибки W_x(p):

4) Дифференциальное уравнение замкнутой системы:

5) Характеристическое уравнение замкнутой системы:

6) Дифференциальное уравнение для ошибки:

7) Коэффициенты ошибки c₀ и c₁:

Поделив числитель Wx(p) на знаменатель Wx(p), получим:

с₀=0 с₁==0,025

8) Расчет элементов типовых звеньев:

Колебательное звено:

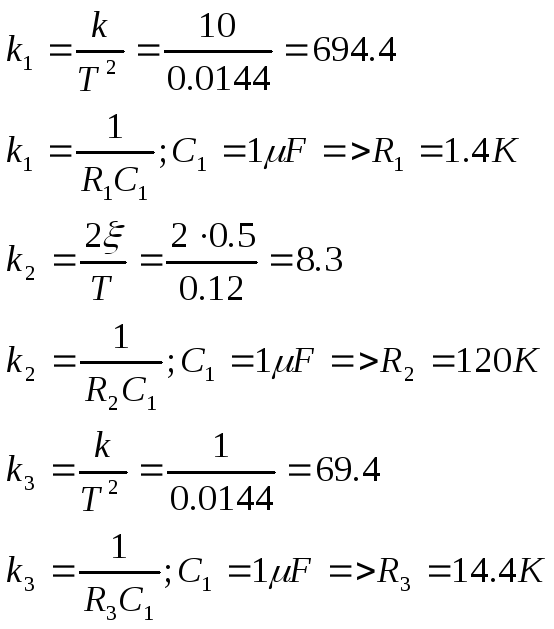
Инерционное звено с замедлением:

Приняв R1=1M, получим:

Инерционное звено:

Приняв R1=1M, получим:

Минимум интегральной оценки:

k_min=2.8 I_min= 0.129

T_min=0.028 I_min=0.129

Исходя из k_min и T_min рассчитаем дифференцирующее звено гибкой инерционной связи:

Приняв R₃=1М, получим:

Приняв k₃=1, получим:

Схема САУ:

График переходного процесса САУ:

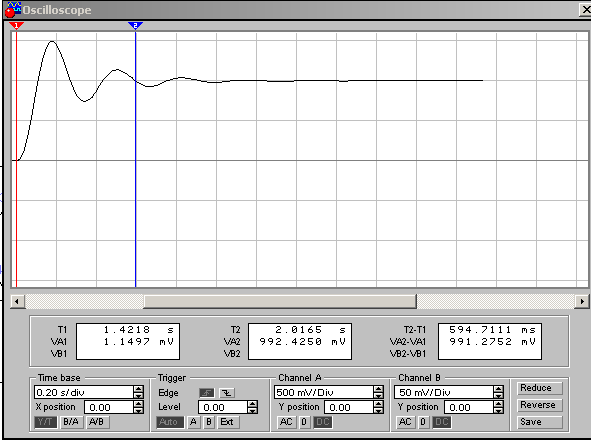
Для определения качественных параметров переходного процесса воспользуемся формулой:

 

Подставляя полученные результаты, получаем: