Дисциплина «Теория вероятностей и математическая статистика»

1. События и их вероятности. Правила сложения событий.

События называются несовместными (независимыми), если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Классический пример: при бросании игральной кости (кубика) может выпасть только единица, либо только двойка, либо только тройка и т.д. Каждое из этих событий происходит независимо от  других и совершение одного из них исключает совершение другого (в одном опыте).

О сумме вероятностей

Если происходят независимые события, то вероятность таких событий равна сумме вероятностей этих событий:

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же опыте.

Пример. Поступление в магазин одного вида товара — событие  . Поступление второго вида товара — событие  . Поступить эти товары могут и одновременно. Поэтому   и  - совместные события.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

P(A+B) = P(A) + P(B) — P(AB)

Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.

Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.

События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров. Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного.

2. Независимые события и правила умножения вероятностей. Формула полной вероятности.

События называются несовместными (независимыми), если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Классический пример: при бросании игральной кости (кубика) может выпасть только единица, либо только двойка, либо только тройка и т.д. Каждое из этих событий происходит независимо от  других и совершение одного из них исключает совершение другого (в одном опыте).

Об умножении вероятностей

Пусть происходят два несовместных события А и В, их вероятности   соответственно равны Р(А) и Р(В). Тогда вероятность совершения событий А и В одновременно равна произведению вероятностей. Вычисляется по формуле:

Пример с той же игральной костью:

Бросаем игральную кость два раза. Какова вероятность выпадения двух шестёрок?

Вероятность выпадения шестёрки первый раз равна 1/6. Во второй раз так же равна  1/6. Оба эти события несовместные (независимые). Вероятность выпадения шестёрки в первый раз и во второй раз равна произведению:

Говоря простым языком: когда происходит событие, и ПРИ ЭТОМ происходит(ят) другое (другие), то вероятности этих событий перемножаются.

Предположим, что событие   может осуществляться только с одним из несовместных событий  . Например, в магазин поступает одна и та же продукция от трех предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие  ). Здесь события  — это выбор изделия из продукции соответствующего предприятия.

В этом случае вероятность события   можно рассматривать как сумму произведений событий

По теореме сложения вероятностей несовместных событий получаем

Используя теорему умножения вероятностей, находим

 (3.1)

Формула (3.1) носит название формулы полной вероятности.

3. Случайные величины и законы их распределения.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.

 Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать.

Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы.

Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х₁, х₂, ..., х_n с соответствующими им вероятностями р₁, р₂, ..., р_n

Математическое ожидание

Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин

Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:

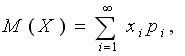
Свойство 1. Мат. ожидание постоянной равно этой постоянной.

Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:

Из этого свойства следует следствие:

Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:

 

Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Yравно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.

Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)

Дисперсия.

Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:

D[Х]=M[X-M(X)]²

Свойство 1. Дисперсия постоянной величины равна нулю.

Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:

D(cX) = c²D(X)

Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:

D(X+Y) = D(X) + D(Y), от сюда следствие:

если х₁, х₂, ..., х_n  - случайные величины, каждая из которых независима от суммы остальных, то

D(X₁+X₂+...+X_n) = D(X₁) + D(X₂)+...+D(X_n).

Моментом k-порядка называется математическое ожидание k-й степени отклонения случайнойвеличины Х от некоторой постоянной с.

Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.

Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:

где p^n - вероятность того, что при n испытаниях событие А наступит n раз;

qⁿ - вероятность того, что при n испытаниях событие А не наступит ни разу;

- вероятность того, что при n испытаниях событие А наступит m раз, а событие Āнаступит n-m раз;

- число сочетаний (комбинаций) появления события А и Ā.

Числовые характеристики биноминального распределения:

М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;

D(m)=npq - дисперсия частоты появления события. А;

- среднее квадратическое отклонение частоты

Нормальный закон распределение

 

Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна

,

где m - математическое ожидание случайной величины;

σ² - дисперсия случайной величины, характеристика рассеяния значений случайной величины около математического ожидания.

Условием возникновения нормального распределения являются формирование признака как суммы большого числа взаимно независимых слагаемых, ни одно из которых не характеризуется исключительно большой по сравнению с другими дисперсиями.

Нормальное распределение является предельным, к нему приближаются другие распределения.

Математическое ожидание случайной величины Х. распределено по нормальному закону, равно

m_x = m, а дисперсия D_x = σ².

Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервале (α, β) выражается формулой

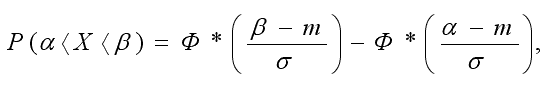
где  - табулированная функция

Закон Пуассона

Событие называются редкими, когда вероятность события р или противоположного ему q близка к нулю. При большом числе испытаний (n), но небольшой величине произведения числа испытаний на вероятность (np),

которое  меньше 10, вероятности полученные по формуле Лапласа

недостаточно близки к их истинным значениям. тогда применяют другую асимптотическую формулу

 Пуассона.

Теорема. Если вероятность р наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, произведение np = λ, то вероятностьР_n(m) того, что в n независимых испытаниях события А наступит m раз, приближенно равна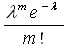 , т.е.

4. Статистические наблюдения и сводка.

Статистическое наблюдение – это первая стадия всякого статистического исследования, представляющая собой научно организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни, и сбор полученных на основе этого учета массовых данных.

Однако не всякий сбор сведений является статистическим наблюдением. О статистическом наблюдении можно говорить лишь тогда, когда, во-первых, обеспечивается регистрация устанавливаемых фактов в специальных учетных документах и, во-вторых, изучаются статистические закономерности, т.е. такие, которые проявляются только в массовом процессе, в большом числе единиц какой-то совокупности. Поэтому статистическое наблюдение должно быть планомерным, массовым и систематическим.

К статистическому наблюдению предъявляются следующие требования: 1) полноты и практической ценности статистических данных; 2) достоверности и точности данных; 3) их единообразия и сопоставимости.

Различают следующие виды наблюдения:

В зависимости от охвата единиц совокупности:

1. Сплошное наблюдение – регистрации подлежат все единицы изучаемой совокупности (перепись населения).

2. Несплошное наблюдение охватывает определённую часть изучаемой совокупности и в свою очередь подразделяется на:

• Выборочное наблюдение, кода обследованию подвергается отобранная случайным образом часть единиц совокупности, а полученные результаты распространяются на всю совокупность.

• Наблюдение основного массива, когда обследованию подвергается  основной массив – та часть единиц, которая вносит наибольший вклад в изучаемое явление.

• Монографическое наблюдение глубоко и всесторонне характеризует отдельные единицы совокупности. При этом не ставится цель охарактеризовать всю совокупность.

По времени регистрации наблюдения:

1. Непрерывное (текущее) наблюдение ведется систематически, постоянно, непрерывно, осуществляется путём непрерывной регистрации фактов по мере их возникновения.

2. Прерывное наблюдение производится либо регулярно через равные промежутки времени, либо по мере надобности и подразделяется на:

• Периодическое, при котором регистрация проводится через определенные, обычно одинаковые промежутки времени.

• Единовременное, которое поводится один раз для решения какой-либо задачи или повторяется по мере надобности.

Собранный в процессе статистического наблюдения материал нуждается в определенной обработке, сведении разрозненных данных воедино. Научно организованная обработка материалов наблюдения (по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой.

Сводка представляет собой второй этап статистического исследования. Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности.

Статистическая сводка осуществляется по программе, которая должна разрабатываться еще до сбора статистических данных, практически одновременно с составлением плана и программы статистического наблюдения. Программа сводки включает определение групп и подгрупп; системы показателей; видов таблиц.

Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности группировка – это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам.

Устойчивое разграничение объектов выражается классификацией, которая основывается на самых существенных признаках (например, классификация отраслей народного хозяйства, классификация основных фондов и т.д.). Таким образом, классификация – это узаконенная, общепринятая, нормативная группировка.

Метод группировки основывается на следующих категориях – это группировочный признак, интервал группировки и число групп.

Группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы.

Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Интервалы бывают:

равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова;

неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе;

открытые, когда имеется только либо верхняя, либо нижняя граница;

закрытые, когда имеются и нижняя, и верхняя границы.

5. Абсолютные и относительные статистические величины.

Абсолютная величина — объем или размер изучаемого события или явления, процесса, выраженного в соответствующих единицах измерения в конкретных условиях места и времени.

Виды абсолютных величин:

• Индивидуальная абсолютная величина — характеризует единицу совокупности

• Суммарная абсолютная величина — характеризует группу единиц или всю совокупность

Результатом статистического наблюдения являются показатели, которые характеризуют абсолютные размеры или свойства изучаемого явления у каждой единицы наблюдения. Они называются индивидуальными абсолютными показателями. Если показатели характеризуют всю совокупность в целом, они называются обобщающими абсолютными показателями. Статистические показатели в форме абсолютных величин всегда имеют единицы измерения: натуральные или стоимостные.

Формы учета абсолютных величин:

• Натуральный — физические единицы (штук, человек)

• Условно-натуральный — применяется при подсчете итогов по продукции одинакового потребительского качества но широкого ассортимента. Перевод в условное измерение осуществляется с помощью коэффициента пересчета: К_{пересчета}=фактическое потребительское качество / эталон (заранее заданное качество)

• Стоимостной учет — денежные единицы

Натуральные единицы измерения бывают простыми, составными и условными.

Простые натуральные единицы измерения — это тонны, километры, штуки, литры, мили, дюймы и т. д. В простых натуральных единицах также измеряется объем статистической совокупности, т. е. число составляющих ее единиц, или объем отдельной ее части.

Составные натуральные единицы измерения имеют расчетные показатели, получаемые как произведение двух или нескольких показателей, имеющих простые единицы измерения. Например, учет затрат труда на предприятиях выражается в отработанных человеко-днях (число работников предприятия умножается на количество отработанных за период дней) или человеко-часах (число работников предприятия умножается на среднюю продолжительность одного рабочего дня и на количество рабочих дней в периоде); грузооборот транспорта выражается в тонно-километрах (масса перевезенного груза умножается на расстояние перевозки) и т. д.

Условно-натуральные единицы измерения широко используют в анализе производственной деятельности, когда требуется найти итоговое значение однотипных показателей, которые напрямую несопоставимы, но характеризуют одни и те же свойства объекта.

Натуральные единицы пересчитываются в условно-натуральные путем выражения разновидностей явления в единицах какого-либо эталона.

Например:

• различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 МДж/ кг

• мыло разных сортов — в условное мыло с 40%-ным содержанием жирных кислот

• консервы различного объема — в условные консервные банки объемом 353,4 см3,

• для подсчета общего объема работы транспорта складывают тонно-километры перевезенных грузов и пассажиро-километры, произведенные пассажирским транспортом, условно приравнивая при этом перевозку одного пассажира к перевозке одной тонны груза и т. д.

Перевод в условные единицы осуществляется с помощью специальных коэффициентов. Например, если имеется 200 т мыла с содержанием жирных кислот 40% и 100 т с содержанием жирных кислот 60%, то в пересчете на 40%-ное, получим общий объем 350 т условного мыла (коэффициент пересчета определяется как отношение 60 : 40 = 1,5 и, следовательно, 100 т · 1,5 = 150 т условного мыла).

Относительные статистические величины — это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин.

Основное условие правильного расчета относительных величин — сопоставимость сравниваемых величин и наличие реальных связей между изучаемыми явлениями.

Относительная величина = сравниваемая величина / базис

• Величина, находящаяся в числителе соотношения, называется текущей или сравниваемой.

• Величина, находящаяся в знаменателе соотношения, называется основанием или базой сравнения.

По способу получения относительные величины — это всегда всегда величины производные (вторичные).

Они могут быть выражены:

• в коэффициентах, если база сравнения принимается за единицу (АбсВеличина / Базис) * 1

• в процентах, если база сравнения принимается за 100 (АбсВеличина / Базис) * 100

• в промилле, если база сравнения принимается за 1000 (АбсВеличина / Базис) * 1000 Например показатель рождаемости в форме относительной величины, исчисляемый в промилле показывает число родившихся за год в расчете на 1000 человек.

• в продецимилле, если база сравнения принимается за 10000 (АбсВеличина / Базис) * 10000

Различают следующие виды относительных статистических величин:

• Относительная величина динамики

• Относительная величина планового задания

• Относительная величина выполнения плана

• Относительная величина структуры

• Относительная величина координации

• Относительная величина интенсивности

• Относительная величина сравнения

Относительная величина координации

Относительная величина координации (показатель координации) — представляет собой соотношение частей совокупности между собой. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо иной точки зрения.

ОВК = показатель характеризующий часть совокупности / показатель характеризующий часть совокупности, выбранную за базис сравнения

Относительная величина координации показывает, во сколько раз одна часть совокупности больше или меньше другой, принятой за базу сравнения, или сколько процентов от нее составляет, или сколько единиц одной части целого приходится на 1, 10, 100, 1000,..., единиц другой (базисной) части. Например в 1999 г. в России насчитывалось 68,6 млн.мужчин и 77,7 млн.женщин, следовательно, на 1000 мужчин приходилось (77,7/68,6)*1000=1133 женщины. Аналогично можно рассчитать сколько на 10 (100) инженеров приходится техников; число мальчиков, приходящихся на 100 девочек среди новорожденных и др.

Относительная величина структуры (показатель структуры)- характеризует удельный вес части совокупности в ее общем объеме. Относительную величину структуры часто называют "удельный вес" или "доля".

ОВС = показатель, характеризующий часть совокупности / показатель по всей совокупности в целом

Относительная величина сравнения (показатель сравнения) — характеризует соотношение между разными совокупностями по одноименным показателям.

6. Средние величины и показатели вариации.

Средняя величина - это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.

Существует 2 класса средних величин: степенные и структурные.

К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средниеразличных видов.

Степенные средние величины

Степенные средние могут быть простыми и взвешенными.

Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:

Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

где X – значения отдельных статистических величин или середин группировочных интервалов;

Средняя арифметическая

Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).

Средняя арифметическая взвешенная имеет следующий вид:

где f - количество величин с одинаковым значением X (частота).

Средняя гармоническая

Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

Средняя геометрическая

Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.

Средняя квадратическая

Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.

Средняя кубическая

Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.

Статистическая мода

Статистическая мода - это наиболее часто повторяющееся значение величины X в статистической совокупности.

Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) илимультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.

Например, на предприятии работает 16 человек: 4 из них - со стажем 1 год, 3 человека - со стажем 2 года, 5 - со стажем 3 года и 4 человека - со стажем 4 года. Таким образом, модальный стаж Мо=3 года, поскольку частота этого значения максимальна (f=5).

Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:

где Мо – мода; Х_НМо – нижняя граница модального интервала; h_Мо – размах модального интервала (разность между его верхней и нижней границей); f_Мо – частота модальноого интервала; f_Мо-1 – частота интервала, предшествующего модальному; f_Мо+1 – частота интервала, следующего за модальным.

Например, на предприятии 10 работников со стажем работы до 3 лет, 20 - со стажем от 3 до 5 лет, 5 работников - со стажем более 5 лет. Рассчитаем модальный стаж работы в модальном интервале от 3 до 5 лет: Мо = 3 + 2*(20-10)/(2*20-10-5) = 3,8 (года).

Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.