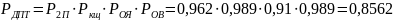3 Разработка структурных схем элементов электромеханической системы
Вероятность безотказной работы системы автоматизированного управления (САУ) в курсовой работе по заданию считаем, t=1500 часов.
3.1 Контакторы КМ1, КМ2
Структурная схема для расчета надежности КМ1 (или КМ2) примет вид:
Рисунок 3.1 – Структурная схема КМ1 (или КМ2)
3.1.1 Вероятность безотказной работы одного контактора рассчитывают по формуле:
или
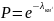
где
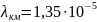[Л1] – интенсивность отказов одного
контактора, [1/ч].
Вероятность безотказной работы 1 контактора (КМ1 или КМ2) для времени t = 1000часов:
3.1.2 Вероятность безотказной работы контакторов КМ1 и КМ2 работающих на включение и отключение цепи:
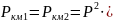
Вероятность безотказной совместной работы контакторов КМ1, КМ2:
3.2 контакторы КМ3- КМ6
Вероятность безотказной работы КМ3 – КМ6
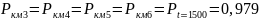
Вероятность безотказной работы группы контакторов КМ3 – КМ6
3.3 Реле времени
Используем пневматическое реле времени РПВ-110.
Интенсивность
отказов реле
Вероятность безотказной работы рассчитывается по экспонентному закону:
При наличии 4 реле времени вероятность безотказности всех реле составляют:
3.4 Силовой резистор (3 секции, проволочный, мощный)
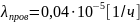
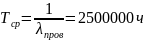
3.5 Тормозной резистор
3.6 Двигатель постоянного тока
Слабые элементы по надежности:
- подшипниковый узел(ПУ);
- коллекторно-щеточный узел(КЩУ);
- обмотка якоря(ОЯ);
- обмотка возбуждения(ОВ).
Структурная схема расчета надежности ДПТ:
ПУ
КЩУ
ОЯ
ОВ
Рисунок 3.2 - Структурная схема надежности ДПТ
3.6.1 Подшипниковый узел
Вероятность безотказной работы определяется с помощью распределения Вейбулла:
где
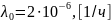– параметр определяющий масштаб;
к = 1,25 – параметр асимметрии распределения.
тогда
для t
=
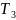= 1500 часов
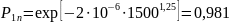
для двух узлов
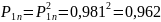
3.6.2 Коллекторно-щеточный узел
Вероятность
безотказной работы узла для времени
t=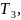
определяется с помощью центрированной
функции Лапласа:
где
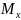= 5000 ч – математическое ожидание
безотказной работы;
=
1500ч – среднеквадратичное отклонение
ожидания;
F – функция [сборник задач Кузнецова, таблица 1].
Определяем аргумент:
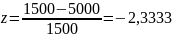
По
таблице находим функцию
тогда:
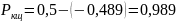
3.6.3 Обмотка якоря(ОЯ) двигателя
Вероятность безотказной работы ОЯ вычисляется с помощью центрированной и нормированной логарифмической функции Лапласа:
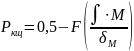
где M – логарифм математического ожидания;
-
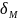логарифм среднеквадратичного отклонения.
Пример в расчете:
М = 8,7; = 1,03
Тогда получим:
=
0,5 – F(-1,3597)
=
= 0,5 – (-0,4131) = 0,91
3.6.4 Обмотка возбуждения (ОВ) двигателя
Вероятность безотказной работы ОВ рассчитывается в соответствии с экспоненциальным законом распределения:
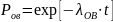
Примем:
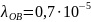1/ч
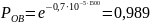
Результирующая вероятность безотказной работы ДПТ при
t=
