3.3 Оценка точности системы

Для оценки статической и вынужденной ошибок системы необходимо определить передаточную функцию замкнутой системы по ошибке:

Ф_х(р) = 1- Ф(р) =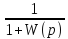 = (11.0)

Для уравнения (11.0) в общем виде :

Ф_х(р) =,

где = 0;

= 1;

=T₁+T₂= 2.064;

=T₁·T₂= 0.128;

=k= 0.44;

= 1;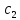=T₁+T₂= 2.064;

=T₁·T₂= 0.128.

Представим Ф_х(р) в виде бесконечного степенного ряда:

Ф_х(р) =S₀+S₁·p+S₂·p²+…,

где коэффициенты ошибок S_nопределяются по формуле:

S_n = (-).

Определим коэффициенты ошибок:

S₀== 2.2;S₁=(-S₀·) = (1- 2.2*1) = 1.07;

S₂ =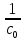(- (S₁·+S₀·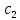)) = (1.07- (1.07·1+2.2*2.064)) = 0.0298;

Находим выражение вынужденной ошибки системы:

∆_x(t) = S₀·x_вх(t) + S₁ + S₂ .

где S₀-коэффициент статической ошибки,

S₁-коэффициент скоростной ошибки,

S₂-коэффициент ошибки от ускорения,

x_вх(t)-заданное значение выходного параметра системы.

∆_x(t) = 0.01 + 0.0298 ,

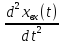при x_вх(t) = 1x(t) = 0 – статическая ошибка системы отсутствует (т.к. система астатическая);

при x_вх(t) =tx(t) = 0.01 – скоростная ошибка постоянна;

при x_вх(t) =t²x(t) = 0.01t+ 0.0298 – ошибка от ускорения линейно возрастает с течением времени.

Заключение

В данной курсовой работе была исследована система пластинчатого электрофильтра. Сначала, система была исследована на устойчивость с помощью алгебраического и частотного критериев: запас устойчивости по фазе составил 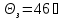запас устойчивости по амплитуде

В обоих случаях система оказалась устойчивой. Помимо этого была построена область устойчивости в плоскости параметров k_р и Т_оу. Точка М_контрпопала в эту область. Затем построили график переходного процесса в системе путем численного решения дифференциального уравнения с помощью программыMathCAD13. По графику видно, что процесс апериодический, перерегулирование равно 15%. В результате получили длительность переходного процесса системыt_пп=11.5 с.

Библиографический список

1. Бесекерский, А.В. Теория систем автоматического управления / А.В Бесекерский, Е.П. Попов – СПб.: Профессия, 2004. – 752 с.

2. Веревкин С.И. Газгольдеры – Москва:1966. 293с.

3. Касаткин А.Г. Основные процессы и аппараты химической технологии: Учебник для вузов. – 11-е изд., стереотипное, доработанное. Перепеч. с изд. 1973 г. – М.: ООО ТИД «Альянс», 2005. – 753 с.

4. Федотов А.В. Анализ и синтез автоматического регулирования при проектировании средств автоматизации: Учебное пособие. – Омск: Изд-во ОмГТУ, 1995. – 48 с.

5. Федотов А.В. Теория автоматического управления: Конспект лекций.-Омск: Издательство ОмГТУ, 2007. 176 с.

6. Описание источника питания Б5-71/1 [Электронный ресурс]- режим доступа

http://www.dc-istochnik.ru

7. Паспортные данные источника питания Б5-71/1 [Электронный ресурс]- режим доступа

http://www.dc-istochnik.ru/laboratornye-reguliruemye-istochniki-pitaniya-postoyannogo-toka-impulsnye-stabilizirovannye-B5-71-1-B5-71-2-B5-71-4

38