3. Анализ качества системы регулирования.

3.1 Оценка качества системы по логарифмическим характеристикам.

1. Оценку быстродействия в системе производим по частоте среза. Для системы удовлетворительного качества в первом приближении длительность t_пппереходного процесса связана с частотой среза следующей зависимостью[5]:

(9.0)

В нашем случае: ω_с=0.5. Тогда быстродействие системы будет изменяться в следующих пределах:

6.28<t_п<25,12 (9.1)

2) Исходя из ЛАХ системы с настроенными параметрами, запас устойчивости системы по амплитуде L₂, который определяется как

= ∞, (9.2)

где _ - частота, соответствующая углу фазового сдвига –, в нашем случае равен бесконечности, так как график ЛФХ не пересекает ось частот. Это означает, что в системе отсутствует перерегулирование.

3) Запас устойчивости системы по фазе определим как

(9.3)

где _с3 - частота среза системы,

(_с3)- фазовый угол системы на частоте среза.

Подставляя найденные по графику (см. рис. 7) значения в (9.3)получаем

что удовлетворяет условию: , т.е. склонность к потере устойчивости у системы невелика.

3.2 Исследование качества системы методом оценки переходного процесса.

Определим уравнение переходного процесса. Передаточная функция замкнутой системы (7.0) имеет вид:

тогда дифференциальное уравнение системы в операторной форме будет иметь вид

Для того чтобы решение стало возможным, структуру системы необходимо преобразовать к виду, показанному на рис. 11.

Рис. 11. Структура системы

Получим систему уравнений:

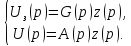(10.0)

(10.1)

Для построения графика переходного процесса дифференциальное уравнение решим численным методом, в результате чего получим таблицу решений, дающую точки графика. При численном решении дифференциального уравнения методом Рунге-Кутты третьего порядка следует преобразовать в систему уравнений первого порядка. Для этого выполняется подстановка вида

В результате этих подстановок и с учетом связей между новыми переменными получим систему дифференциальных уравнений первого порядка:

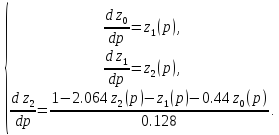(10.2)

Общее решение уравнений системы в целом определим по формуле:

,

Решим дифференциальное уравнение и построим график переходного процесса при помощи MathCAD 13. Для этого зададим шаг решения равный 200, предел измерения текущего времени равного 12.56, начальные условия равны нулю.

Для этого в MathCADвведём следующие уравнения:

(10.3)

• Функция для правых частей:

(10.4)

• Решение дифференциального уравнения методом Рунге-Кутта:

(10.5)

• Конечный результат для вычисления переходного процесса:

(10.6)

Найденные значения представлены в таблицах 8 и 9.

Таблица 8 Расчет точек переходного процесса

Таблица 9 Расчет точек переходного процесса

График переходного процесса изображен на рисунке 12.

Рис.8График переходного процесса системы

По графику переходного процесса можно определить, что в системе присутствует перерегулирование. График имеет колебательный апериодический характер.

Длительность переходного процесса, определим как время, прошедшие от начала переходного процесса (t = 0) до момента установления сигнала, отличающегося не более чем на 5% от установившегося значения. По графику переходного процесса (рис. 12) определим:

t_пп=11.5 с.

Полученное значение оказалось меньше оценочного времени переходного процесса.

Величина перерегулирования определяется из соотношения (в процентах):

σ = 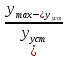· 100% =· 100% = 15 %, (10.7)

где ,- наибольшее и установившееся значения выходного параметра, определяемые по графику переходного процесса.