1.2 Структурная схема и передаточная функция системы

В соответствии со структурным методом построения математической модели системы, исходный рисунок анализа системы пластинчатого электрофильтра (рис.1) заменим упрощенной функциональной схемой (рис.4). Для этого разобьем исходную систему на функциональные элементы, каждый из которых можно будет представить типовым структурным звеном.

В качестве функциональных элементов выделим пластинчатый электрофильтр – ОУ (объект управления, представленный инерционным звеном), источник питания Б5-76/1 – ИМ (исполнительный механизм, который является безынерционным (усилительным) звеном), датчик SIEMENS SITRANS T3K PA– Д (датчик, который представлен инерционным звеном), регулятор – Р (регулятор, который определим только после построения ЛАХ и ЛФХ по исходным значениям указанным в бланке задания).

Контролируемый параметр U_у(р) – температура пластинчатого электрофильтра.

Входной сигнал системы U_з(р) – заданная температура.

Функциональная схема пластинчатого электрофильтра представлена на рис. 3.

Рис. 3. Функциональная схема пластинчатого электрофильтра.

На основе функциональной схемы и описания элементов передаточными функциями составим структурную схему исследуемой системы. Для этого в условных обозначениях звеньев запишем конкретные выражения их передаточных функций в численном виде.

Структурная схема данной системы приведена на рис. 4.

Рис.4. Структурная схема системы.

Заменяя функциональные элементы в функциональной схеме операторами этих элементов, получим структурную схему системы автоматического управления (рис. 5).

Рис.5Преобразованная структурная схема системы.

Для получения передаточной функции замкнутой системы преобразуем полученную структурную схему к замкнутой системе с единичной обратной связью. Для этого перенесем сравнивающий элемент с выхода измерительного усилителя на вход электрофильтра, при этом необходимо между переносимым задающим воздействием и сравнивающим элементом добавить фиктивное звено с передаточной функцией, обратной передаточной функции исходного звена, находившегося в обратной связи. Добавление такого звена позволяет нам сохранить сигналы в системе неизменными, так как звено не оказывает влияния на динамические свойства системы мы можем им пренебречь, то есть избавиться от него в дальнейшем. При этом будем учитывать все правила нахождения передаточной функции соединений звеньев [4]:

. (4.0)

Передаточная функция разомкнутой системы W(p) будет иметь вид:

(4.1)

где k_o=k_им*k_д*k_об=0.00013*0.340*0.022=0.000000972

После подстановки рассчитанных числовых параметров системы в W(p) получим:

(4.1)

По передаточной функции разомкнутой системы определим передаточную функцию замкнутой системы:

(4.2)

где А(р)- числитель передаточной функции разомкнутой системы,

В(р)- знаменатель передаточной функции разомкнутой системы,

G(р)-характеристический полином замкнутой системы,

отсюда

(4.3)

2. Расчет настроек регулятора.

2.1 Построение логарифмических характеристик без учёта настроек регулятора.

Построим ЛАХ без учета регулятора, то есть примем Тогда передаточная функция разомкнутой системы будет иметь следующий вид:

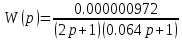, (5.0.)

Определим значение логарифмического коэффициента усиления L() для единичной частоты:

, (5.1.)

где К – коэффициент усиления системы;

Подставляя известные значения в (5.1.), получаем:

(5.2)

Исходя из (5.0.) мы имеем две частоты сопряжения, вычислим их по формуле:

(5.3)

где Т - постоянная времени звена входящего в выражение передаточной функции.

Подставляя известные значения в(5.3), получаем

(5.4)

(5.5)

Для датчика и трубчатого электрофильтра соответственно.

Запишем выражение для фазовой характеристики:

(5.6)

Где ,- фазовые сдвиги, соответствующие инерционным звеньям: датчикуSIEMENSSITRANST3KPAи пластинчатому электрофильтру.

Значения фазового угла ₁() для ряда частот приведены в таблице 5.

ω, рад/с	φi(ω), град
0	0
0.1	-11.65
0.2	-22.48
0.3	-31.9
0.5	-46.71
1	-66.86
2	-82.8
3	-90.74
10	-118.1
16	-132.04
30	-150
100	-170.24

Таблица 5. Изменение значение фазового угла для ряда частот.

График логарифмической амплитудно-частотной характеристики представляет собой три участка:

• Низкочастотный интервал (₁). Так как для объекта управления не учитываем астатичность, прямая линия с наклоном 0 дБ/дек по отношению к оси частот будет проходить через точку (₁; L₁(1)).

• Среднечастотный интервал (₁<₂). При частоте первой частоте сопряжения ₁ начинает влиять инерционность объекта на систему, поэтому наклон прямой по отношению к оси частот будет равен -20 дБ/дек.

• Высокочастотный интервал (>₂). На этом участке на систему начнет влиять инерционность исполнительного механизма, поэтому прямая будет иметь наклон по отношению к оси частот -40 дБ/дек.

Построенные логарифмическая амплитудно-частотная характеристика и логарифмическая фазовая характеристика системы без учета влияния регулятора изображены на чертеже КР-2068.998-26-04-00.00.000.Д стр. 15 кривыми L₁(ω) и φ₁(ω). Из построения видно, что система является неустойчивой.