
4.Расчетная часть
Рассмотрим конкретный пример:

Математическая форма записи задачи выглядит следующим образом:
![]()
![]()
![]()
![]()
Запишем задачу в канонической форме
![]()
![]()
![]()
![]()
Для выделения допустимого базиса воспользуемся методом искусственного базиса:

Подставим числа в уравнения

Запишем симплекс таблицу:
|
|
B |
|
|
|
|
|
|
|
|
17 |
-7 |
-6 |
1 |
-1 |
-1 |
-1 |
|
|
3 |
0 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
|
6 |
0 |
0 |
0 |
0 |
0 |
-1 |
|
|
21 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
119 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
1120 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
3 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
-3 |
1 |
0 |
0 |
-1 |
0 |
|
|
6 |
-5 |
-7 |
1 |
0 |
0 |
-1 |
|
|
B |
|
|
|
|
|
|
|
|
11 |
-2 |
1 |
-1 |
-1 |
-1 |
0 |
|
|
3 |
0 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
|
6 |
0 |
0 |
0 |
0 |
0 |
-1 |
|
|
21 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
119 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
1114 |
5 |
7 |
-1 |
0 |
0 |
1 |
|
|
3 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
-3 |
1 |
0 |
0 |
-1 |
0 |
|
|
6 |
-5 |
-7 |
1 |
0 |
0 |
-1 |
|
|
B |
|
|
|
|
|
|
|
|
3 |
1 |
-1 |
-1 |
-1 |
0 |
0 |
|
|
3 |
0 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
|
6 |
0 |
0 |
0 |
0 |
0 |
-1 |
|
|
21 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
111 |
3 |
-1 |
0 |
0 |
1 |
0 |
|
|
1058 |
26 |
-7 |
-1 |
0 |
7 |
1 |
|
|
3 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
-3 |
1 |
0 |
0 |
-1 |
0 |
|
|
62 |
-26 |
7 |
1 |
0 |
-7 |
-1 |
|
|
B |
|
|
|
|
|
|
|
|
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
|
|
3 |
0 |
0 |
0 |
-1 |
0 |
0 |
|
|
8 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
|
6 |
0 |
0 |
0 |
0 |
0 |
-1 |
|
|
18 |
-1 |
0 |
0 |
1 |
0 |
0 |
|
|
102 |
-3 |
-1 |
0 |
3 |
1 |
0 |
|
|
980 |
-26 |
-7 |
-1 |
26 |
7 |
1 |
|
|
3 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
|
17 |
3 |
1 |
0 |
-3 |
-1 |
0 |
|
|
140 |
26 |
7 |
1 |
-26 |
-7 |
-1 |
Симплекс таблица оптимальная, все дополнительные переменные не базисные и = 0, значит можно записать симплекс-таблицу для данной задачи.
|
|
B |
|
|
|
|
|
-31 |
3 |
2 |
1 |
|
|
3 |
-1 |
0 |
0 |
|
|
8 |
0 |
-1 |
0 |
|
|
6 |
0 |
0 |
-1 |
|
|
18 |
1 |
0 |
0 |
|
|
102 |
3 |
1 |
0 |
|
|
980 |
26 |
7 |
1 |
|
|
3 |
-1 |
0 |
0 |
|
|
17 |
-3 |
-1 |
0 |
|
|
140 |
-26 |
-7 |
-1 |
|
|
B |
|
|
|
|
|
-85 |
-3 |
2 |
1 |
|
|
21 |
1 |
0 |
0 |
|
|
8 |
0 |
-1 |
0 |
|
|
6 |
0 |
0 |
-1 |
|
|
18 |
1 |
0 |
0 |
|
|
48 |
-3 |
1 |
0 |
|
|
512 |
-26 |
7 |
1 |
|
|
21 |
1 |
0 |
0 |
|
|
71 |
3 |
-1 |
0 |
|
|
608 |
26 |
-7 |
-1 |
|
|
B |
|
|
|
|
|
-181 |
3 |
-2 |
1 |
|
|
21 |
1 |
0 |
0 |
|
|
56 |
-3 |
1 |
0 |
|
|
6 |
0 |
0 |
-1 |
|
|
18 |
1 |
0 |
0 |
|
|
48 |
-3 |
1 |
0 |
|
|
176 |
-5 |
-7 |
1 |
|
|
21 |
1 |
0 |
0 |
|
|
119 |
0 |
1 |
0 |
|
|
944 |
5 |
7 |
-1 |
|
|
B |
|
|
|
|
|
-235 |
-3 |
-2 |
1 |
|
|
3 |
-1 |
0 |
0 |
|
|
110 |
3 |
1 |
0 |
|
|
6 |
0 |
0 |
-1 |
|
|
18 |
1 |
0 |
0 |
|
|
102 |
3 |
1 |
0 |
|
|
266 |
5 |
-7 |
1 |
|
|
3 |
-1 |
0 |
0 |
|
|
119 |
0 |
1 |
0 |
|
|
854 |
-5 |
7 |
-1 |
|
|
B |
|
|
|
|
|
-501 |
-8 |
5 |
-1 |
|
|
3 |
-1 |
0 |
0 |
|
|
110 |
3 |
1 |
0 |
|
|
272 |
5 |
-7 |
1 |
|
|
18 |
1 |
0 |
0 |
|
|
102 |
3 |
1 |
0 |
|
|
281 |
5 |
-7 |
1 |
|
|
3 |
-1 |
0 |
0 |
|
|
119 |
0 |
1 |
0 |
|
|
1120 |
0 |
0 |
1 |
|
|
B |
|
|
|
|
|
-1011 |
-23 |
-5 |
-1 |
|
|
3 |
-1 |
0 |
0 |
|
|
8 |
0 |
-1 |
0 |
|
|
986 |
26 |
7 |
1 |
|
|
18 |
1 |
0 |
0 |
|
|
102 |
3 |
1 |
0 |
|
|
995 |
26 |
7 |
1 |
|
|
3 |
-1 |
0 |
0 |
|
|
17 |
-3 |
-1 |
0 |
|
|
1120 |
0 |
0 |
1 |
Оптимальное
решение.
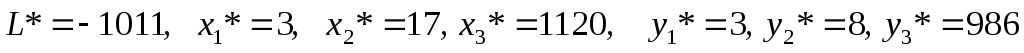
Отсюда
следует, что максимальная стоимость произведенного конечного продукта равна 1011 рублей, объем производства первого продукта равен 3, второго – 17, третьего – 1120 и план выпуска конечной продукции 3, 8, 986.
