
Nerovnice
Nerovnice s jednou neznámou:
Lineární nerovnice: lineární nerovnice s neznámou ve jmenovateli, s parametrem, s absolutními hodnotami
Kvadratické nerovnice: kvadratické nerovnice s neznámou ve jmenovateli, s parametrem, s absolutními hodnotami
Iracionální nerovnice
Algebraické nerovnice vyššího stupně v rozloženém tvaru
Algebraické nerovnice řešené metodou substituce
Nerovnice se dvěma s více neznámými
Soustavy nerovnic s dvěma a více neznámými
Nerovnice s jednou neznámou
Nerovnice o jedné neznámé je zápis nerovnosti dvou výrazů ve tvaru:
L(x) > P (x), L(x) < P (x), L(x)
 P
(x), L(x)
P
(x), L(x)
 P (x), s proměnou x
a z daného číselného oboru M.
P (x), s proměnou x
a z daného číselného oboru M.
Terminologie je stejná jako u rovnic.
Řešením nerovnice nazýváme každé číslo, jeho dosazením do nerovnice za neznámou dostaneme pravdivou nerovnost. Všechna řešení dané nerovnice zapisujeme do množiny kořenů K.
Dvě nerovnice, které mají stejné množiny řešení, nazýváme ekvivalentní nerovnice.
Nerovnice řešíme stejnými postupy jako rovnice a shrnujeme závěr řešení.
Vzhledem k tomu, že M
 R,
je také často K
R,
tedy množina nekonečně mnoha reálných čísel.
R,
je také často K
R,
tedy množina nekonečně mnoha reálných čísel.

3x – 7 5x – 13
13 – 7 5x – 3x
6 2x
x 3
K = <3; +
 )
)Pak je nemožné provést pro všechna tato čísla zkoušku. Proto se při řešení nerovnic snažíme používat pouze ekvivalentní úpravy.
Ekvivalentní úpravy nerovnic
Ekvivalentní úpravy nerovnice pro M R:
Výměna stran nerovnice se současnou změnou znaku nerovnice v obrácený
Nahrazení strany nerovnice výrazem, který se jí rovná v oboru řešení nerovnice (znak nerovnosti se nemění)

x + 4 > - 2x + 10
x + 2x > 10 – 4
3x > 6 │ : 3
x > 2 → x
 (+2;
)
(+2;
)– x + 4 > 2x + 10
– x – 2x > 10 – 4
– 3x > 6 │: (– 3)
→ otočíme znaménko nerovnosti
x < - 2 → x (- ; -2)
Přičtení stejného čísla nebo výrazu, který se jí rovná v oboru řešení nerovnice (znak nerovnosti se nemění)

– x
+ 4 >
 │∙
2 →vynásobíme
dvěma
│∙
2 →vynásobíme
dvěma
– 2x – 2x > 10 – 8
– 4x > 2 │ : (-4)
x < - 0,5 →otočili jsme znaménko nerovnosti
x
(- - 0,5)
- 0,5)
Vynásobení obou stran nerovnice kladným číslem nebo výrazem nabývajícím jen kladných hodnot v oboru řešení nerovnice (znak nerovnosti se nemění).
Vynásobení obou stran nerovnice záporným číslem nebo výrazem nabývajícím jen záporných hodnot v oboru řešení nerovnice se současnou změnou znaku nerovnosti v obrácený.

 │2
│2
2x2 + 4 4x2 │– 4x2
– 2x2 + 4 0 │: (-2)
Umocněním obou stran nerovnice přirozeným mocnitelem, pokud obě strany nerovnice nabývají nezáporných hodnot v oboru řešení nerovnice (znak nerovnosti se nemění)
Odmocnění obou stran nerovnice přirozeným odmocnitelem, pokud obě strany nerovnice nabývají jen nezáporných hodnot v oboru řešení nerovnice (znak nerovnosti se nemění)
Zlogaritmováním obou stran nerovnice logaritmem téhož základu, pokud obě strany nerovnice nabývají jen nezáporných hodnot v oborou řešení nerovnice, přitom změna znaku nerovnosti závisí na základu a logaritmu. Pro a > 1 se znak nerovnosti nemění, pro 0 < a < 1 se znak nerovnosti mění v obrácený.
Lineární nerovnice
Lineární nerovnice s neznámou x R je každá nerovnice ve tvaru:
ax + b > 0,
ax + b < 0,
ax + b 0,
ax + b 0, kde a, b jsou reálné koeficienty.
3
∙ (5x – 7)
12x – 20
15x – 21
12x – 20
15x – 21
12x – 20
3x
1 │:3
x
x
<1/3;
)
3 –
72
– 36x > 15 – 16x + 12 -20x
> - 45 x
<
x
<
K
3x
– 1 < 1 -
2
∙ 3x – 2 ∙ 1 < 2 ∙ 1 – 2 ∙
6x
– 2 < 2 – (2 – x) 6x
– 2 < 2 – 2 + x
5x
< 2 │:5 x
<
x




 >
>
 -
-
 │∙24
│∙24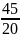


 │∙2
│∙2

Tabulka
znamének:
horní řádek
tabulky je číselná osa, kam umístíme nulové body v pořadí
podle velikosti. Do prvního sloupce tabulky umístíme pod sebe
členy součinu. Pro každý řádek zaznačíme nulou nebo
kolečkem, kde se daný výraz nuluje. Tam se bude měnit znaménko.

 ineární
nerovnice v součinovém
tvaru
ineární
nerovnice v součinovém
tvaru
Nerovnice
v součinovém tvaru
Upravíme
tak, aby na jedné straně byla 0 Členky
součinu rozložíme na co nejjednodušší výrazy Najdeme
čísla, kde se nulují členy součinu Uděláme
tabulku znamének s pomocí těchto čísel Vyberme
intervaly se správnými znaménky

x ∙ (x – 2) 0 → → → → → nulové body: 0, - 2 → → → tabulka →
Jako řešení vyberme intervaly, jejichž znaménka dopovídají požadované nerovnosti, tedy interval splňující požadovanou nervosnost je x
 .
.
Lineární nerovnice s neznámou ve jmenovateli
Převod na podílový tvar:
Při řešení nerovnic s neznámou ve jmenovateli je výhodné použít úpravu na podílový tvar nerovnice.
To znamená upravit nerovnici tak, abychom na jedné straně získali výraz ve tvaru podílu (lomený výraz, tj. zlomek), na druhé straně nerovnice 0.
V dalším řešení nerovnice už jen porovnáme lomený výraz s nulou.
Nerovnice v podílovém tvaru: Jsou nerovnice, které obsahují na jedné straně podíl a libovolného počtu lineárních členů nebo dvojčlenů.
Např.:
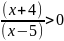
 1
1  0
0  - 2
- 2
< 1 │
- 1
– 1 < 0
 < 1
< 1  < 0 K
= ( - 2/3;
)
< 0 K
= ( - 2/3;
)
→Pro
splnění této nerovnice
musí platit: 2x
+ 3 > 0, tedy x > -

Násobení jmenovatelem:
Pokud bychom chtěli násobit výrazem s neznámou, musíme násobení rozdělit do dvou podmínek.
Buď výraz nabývá kladných hodnot
Nebo výraz nabývá záporných hodnot v oboru řešení nerovnice.

Postup:
Nerovnici převedeme na podílový tvar
Čitatele i jmenovatele porovnáváme s nulou s příslušným znaménkem nerovnosti
Podle dané podmínky se pak násobením nerovnice nemění nebo mění znaménko nerovnosti.
Násobení
výrazem (2x + 3):
< 1
< 1 │
∙ (2x + 3)
Jestliže
2x + 3 > 0, tzn. x > - 2/3, pak to po vynásobením nerovnice
přejdeme en ekvivalentní nerovnici 2x < 2x + 3, které vyhovují
všechna reálná čísla, ale vzhledem k podmínce je K1
= (-2/3,
).
Jestliže
2x + 3 tzn. x < - 2/3, pak to vynásobení nerovnice přejdeme na
ekvivalentní nerovnici 2x > 2x + 3, která nemá řešení.
Proto K2
= { }. Výsledná
množina kořenů zadané nerovnice je: K =
K1

 K2 =
K2 =

Kvadratické nerovnice
Kvadratické nerovnice s neznámou x R je každá nerovnice tvaru:
ax2 + bx + c < 0
ax2 + bx + c > 0
ax2 + bx + c 0
ax2 + bx + c 0
Při řešení kvadratické nerovnice prostupujeme tak, že nejprve najdeme kořeny odpovídající kvadratické rovnici x1 a x2. Pokud tyto kořeny existují, rozložíme kvadratický trojčlen na součin a dál řešíme nerovnici v součinném tvaru, tedy součin dvou lineárních dvojčlenů porovnáváme s nulou.
x2 – 2x – 3 > 0
(x – 3) ∙ (x + 1) > 0
Příklad: x2 – 2x – 3 > 0
Výsledek
zapisujeme K = K1
K2
= (-
 (3,
)
(3,
)
K = {-1, 3}
K1
= (3,
) K2
= (-

Rozklad na součin:
(x – 3) ∙ (x + 1) > 0
Regresivní a korelační analýza
Regresivní analýzou zkoumáme průběh a korelační analýzou zkoumáme těsnost závislostí mezi kvantitativními znaky – vztahy závislé proměnných (y) na nezávisle proměnných (x)
Předpoklad: Před každým výpočtem, je nezbytně nutné se ujistit, že mezi proměnnými závislost existuje!
Regresní analýza
Regrese je vyjádřena matematickou funkcí, která udává vlastní průměrný průběh sledované závislosti mezi proměnnými x a y. Parametry regresivní funkce jsou počítány.
Před vlastním výpočtem regresní funkce je nutno zvolit vhodný typ funkce pro vyjádření průměrného průběhu závislostí.
Typy regresivních funkcí:
Lineární funkce y = a + bx
Kvadratické funkce y = a + b1 x + b2 x2
Odmocninná funkce y = a + b1 x + b2
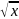
Logaritmická funkce y = a + b logx
Mocninná funkce y = axb
Exponenciální funkce y = abx
Pomocí regresivních funkcí se hodnotám nezávisle proměnné x přiřazují průměrné (střední) hodnoty závisle proměnné y.
Lineární funkce
Lineární funkce y = a + bx je rovnici přímky.
a…absolutní člen
b… regresní koeficient
x … nezávsle proměnná
y … závislé proměnná
Je-li regresní funkcí přímka, jedná se o lineární regresi.
Lineární regrese
Vynesení skutečně zjištěných uspořádaných dvojic proměnných
 do pravoúhlého osového systému – bodový diagram.
do pravoúhlého osového systému – bodový diagram.
Korelační pole
Vyneseno uspořádané dvojice odpovídajících údajů vytvářející korelační pole.
Korelačním polem probíhá vhodně zvolená regresivní funkce. Vhodně zvolená regresní funkce – regresní přímka dobře kopíruje korelační pole.
Korelační pole vhodně nekopíruje nelineární funkce.
