Аддитивная модель данных двухфакторного эксперимента при независимом действии факторов

Для описания данных таблицы 7.1 двухфакторного эксперимента в большинстве случаев оказывается приемлемой аддитивная модель. Она предполагает, что значение отклика хц является суммой самостоятель­ных вкладов соответствующих уровней каждого из факторов и незави­симых от этих факторов случайных величин. Последние отражают вну­треннюю изменчивость отклика при фиксированных уровнях факторов, которая может порождаться различными причинами.

Таким образом, каждое наблюдение хц представляется в виде:

При этом числа b\,... ,b_n являются результатом влияния на отклик мешающего фактора В, действие которого разбивает все данные на бло­ки. Поэтому величины Ь_х,... , Ь_п называют эффектами блоков. Числа t%,... , tk отражают действие на отклик интересующего нас фактора А и именуются эффектами обработки. Относительно случайных величин

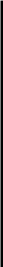eij предполагается, что они одинаково распределены и независимы в совокупности. Различные методы двухфакторного анализа требуют от их распределения либо только непрерывности, либо принадлежности к нормальному семейству распределений N(0,a²) со средним 0 и некото­рой неизвестной дисперсией а². Оба эти случая разобраны ниже.

Непараметрические критерии проверки гипотезы об отсутствии эффектов обработки

Критерий Фридмана (произвольные альтернативы)

Непараметрический критерий Фридмана для проверки гипотезы Н_о против альтернативы о наличии влияния фактора А используется в случае, если о распределении случайных величин ец, г = 1,... , п, j = 1,... , fc в модели (7.2) известно только то, что оно непрерывно, а сами величины eij независимы в совокупности. (То, что е^- одинаково распределены, было оговорено раньше.) Критерий основан на идее пе­рехода от значений величин хц в таблице двухфакторного анализа к их рангам. В отличие от однофакторного анализа, ранжирование происхо­дит не по всей совокупности величин хц, а поблочно, то есть рассма­тривается каждая отдельная строка таблицы 7.1 и при фиксированном индексе i осуществляется ранжирование величин Жу при j = 1,... , к. Тем самым устраняется влияние «мешающего» фактора В, значение которого для каждой строки таблицы постоянно.

Обозначим полученные ранги величин хц через гц. Ясно, что значе­ния nj изменяются от 1 до fc, а соответствующая строка рангов предста­вляет собой некоторую перестановку чисел 1,2,... , fc. Для простоты из­ложения будем предполагать, что среди элементов хц, стоящих в одной строке таблицы (7.1), нет совпадающих (в противном случае следует использовать средние ранги). При гипотезе Hq : т-\_ = т₂ = • • • = Tk = О каждая строка рангов Гц, rj2,..., r,fc будет представлять случайную пе­рестановку чисел от 1 до fc, причем все fc! перестановок равновероятны. Введем величину: r.j — ^(X^=i^r«j)' являющуюся средним значением рангов по столбцу j. При гипотезе Н_о в силу равновероятности всех перестановок рангов в каждой строке значение r.j для каждого j не должно сильно отличаться от величины г.. = (fc +1)/2, которая предста­вляет собой общий средний ранг всех элементов таблицы рангов. (Дей­ствительно, сумма рангов по всей таблице есть nfc(fc -f l)/2. Средний ранг получается делением на число пк элементов таблицы).

Здесь множитель, стоящий перед знаком суммы, добавлен для того, чтобы S имело простое асимптотическое распределение. В вычислитель­ном плане более удобна другая форма записи величины S, а именно:

(7.4)

Как отмечалось выше, при справедливости гипотезы Но величины (r.j — г..)² в выражении (7.3) с большой вероятностью сравнительно малы для всех j, и, следовательно, значение S сравнительно невелико.

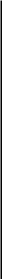А при нарушении Яо суммы рангов в одних столбцах будут тяготеть к превышению значения среднего ранга г.., а в других — к уменьшению этого значения, в зависимости от знака величины т,- ф 0. Это приводит к возрастанию статистики Фридмана S. Из этих соображений вытекает вид критерия Фридмана для проверки гипотезы Я_о : т\ = т₂ = • • • = T_fc = 0 против альтернативы наличия эффектов обработки.

Критерий Пейджа (альтернативы с упорядочением)

Назначение. Часто целью исследования является установление преимущества одного метода обработки над другим. Если таких об­работок несколько, возможно предположение, что их эффективность возрастает в определенном направлении, например, по мере увеличения интенсивности воздействия. Для того, чтобы подтвердить или опро­вергнуть такое предположение, снова обратимся к проверке Яо. Но на этот раз постараемся выбрать критерий, чувствительный именно к альтернативам о возрастании (вариант: убывании) эффекта. Против та­кой специальной и более узкой группы альтернатив можно предложить ориентированный именно на эту ситуацию критерий Пейджа.

Критерий Пейджа предназначен для проверки гипотезы Я_о об от­сутствии эффектов обработки ( До : т% = т% = • •- = ть) против аль­тернатив с упорядочением: т\ ^ Т2 ^ • • • ^ т^, где хотя бы одно из неравенств строгое.

Статистика Пейджа. Введем величину г,- как rj = Х^Г=1^гу- ⁽-'^та' тистика Пейджа L по определению есть: Вид критерия. Критерий проверки гипотезы Я_о против альтернатив с упорядочением на уровне значимости а имеет вид:

• принять Я_о, если L < l(a,k,n);

• отклонить Яо в пользу альтернативы, если L > l(a,k,n),

где функция l(a,k,n) удовлетворяет уравнению P{L > l(a,k,n)} = a.

Таблицы и асимптотика. Для значений к = 3, те = 2(1)20 и к = 4(1)8, те = 2(1)12 таблица приближенных значений l(a,k,n) дана в [115]. В случае больших значений /сите для нахождения процентных точек следует использовать асимптотическое распределение статистики L. Рассмотрим величину L*:

(7.6)

При справедливости Я_о статистика L* имеет при те —> оо асимптоти­ческое распределение N(0,1) (сведения о более точной аппроксимации можно найти в [65]). Следовательно, приближенный критерий для про­верки Я_о против альтернатив с упорядочением на уровне значимости а имеет вид: принять Я_о, если L* < z_a, в противном случае — от­клонить Я_о в пользу альтернативы. Здесь z_a — а-процентная точка стандартного нормального распределения.

Если в пределах строки исходной двухфакторной таблицы встреча­ются совпадающие значения, надо использовать средние ранги. Чем больше таких совпадений, тем более приближенными становятся вы­воды.