§ 2. Лінійна залежність

Нехай 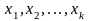вектора із лінійного простору — дійсні числа. Вектор називають лінійною комбінацією .

Очевидно, при . Але може бути, що лінійна комбінація у=0, хоча не всі коефіцієнти перетворюються в нуль. Тоді говорять, що лінійно залежні.

Визначення. Вектора називають лінійно залежними, якщо існують числа , не всі рівні нулю и такі, що

. (*)

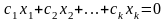Якщо рівняння (*) можливе лише при , то — лінійно незлежні. Наприклад, на площині два вектора и лінійно залежні тоді и тільки тоді, коли и колінеарні. У просторі же лінійна незалежність векторів еквівалентна їх некомпланарності.

Як було показано (юніта 1), система векторів

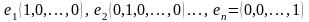
із арифметичного простору лінійно незалежна.

Розглянемо декілька прикладів лінійно незалежних систем векторів у просторі — неперервно диференційованих функцій на відрізку .

Приклад 1. Пара функцій лінійно незалежні на будь якому відрізку . Дійсно, складемо лінійну комбінацію, прирівняємо її до 0-вектору простору . Нульовим елементом цього простору являється функція, приймаюча значення нуль у всіх точках відрізку , тобто (відрізок осі ОХ).

Це рівняння повинно виконуватися для всіх x із . Нехай х=0 спочатку, потім покладемо (вважаємо, що 0 і належать ), отримуємо: , . Умови лінійної незалежності віконані.

Система же функцій в тому же просторі — лінійно залежна, так як має місце тотожність , тут .

Приклад 2. Розглянемо простір многочленів ступеня . Система функцій лінійно незалежна.

Складемо їх лінійну комбінацію, зрівняємо нуль — вектору и знайдемо коефіцієнт :

Продиференціюємо послідовно три рази останнє рівняння, враховуючи, що похідні нуль — функції рівні нулю тотожно, отримаємо

Звідси отримаємо .

Зауважимо, що взагалі система функцій лінійно незалежна у просторі многочленів ступеня , при будь якому .

Звідси слідує, що многочлен ступеня n тотожно дорівнює нулю тоді і тільки тоді, коли всі його коефіцієнти рівні нулю, а два многочлена ступеня n рівні, якщо співпадають їх коефіцієнти при однакових ступенях х.

Надалі ми познайомимося і з іншими лінійно незалежними системами в .

Лема 1. Якщо серед векторів маються лінійно залежні, то и вся система лінійно залежна.

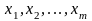
Дійсно, якщо лінійно залежна підсистема, то існує нетривіальна лінійна комбінація із цих векторів що дорівнює нуль-вектору:

(не всі рівні нулю). (*)

Тоді приписав до (*) останні вектора системи з нульовими коефіцієнтами, отримаємо

(**)

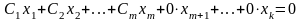і лінійна комбінація (**) також нетривіальна. Таким чином всяка підсистема лінійно незалежної системи векторів лінійно незалежна.

Лема 2. Вектора лінійно залежні тоді і тільки тоді, коли хоч би один із них є лінійна комбінація інших. Доказ очевидно відразу же із визначення лінійної залежності.

Лема 3. Якщо в систему векторів входить 0-вектор, то вона лінійно залежна, так як існує, наприклад, лінійна комбінація 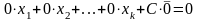, де С — будь яке, .

§ 3. Базис і координати

Поняття базису простору вже обговорювалося раніше. Аналогічно визначається базис будь якого лінійного простору.

Визначення. Кінцева система векторів називається базисом лінійного простору V, якщо:

а) вектори лінійно незалежні;

б) будь який вектор 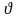простору V представляється у вигляді лінійної комбінації векторів базису:

. (*)

Коефіцієнти розкладання (*) визначаються однозначно і називаються координатами вектора в базисі . Дійсно, у іншому випадку, якщо і , де нульову лінійну комбінацію векторів , де не всі коефіцієнти рівні нулю. Це суперечить умові лінійної незалежності системи .

З єдиності розкладання слідує що два вектора рівні, якщо співпадають їх координати по будь якому базису.

Приклади.

1. В просторі трійка векторів представляють базис, а координатами будь якого вектору по цьому базису являються проекції вектора на координатні осі.

2. Стандартним базисом в просторі служить система лінійно незалежних векторів ; і кожний вектор .

3. В просторі многочленів ступеня функції утворюють базис. Лінійна незалежність цієї системи вже перевірялася. Координати будь якого многочлена по даному базису рівні . Введення базису дозволяє перейти від лінійних операцій над координатами, тобто до звичних операціях над числами.

Теорема. При додаванні векторів їх відповідні координати складаються, при множенні вектора на число всі координати його множаться на те саме число.

Перейдемо до поняття розмірності и простору.

Вивчаючи аналітичну геометрію, ми помітили, що на прямій не існує двох лінійно нерозвинених векторів; на площині будь яка пара не колінеарних векторів лінійно незалежна, але кожні три вектора вже лінійно залежні; в просторі же існує лінійно

незалежні трійки векторів (неколінеарних), але вже будь-які чотири вектори лінійно залежні.Згадані простору відрізняються своєю розмірністю * {

При вивченні простору R "(кжіта 1) ми переконалися, що в просторі можна вибрати різні базиси Всі вони володіють важливою властивістю - число їх векторів однаково.

Ця властивість справедливо для будь-якого лінійного простору Иц Визначення. Число векторів у всіх базисах простору V однаково. Це число називається розмірністю простору V і

позначати dim! '.

Якщо dim Г-л, то будь-які п лінійно незалежних векторів простору V утворюють базис. Тому пряма лінія - одномірне простір, площина - двумерна, а звичне нам простір - трехмерно.

Якщо в просторі можна вибрати будь-яке число лінійно; незалежних векторів, то його називають безконечномірним.

У просторі многочленів ступеня але вище п є базис

| З (/ * +1) вектора, тому розмірність цього простору.

дорівнює (/ 7-t)). Простір же всіх неперервних на відрізку (ajf)

функції не є конечномірні. Ми будемо розглядати простору, мають кінцеві базиси.

Приклад 1. У просторі R розглянемо два базису. Базис {#}:

XeR ~. & = (3,4) (неколінеарна) і {/}: yj = (ll). / ₂ = (0.l) J Знайдемо координати вектора х (5,8) в кожному базисі. Очевидно, вектор {

^х = ² g, + & • значить його координати в базисі {g} x _g (2,1). У той же

£

час х = 5 /, + 3 f _2, а значить x _f = (5,3).

Приклад 2. Розглянемо сукупність всіх квадратних матриць 2-го

порядку А

(Ah 4

. Як вже говорилося, вони утворюють лінійне

простір Покажемо, що його розмірність дорівнює 4. Дійсно, I

1

лінійно

система матриць про Н1 незалежна, а матриця «- лінійна

^ают "комбінація е,, * _=, с \. е,. Система матриць - базис простору.

»І | числа л Ас, </ - координати матриці І в цьому базисі. Базис складається з * 4 елементів, отже, простір чотиривимірному. Зауважимо, чт

■ простір квадратних матриць порядку г? має розмірність п.

Приклад 3. У просторі I / многочленів ступеня <2. функції

г, ^х: + 2х, ~ х - I. /, = - За год 1 утворюють базис.

Перевіримо їх лінійну незалежність.

С, д * ^2. + (2С, + С + ЗПнЗ) а + (з,-с) = о.

(С,-О

2С, + С, + ЗС ₃ = 0 •

-С, + Г ₃ = о

Звідси випливає: С, - С, = С _'3 = 0.

Ми показали, що розмірність простору 1/многочленов ступеня

<2 дорівнює 3, тому /, / _2, / ₃ - базис простору V.

*

Знайдемо координати многочлена ^/> (г) = ^5г:> 5 л: * -7 в базисі

^а А + РЛ + га = Р {*) або

# • ^ДГ: + (2 <* + Р + 3 /) Л-- / 7 квітень - у = 5х ² - 5.x * + 7.

Порівнюючи коефіцієнти при однакових степенях х в

1 _-?; А = 5

многочлене зліва і справа, отримаємо <; 2 а + р + 3 у = -5. Звідси, а = 5

Нп I -0 ^{+ УВ1}

р = -9, у = -2 координати многочлена Р (х) в базисі {/}

Согрсмеіма * Гуманігаркаа А <; Д 1 Мий

57

незалежні трійки векторів (неколінеарних), але вже будь-які чотири вектори лінійно залежні. Згадані простору відрізняються своєю розмірністю * {

При вивченні простору R "(кжіта 1) ми переконалися, що в просторі можна вибрати різні базиси Всі вони володіють важливою властивістю - число їх векторів однаково.

Ця властивість справедливо для будь-якого лінійного простору Иц Визначення. Число векторів у всіх базисах простору V однаково. Це число називається розмірністю простору V і

позначати dim! '.

Якщо dim Г-л, то будь-які п лінійно незалежних векторів простору V утворюють базис. Тому пряма лінія - одномірне простір, площина - двумерна, а звичне нам простір - трехмерно.

Якщо в просторі можна вибрати будь-яке число лінійно; незалежних векторів, то його називають безконечномірним.

У просторі многочленів ступеня але вище п є базис

| З (/ * +1) вектора, тому розмірність цього простору.

Я

дорівнює (/ 7-t)). Простір же всіх неперервних на відрізку (ajf)

функції не є конечномірні. Ми будемо розглядати простору, мають кінцеві базиси.

Приклад 1. У просторі R розглянемо два базису. Базис {#}:

XeR ~. & = (3,4) (неколінеарна) і {/}: yj = (ll). / ₂ = (0.l) J Знайдемо координати вектора х (5,8) в кожному базисі. Очевидно, вектор {

^х = ² g, + & • значить його координати в базисі {g} x _g (2,1). У той же

£

час х = 5 /, + 3 f _2, а значить x _f = (5,3).

Приклад 2. Розглянемо сукупність всіх квадратних матриць 2-го

(Ah ⁴

. Як вже говорилося, вони утворюють лінійне

(З d

простір Покажемо, що його розмірність дорівнює 4. Дійсно, I

порядку А

Важливим прикладом підпростору є лінійна оболонка векторів.

Визначення. Нехай про _Ху а _2у ... _у а _{я-система} векторів з простору V. Сукупність всіх лінійних комбінацій

а _х а _х + ал, + • • + ^а ~ ^п _т • ^г Д ^е - дійсні числа, називається

лінійною оболонкою системи векторів з _ХУ ... _у а _т. Позначимо лінійну

оболонку L (o _Xy a _2y ... _y a _m).

Приклади.

1.  Лінійна оболонка векторів базису з _ХУ е ₂ ^е п простору I

збігається з усім простором.

2.  Розглянемо систему функцій 1.x, х * з простору

Їх лінійна оболонка-безліч всіх многочленів ступеня <до •

Легко перевірити, що лінійна оболонка векторів a _xy a _2y ... _y a _m, утворює підпростір, т.к. при додаванні лінійних комбінацій і множенні їх на число знову виходять лінійні комбінації так само векторів.

Для лінійної оболонки L _(a], ..., a _rri) dun L <m, якщо ж a., A _2, ... _y a _m лінійно незалежні, то вони служать базисом в А і dim L = m. Якщо вектори a _x, a _Jy ... _y a _m, породжують лінійну оболонку, лінійно

залежні, то dim L = г, де г - ранг системи векторів (максимальне число лінійно незалежних векторів системи). Всякий базис

L (a _ly ..., a _u) можна доповнити до базису всього простору V. Розглянемо ще один приклад.

У просторі C _(ai) лінійну оболонку 1, {е ^х, е ^х) векторів е \ е ^х

складають функції виду у = ае ^х + Ье ^'х, де а, b - будь-які речові числа. Функції е \ е ¹ лінійнонезалежні і складають базис своєї

лінійної оболонки, dim /, -2. Знайдемо, наприклад, координати гіперболічних функцій y-chx іy-shx в цьому базисі.

Сопремсііав Гун аіігарнзв Академія

/ *, (*) - (5. 9, 2),. Зауважимо, що в стакдзртіом базисі {з} = {і.лг.х *};

многочлен / '(*) - 5 »-'-5д + 7 має координати Р. (*)> ^{7 '5} •