§ 2. Характеристичний многочлен

Нехай - власне число матриці А. Тоді існує вектор , що .

Перепишемо рівність у вигляді

. (*)

Остання векторна рівність являється системою лінійних однорідних рівнянь. Така система завжди має нульовий розв’язок. Нагадаємо, що для того,щоб вектор , задовільний цій системі, був власний, потрібно щоб система (*) мала ненульовий (і, отже, не єдиний) розв’язок. Тоді її визначник

. (**)

Навпаки, якщо визначник однорідної системи (*) дорівнює нулю, то ця система має ненульовий розв’язок, тобто існує власний вектор , відповідний даному .

Отже, має місце теорема. Для того, щоб було власним числом матриці А потрібно и достатньо, щоб

.

Розглянемо рівність (**) детальніше.

Матриця має вигляд:

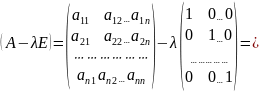
Отже, рівність (**) можна записати так:

Ліва частина цієї рівності є многочленом степені n відносно позначимо його .

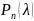Многочлен називається характеристичним многочленом матриці А, а в рівнянні (**) називається характеристичним рівнянням. Нагадаємо , що число є корінь многочлена , і якщо .

Тоді, останню теорему можна сформулювати так :

Теорема. Число власне число матриці А тоді і тільки тоді, коли корінь характеристичного многочлена цієї матриці.

Відомо, що многочлен степені n має рівно n корнів (з урахуванням їх кратності) дійсних або комплексних. Нас буде цікавити тільки дійсні власні числа і відповідні їм власні вектори.

Розглянемо приклад: знайти власні значення і власні вектори матриці

Відповідні власні вектори .

Такі власні числа і вектори ми будемо розглядати.

Отже, наша задача складається у знаходженні дійсних коренів характеристичного многочлена.

В подальшому, говорячи про власні числа, ми будемо мати на увазі тільки дійсні власні числа.

Приклад 1. Знайти власні числа матриці

.

Характеристичний многочлен має вигляд :

.

Характеристичне рівняння:

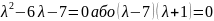
Корні характеристичного многочлена : власні числа матриці А.

Приклад 2. Знайти власні числа матриці

Характеристичний многочлен:

Розкладемо визначник по першому рядку:

Характеристичне рівняння:

Корні характеристичного многочлена: , .

Многочлен має два різні кореня 3,6 при чому корінь 3 кратності 2.

§ 3. Власний підпростір.

Нехай власне число матриці А. Як знайти власні вектори, відповідні даному

Як говорилося, треба дане значення підставити в рівняння (*) и знайти всі розв’язки системи:

(***)

Визначник цієї однорідної системи дорівнює нулю, всі розв’язки такої системи утворюють підпростір простору (див. розділ 1), ненульові вектори якого складають власний підпростір , власних векторів, відповідних даному значенню .

Строго кажучи не є підпростором, так як не містить вектора. Але, коли кажуть про власний підпростір то вектор додається до всіх власних.

Щоб знайти загальний розв’язок системи (***) слід знайти фундаментальну систему розв’язків (ФСР), твірну базис . Нагадаємо, що розмірність підпростору дорівнює n-r, де n – число змінних, r – ранг матриці при даному .

Справедлива теорема.

Теорема. Розмірність власного підпростору не перевищує кратності характеристичного многочлена .

Матриця

Має власні числа . Нехай , тоді система 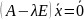приймає вигляд:

Система еквівалентна одному рівнянню , тут n = 2, r = 1, вільна змінна, 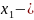залежна. ФСР складається з одного вектора який утворює базис в одновимірному власному підпростору .

Нехай тепер 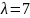, тоді для власного вектора отримаємо систему:

яка еквівалентна одному рівнянню 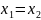. Надаючи вільній змінній значення 1, отримаємо вектор , утворюючий ФСР у власному підпростору

Так яка власне значення , то вектори лінійно незалежні і можуть слугувати базисом простору

Матриця

Має власні числа .

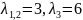Знайдемо власні вектори, відповідні значенню .

Система має вигляд:

Ця система еквівалентна одному рівнянню ,

вільні змінні , залежна.

Загальний розв’язок в координатній формі має вигляд:

.

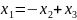Вважаючи 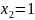, , отримаємо вектор при , отримуємо вектор . Вектори утворюють ФСРв власному підпросторі .

Нехай . Система

Еквівалентна система має вигляд :

n = 3, r =2, , вільна змінна, залежні. Загальний розв’язок в координатній формі: .

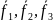При , отримаємо вектор , відображає ФСР власного підпростору . Вектори лінійно незалежні і можуть слугувати базисом простору

Розглянемо іще один приклад.

Характеристичний многочлен :

Власні числа матриці: , . Знайдемо власний підпростір для кратного корня

n = 3, r = 2 , вільна змінна , базис

Зауважимо, що менше кратності кореня . Таким чином, двократному кореню відповідає одномірний власний підпростір .

Нехай тепер , відповідна система має вигляд:

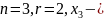вільна змінна, залежні:

і

Хоча лінійно незалежні, але вони можуть створювати базис .

Підведемо підсумки сказаному. Сформулюємо алгоритм пошуку власних числе і власних векторів матриці.

1. Складемо характеристичне рівняння:

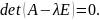
2. Знайдемо дійсні корені характеристичного многочлена (якщо таких немає, то немає і власних векторів). Нехай , де порядок квадратної матриці A.

3. Для кожного кореня складемо система лінійних однорідних рівнянь

і знайдемо її ФСР: , розмірності .

4. Об’єднати знайдені фундаментальні системи по всім власним значенням . Отримана система з власних векторів матриці А буде лінійно незалежною.

ЇЇ число векторів об’єднаної системи то вона утворює власний базис матриці А.