
- •Перелік умінь
- •Тематичний огляд Глава 1. Власні числа та власні вектори матриці § 1. Визначення. Основні властивості власних векторів
- •§ 2. Характеристичний многочлен
- •§ 3. Власний підпростір.
- •Глава 2. Зведення симетричної матриці до діагонального виду § 1. Скалярний добуток в підпросторі . Процес ортогоналізації
- •§ 2. Ортогональна матриця
- •Глава 3. Квадратична форма. Зведення до канонічного виду § 1. Основні визначення. Матриця квадратичної форми.
- •Глава 4. Лінійні простори
- •§ 1. Визначення лінійного простору
- •§ 2. Лінійна залежність
- •§ 3. Базис і координати
- •§ 4. Матриця переходу
- •§ 5. Підпростір
- •§ 6. Евклідові простори
- •Тренінг умінь
- •7. Приклад виконання вправи на вміння № 7. Завдання 1.
- •Рішення
- •Завдання 2
- •Рішення
- •8. Приклад виконання вправи на вміння № 8.
- •Завдання 2
- •Розвязання
- •9. Приклад виконання вправи на вміння № 9.
- •Завдання 2
- •Завдання 3
- •10. Приклад виконання вправи на вміння № 10.
- •Завдання 1
- •Рішення
- •Задание 2
- •Розв’язок
- •Задание
- •Розв’язок
- •Розв’яжіть самостійно наступні задачі
- •Файл матеріалів
- •Перпендикуляр з точки в простір
- •§2 Про наближене обчислення значень матриць
Зміст
ПЕРЕЛІК УМІНЬ 2
ТЕМАТИЧНИЙ ОГЛЯД 6
Глава 1. Власні числа та власні вектори матриці 6
§ 1. Визначення. Основні властивості власних векторів 6
§ 2. Характеристичний многочлен 9
§ 3. Власний підпростір. 11
Глава 2. Зведення симетричної матриці до діагонального виду 15
§ 1. Скалярний добуток в підпросторі . Процес ортогоналізації 15
§ 2. Ортогональна матриця 19
Глава 3. Квадратична форма. Зведення до канонічного виду 23
§ 1. Основні визначення. Матриця квадратичної форми. 23
§ 2. Перетворення матриці при лінійній заміні змінних 24
§ 3. Зведення квадратичної форми до канонічного виду ортогональним перетворенням 24
§ 4. Зведення кривої другого порядку до канонічного виду 24
§ 5. Знаковизначення квадратичної форми. Критерій Сильвестра. 24
Глава 4. Лінійні простори 27
§ 1. Визначення лінійного простору 28
§ 2. Лінійна залежність 29
§ 3. Базис і координати 31
§ 4. Матриця переходу 34
§ 5. Підпростір 37
§ 6. Евклідові простори 39
Глава 5. Лінійні оператори 40
§ 1. Визначення і приклади 40
§ 2. Матриця лінійного оператору 40
§ 3. Самоспряжений оператор 40
ЗАВДАНННЯ ДЛЯ САМОСТІЙНРЇ РОБОТИ 40
ТРЕНІНГ УМІНЬ 48
ФАЙЛ МАТЕРІАЛІВ 68
с,е, +с2е2+- +С„,ет-У- 71
Перелік умінь
№ п/п |
Уміння |
Алгоритм |
1. |
Знаходження власних значень та власних векторів матриці А порядку n |
|
2. |
Побудувати
ортогональну систему векторів
|
|
3. |
Виписати матрицю А квадратичної форми Q(x)=A(x,x), де xєR. Перевірити, буде квадратична форма визначена додатньо (по критерію Сильвестра) |
Тоді матриця квадратичної
форми
Де
Виходить симетрична матриця А.
|
4. |
Привести
квадратичну форму
Q(x)
до канонічного виду ортогональним
перетворенням (xє |
{
y= |
5. |
Привести
центральну криву другого порядку з
центром в початку координат
|
|
6. |
Перевірити утворює лінійний підпростір множину W, в якій визначені операції додавання чи множення на число |
Якщо ZєW , то W - підпростір, інакше – множина W не є підпростором. |
7. |
Вияснити, утворює дана система векторів {f} базис лінійного простору |
Якщо ранг А дорівнює розмірності простору, то система {f} утворює базис, інакше – ні.
|
8. |
Знайти координати вектора x в новому базисі {f}, якщо він заданий в базисі {e} |
|
9. |
Перевірити
лінійність заданого оператора
|
|
10. |
Написати матрицю оператора А в заданому базисі {e} |
|
11. |
Знайти координати образа y=Ax в заданому базисі {e} |
|
|
|
|
12. |
Визначити як змінюється матриця А при переході від базиса {e} до базиса {f} |
|
13. |
В
просторі Р многочленів степеня
|
|

 .
. - власні
числа матриці А.
- власні
числа матриці А. (і=1..n)скласти
системі рівнянь
(і=1..n)скласти
системі рівнянь
 для визначення власних векторів, які
відповідають власному числу
.
для визначення власних векторів, які
відповідають власному числу
. за
заданою лінійно незалежною системою
за
заданою лінійно незалежною системою
 (ортогоналізувати
систему векторів
(ортогоналізувати
систему векторів

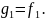
 Отримуємо
ортогональну пару векторів
Отримуємо
ортогональну пару векторів


 лінійні
оболонки системи
{f}
та {g}
співпадають
L(
лінійні
оболонки системи
{f}
та {g}
співпадають
L(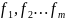 )=L(
)=L( ).
).





 >0,
>0,
 >0,
>0,
 >0,
то квадратична форма визначена додатньо
>0,
то квадратична форма визначена додатньо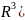 .
. ,
які відповідають власним значенням
.
Вони утворюють базис
,
які відповідають власним значенням
.
Вони утворюють базис
 .
.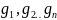
 :
:
 :
:
 .
. }
– ортонормований
власний базис матриці А.
}
– ортонормований
власний базис матриці А.
 .
. .
.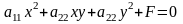 до канонічного виду (попередньо
потрібно перевірити, чи центр знаходиться
в початку координат)
до канонічного виду (попередньо
потрібно перевірити, чи центр знаходиться
в початку координат) ,
де
,
де




 ,
де
,
де
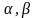 - будь-які числа.
- будь-які числа. по
базису {e}
в
j
–ий стовпчик матриці С.
Отримана
не вироджена матриця є матрицею
переходу С від старого базису
{e}
до нового базису
{f}.
по
базису {e}
в
j
–ий стовпчик матриці С.
Отримана
не вироджена матриця є матрицею
переходу С від старого базису
{e}
до нового базису
{f}. - вектор,
стовпці координат х у відповідних
базисах
- вектор,
стовпці координат х у відповідних
базисах



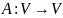



 і записати їх координати в попередньому
базисі
{e}
і записати їх координати в попередньому
базисі
{e} по
базису
{e}.
Отримана матриця А – матриця оператора
А в базисі {e}
по
базису
{e}.
Отримана матриця А – матриця оператора
А в базисі {e} координат х в базисі і визначити
координати
координат х в базисі і визначити
координати
 вектора у в базисі {e}:
вектора у в базисі {e}:
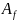 в базисі
{f}
в базисі
{f}

 задана
система векторів
задана
система векторів
 ,
і перетворення А. Пересвідчитись, що
{f}-
базис, оператор А – лінійний, написати
матриці оператора А в базисах
{e}
,
{f},
де {e}
- стандартний базис.
,
і перетворення А. Пересвідчитись, що
{f}-
базис, оператор А – лінійний, написати
матриці оператора А в базисах
{e}
,
{f},
де {e}
- стандартний базис.