4 Анализ модели на чувствительность

Проведем анализ на чувствительность задачи линейного программирования, рассчитанной выше. Для этого, построим двойственную задачу по отношению к исходной:

При решении прямой задачи было получено оптимальное решение . Решим двойственную задачу по УДН:

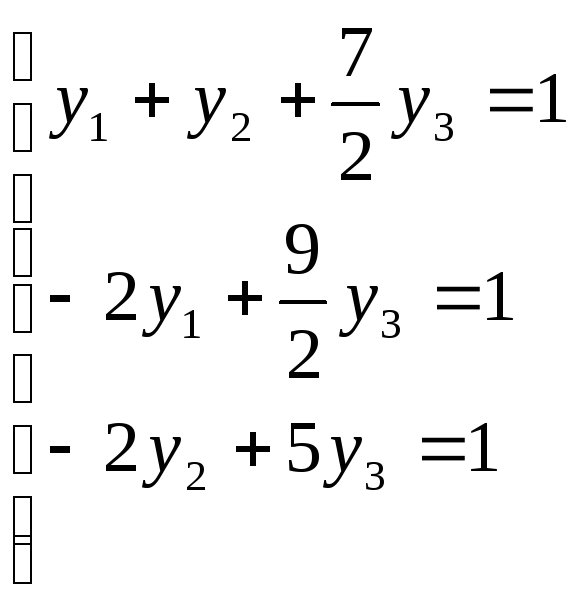
Оптимальные значения целевых функций взаимно-двойственных задач равны:

.

Ресурсы b₁иb₂всегда равны нулю, так как именно такая запись ограничений обеспечивает выполнение необходимого ассортимента распила. Проанализируем, каким образом изменение ресурсаb₃повлияет на изменение целевой функции. Другими словами, выясним, как необходимо изменять данный ресурс, для увеличения целевой функции.

Необходимо найти такие , чтобы при подстановкев прямую задачу было получено также оптимальное решение (с учетом заданного ассортимента), но уже с большей целевой функцией.

Ввиду того, что заданный ассортимент (2:1:1) предполагает длину бревна не менее 16,5 метров (2·3,5+1·4,5+1·5 = 16,5), примем В этом случае

Решим прямую задачу с учетом указанных изменений:

.

Проанализировав полученное решение и сопоставив его с условиями задачи, был сделан вывод – для увеличения целевой функции (числа брусьев в заданном ассортименте) ресурс b₃необходимо использовать в размере не менее 33 метров. Приb₃ < 33 распил бревна в ассортименте 2:1:1 невозможен.

b₃= 33 +,

где =33·n,n=, 1, , 2, , ... .

Тогда f(x)= 12, 16, 20, 24, 28, ... .

4, 8, 12, 16, 20, ... .

Заключение

В ходе проделанной работы, по условиям исходной задачи, была составлена математическая модель, реализующая цель проведения оптимизации, а именно: максимизацию числа брусьев в заданном ассортименте. Для демонстрации корректной работы составленной модели, ее численная реализация была представлена в расчетной части пояснительной записки. Для выявления возможных способов улучшения работы данной модели, был проведен анализ на чувствительность. В данной расчётно-графической работе по заданному условию задачи была составлена математическая модель и произведён расчёт задачи на примерных данных с помощью прямого симплекс-метода, целью оптимизации была минимизация затратности производства костюмов.

Список использованных источников

1. Зыкина А.В. Математическое программирование: Учеб. пособие. Омск: Изд-во ОмГТУ, 2000. 64 с.

2. Зайченко Ю.П. Исследование операций. - Киев: Высшая школа, 1979.

3. Дегтярев Ю.И. Введение в исследование операций. - М.: Высшая школа, 1986. – 224с.

4. Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, и др.; Под ред. Н.Ш. Кремера. Исследование операций в экономике: Учеб. пособие для вузов. – М.: ЮНИТИ, 2000.- 407 с.

16