В) Оценка точности измерений по формуле ф. Бесселя ( по вероятнейшим уклонениям )

При выполнении измерений истинное значение измеряемой величины, как правило, неизвестно. В этом случае ср.кв.ош. отдельного измерения вычисляют по вероятнейшим уклонениям V измеренных величин от их среднего арифметического .

Формулу для оценки результатов измерений по вероятнейшим уклонениям вывел немецкий астроном Ф. Бессель, которая представляется в виде

m = = , ( 10 )

где V_i - уклонение отдельных измерений l _i от их среднего арифметического l _ср ( V_i = l _i - l _ср );

n - число измерений.

Среднюю квадратическую ошибку М среднего результата измерения

в этом случае вычисляют по формуле

М = . ( 11 )

Пример обработки результатов измерения длины линии приводится в таблице 2.

Таблица 2 Обработка результатов измерений по формуле Ф. Бесселя

№ № Измеренная

измерений величина, V_i, см V² _i,см

l _{i ,} м

1 125.10 0 0

2 125.12 + 2 4

3 125.08 - 2 4

4 125.08 - 2 4

5 125.12 + 2 4

n = 5 l ср = 125.10 м =0 =16

m = 2 см , М = 0.9 см.

Д) Оценка точности измерений по разностям двойных измерений

При выполнении топографо-геодезических работ одну и ту же величину часто измеряют дважды. Например, длины сторон теодолитного хода измеряют землемерной лентой прямо и обратно, горизонтальные углы - двумя полуприёмами и т.д. В этом случае оценку точности результатов измерений выполняют по разностям двойных измерений. При этом, если оценивают точность определения одной разности из всей совокупности измерений, то вычисляют её среднюю квадратическую ошибку m _{d i} из соотношения, близкого по своему смыслу к формуле К. Гаусса, т.к. истинные ошибки разностей равны нулю

m _{d i} = = , ( 12 )

где d _i - разности двойных измерений l _{1 ,} l _;

n - число двойных разностей .

Каждая разность образована как d _i = l ₁ - l ₂. Поэтому ср.кв.ош. одной разности d выражается формулой m ²_d = m ²_l + m²₂ . Так как измерения l равноточны, то m _l = m ₂ = m _l . Следовательно, m² _d = 2 m² _l. Отсюда m _d = m _l , а

m _l = m _d / . ( 13 )

Подставив в формулу ( 12 ) соотношение для m _d ( 11 ) , получим выражение для ср.кв.ош.. m _l отдельного измерения l _i по разностям двойных измерений

m _{l i} = . ( 14 )

Из разности двойных измерений l ₁ и l ₂ обычно берут среднее значение

l ср. = , ( 15 )

тогда согласно формуле ( 13 )

m _{l ср.} = . ( 16 )

Подставляя в формулу ( 16 ) выражение ( 14 ) для m _l , получим формулу для оценки точности среднего арифметического из всей совокупности измерений по разностям двойных измерений

m _{l ср.} = . ( 17 )

Приведенные формулы ( 12 ), ( 14 ), ( 17 ) справедливы для случая, когда разности двойных измерений являются случайными ошибками ( свободны от систематических ошибок ), т.е. тогда, когда выражение = 0 или близко к нулю. Если это выражение заметно отличается от нуля, то формулы, приведенные выше для оценки точности результатов измерений по разностям двойных измерений, применять нельзя.

В этом случае необходимо определить систематическую ошибку по формуле

= ( 18 )

и исключить её из каждой разности двойных измерений, вычислив величины по формуле

= d _i - . ( 19 )

Значения ошибок являются по существу уклонениями разностей d _i от их арифметической средины , т.е. являются вероятнейшими ошибками. Следовательно, для оценки точности измерений по результатам двойных измерений может быть применена формула Бесселя.

В этом случае ср.кв.ош. определения одной разности m _{d i} из всей совокупности двойных измерений определяют по формуле

m _{d i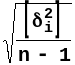} = . ( 20 )

Средние квадратические ошибки определения отдельного результата измерения m _{l i} и среднего арифметического m _{l ср.} из всей совокупности измерений вычисляют из соотношений

m _{l i} = , ( 21 )

m _{l ср.} = . ( 22 )