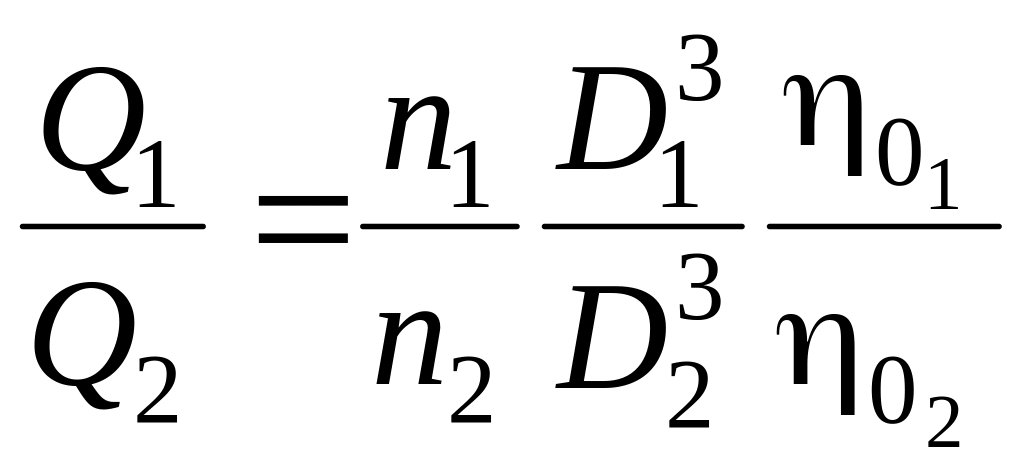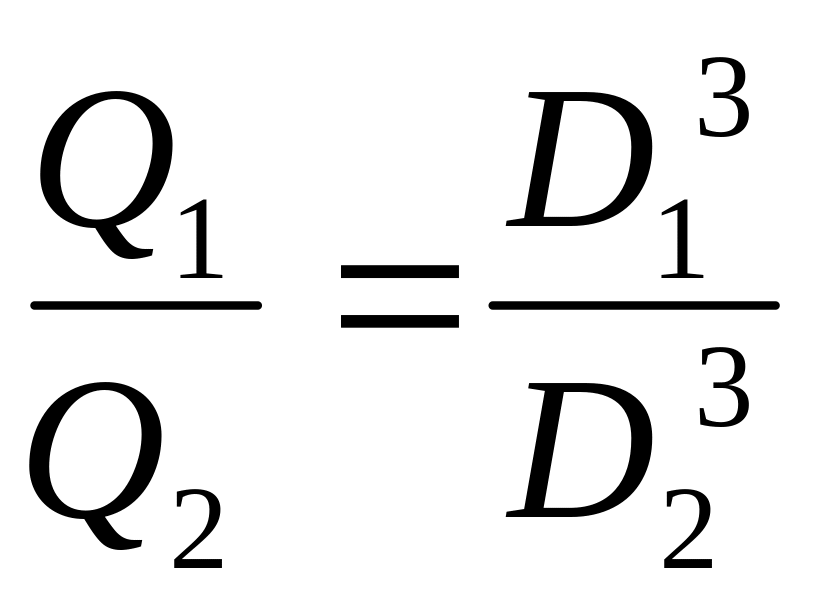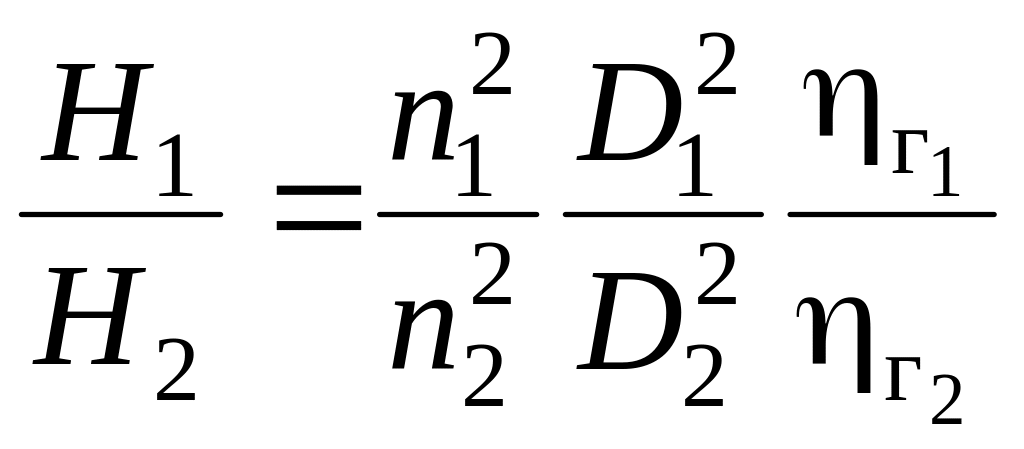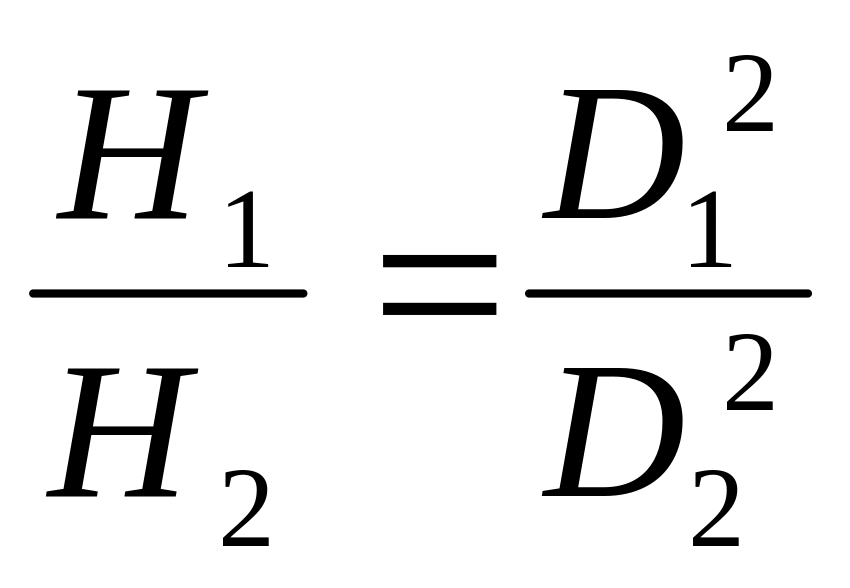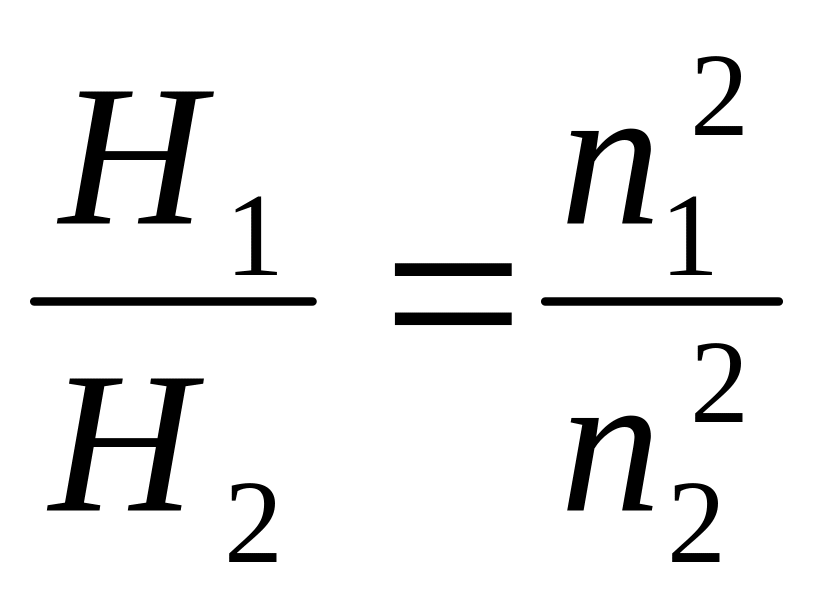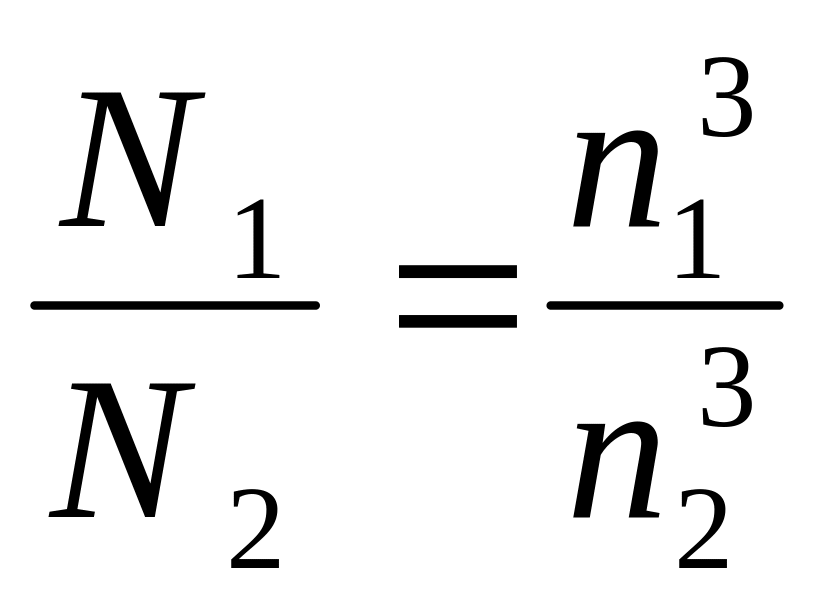9.8. Основы теории подобия лопастных насосов

Полученные уравнения (9.49) и (9.50) лопастных насосов позволяют по заданным расходам и числу оборотов рассчитать и спроектировать рабочее колесо насоса, а стало быть, и сам насос. Однако эти уравнения не учитывают, или недостаточно точно учитывают (9.51) и (9.52) ряд факторов - неравномерность распределения скорости, гидравлические и объёмные потери и т.д. Могут быть и определённые неточности при изготовлении насоса. Поэтому действительные значения подачи и напора будут несколько отличаться от расчётных и для их определения необходимы лабораторные исследования. Исследования проводятся на моделях. Для перехода от данных, полученных на моделях, к реальным параметрам насосов используется теория подобия.

Общие положения теории подобия справедливы, разумеется, и для лопастных насосов.

Два насоса будут подобны, если выполняются следующие условия:

1. Геометрическое подобие насосов - равенство сходственных углов и постоянство отношений сходственных размеров. Оно включает в себя подобие:

а) формы каналов насосов;

б) шероховатости стенок каналов;

в) зазоров в щелевых уплотнениях;

г) толщину лопастей рабочего колеса.

2. Кинематическое подобие - постоянство отношений скоростей в сходственных точках геометрически подобных машин, т.е.

, (9.58)

где н - обозначает параметры, относящиеся к натурному насосу; м - к модели.

3. Динамическое подобие - постоянство отношений сил одинаковой природы, действующих в сходственных точках геометрически и кинематически подобных машин. Динамическое подобие напорных установившихся потоков требует равенства чисел Re, которые у лопастных насосов обычно записываются в виде:

. (9.59)

Режимы работы геометрически подобных насосов, при которых выполняются второе и третье условия, называются подобными.

Предположим, что две подобные машины с радиальным входом работают в подобных режимах. Тогда в соответствии с первым условием

. (9.60)

Окружная скорость связана с числом оборотов в секунду рабочего колеса соотношением

, (9.61)

так как U = R, а угловая скорость  = 2/t = 2n, где [] = рад/с; [n] = об/с; [R] = M; [U] = м/с.

С учётом соотношения (9.58) можно записать:

. (9.62)

Подача рабочего колеса насоса определяется соотношением (9.55):

.

Подача Q насоса меньше Q_к на величину объёмных потерь, которые учитываются объёмным КПД насоса (9.20):

.

Отношение подачи натурного и модельного насосов с учётом равенства _2н = _2м и формул (9.60), (9.62) будет:

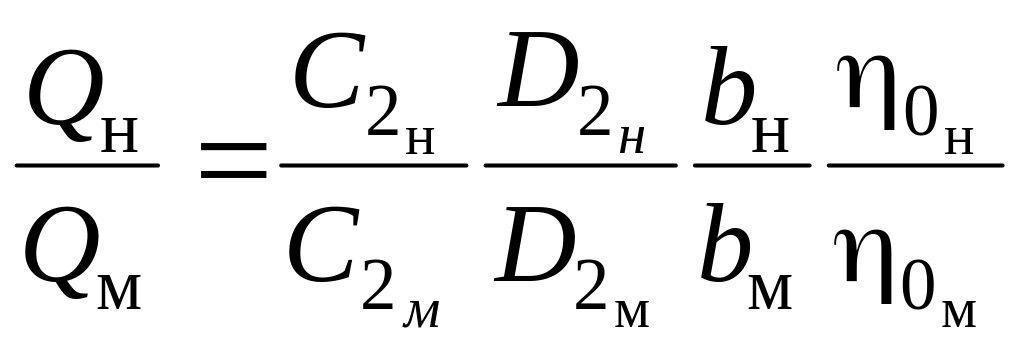. (9.63)

При _но = _мо получим . (9.64)

Теоретический напор (9.50) равен:

,

а действительный напор (9.51):

.

Для подобных насосов число лопастей и их относительная толщина одинаковы и _zн = _zм.

Тогда 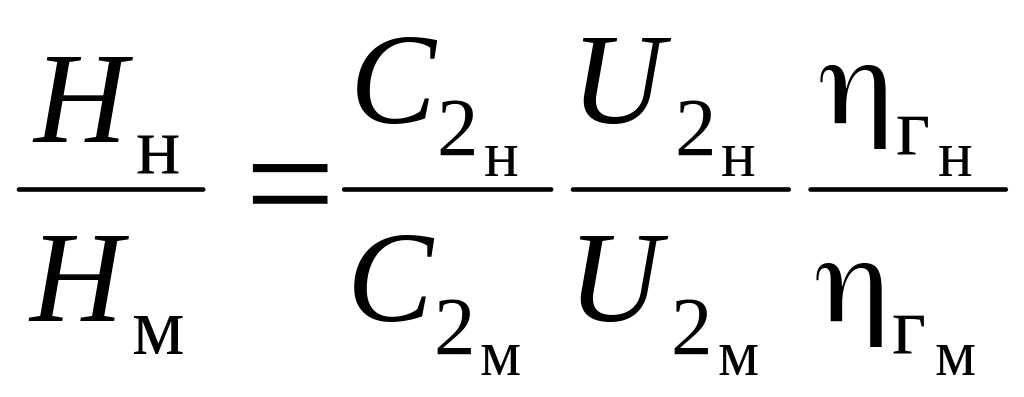. (9.65)

Гидравлические КПД натурного и модельного насосов обычно близки, т.е. _гн = _гм и формулу (9.65) можно записать так:

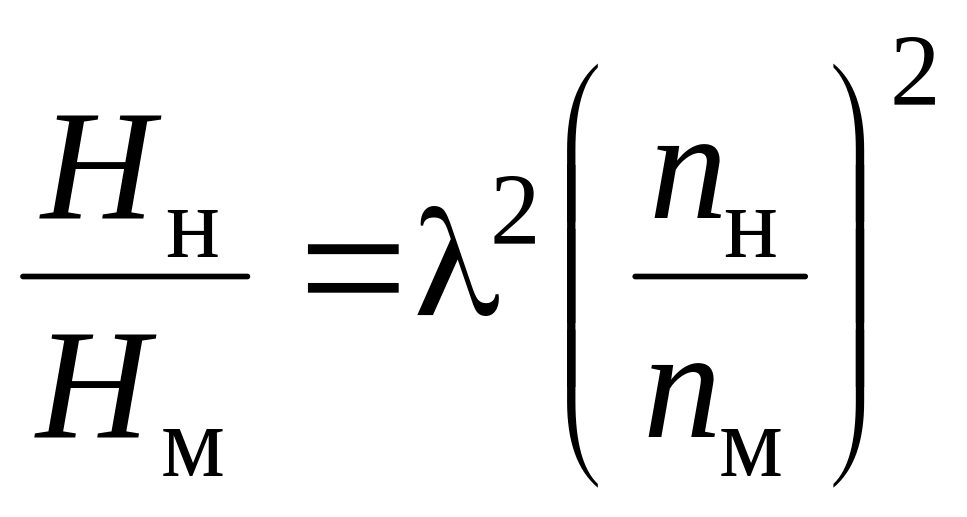. (9.66)

Потребляемая насосом мощность (9.12):

и соотношение потребляемой мощности натурного и модельного насосов будет равно:

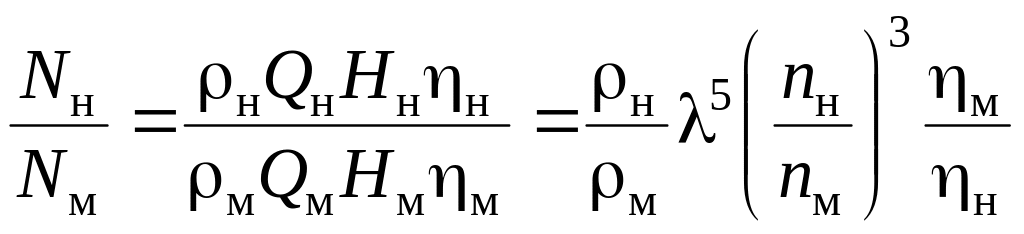. (9.67)

Если натурный и модельный насосы перекачивают одну и ту же жидкость (_н = _м ), а полные КПД насосов близки (_м  _н), то

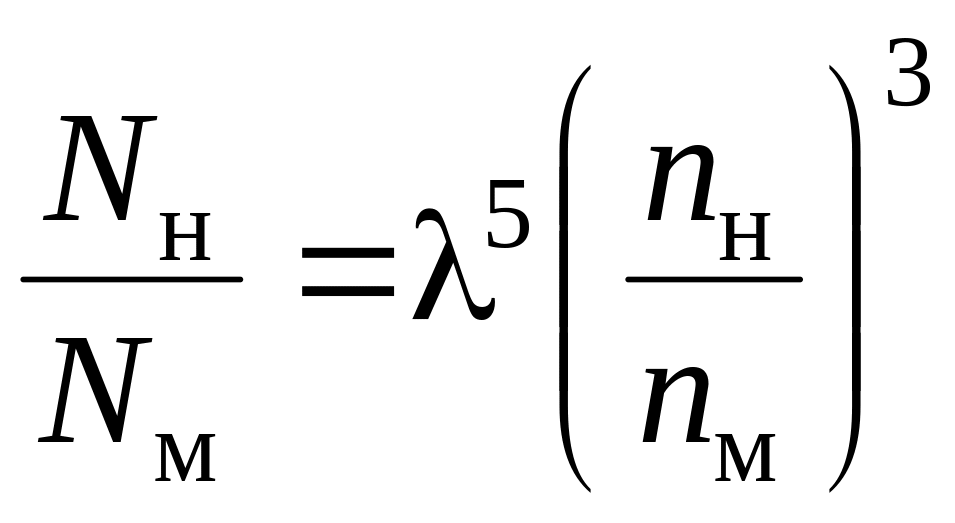. (9.68)

Полученные соотношения (9.64) - (9.68) устанавливают связь рабочих параметров подобных насосов с их масштабом и числом оборотов рабочего колеса, т.е. устанавливают законы подобия.

Законы подобия позволяют получить зависимость подачи, напора и мощности центробежного насоса от числа оборотов, т.е. соотношения подобия для одного и того же насоса (_н = _м).

Из формул (9.64), (9.66) и (9.68) получим:

; (9.69)

; (9.70)

. (9.71)

Зависимости (9.69) - (9.71) используются для пересчёта характеристик насоса с одного числа оборотов на другое. Отметим, что при изменении числа оборотов n меняется напор H, подача Q, значения скоростей C, w, U.

Это вызывает изменение потерь напора _г, перетечек жидкости _о и полного КПД  насоса. Поэтому полученные законы пропорциональности (9.69) - (9.71) достаточно точно выполняются при небольших изменениях n (20 - 40 %), а при больших изменениях n точность несколько уменьшается.

Для удобства использования законов подобия сведём их в табл. 9.3 с учётом изменяющихся (var) и постоянных (const) параметров двух подобных насосов.

Таблица 9.3

D, n, ,  - var	 - const
	 - var D, n - const	D - var n, - const	n - var D, - const