Глава 8. Особенности гидравлического расчета газопроводов

8.1. Уравнение неразрывности и уравнение Бернулли для газа

Перекачка по трубам газов имеет весьма широкое применение, в том числе и в установках газового пожаротушения. По сравнению с движением жидкостей движение газов характеризуется рядом особенностей, обусловленных различием физических свойств жидкостей и газов, сжимаемостью газов.

Так как при изменении давления плотность газа меняется существенно, то уравнение неразрывности (2.11) должно использоваться для массового расхода жидкости

, (8.1)

т.е. масса газа, протекающего в единицу времени через любое живое сечение потока (или элементарной струйки), постоянна.

При выводе уравнения Бернулли для элементарной струйки идеальной жидкости было получено:

.

Для газов плотность вносить под знак дифференциала нельзя, так как при течении сжимаемого газа надо учитывать  = f(p). При движении реальных газов, обладающих вязкостью, следует учитывать потери напора и уравнение Бернулли примет вид:

. (8.2)

Интегрируя уравнение (8.2) по длине от некоторого сечения I-I до сечения II-II, получим:

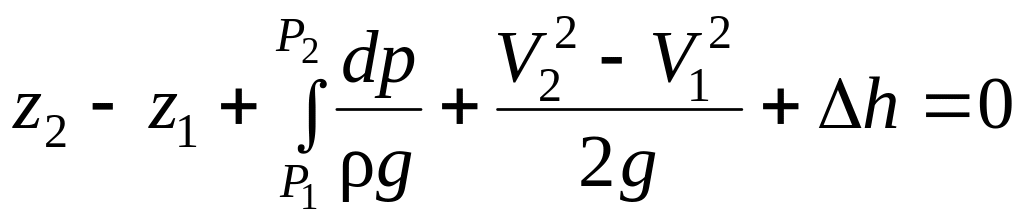. (8.3)

Уравнение состояния газа выражает зависимость между абсолютным давлением p, плотностью  и абсолютной температурой T:

, (8.4)

где R - газовая постоянная, равная универсальной газовой постоянной R = 8314 Дж/(кмольград), поделенной на массу M одного киломоля данного вещества

, Дж/(кгград). (8.5)

Значения газовой постоянной для некоторых веществ приведены в табл. 8.1.

При политропическом процессе

или 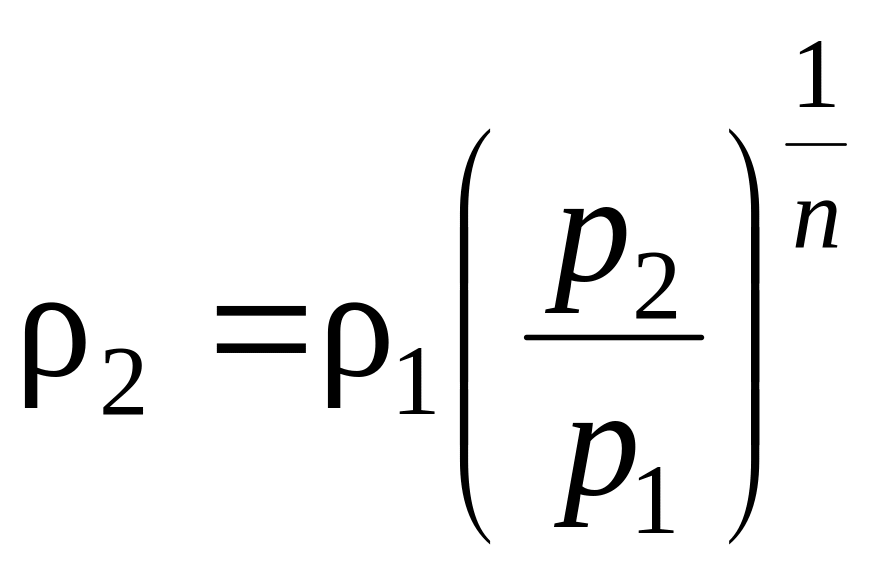. (8.6)

Таблица 8.1

Вещество	Химическая формула	R, Дж/(кгград)
Водяной пар	Н2О	461,5
Азот	N2	296,8
Двуокись углерода	СО2	189,9
Окись углерода	СО	296,8
Воздух		287,0

Подставляя уравнение (8.6) в уравнение (8.3), после преобразований получаем:

. (8.7)

В уравнении (8.7) величина называется температурным напором.

Таким образом, в установившемся движении газа величина полного напора равна сумме геометрического, пьезометрического, скоростного и температурного напоров.

При адиабатическом процессе (нет теплообмена) в уравнении (8.7) вместо показателя политропы n следует подставить показатель адиабаты k.

Если температура газа при течении не меняется (изотермический процесс, Т = const),то из уравнения (8.4) следует:

,

и уравнение Бернулли примет вид:

.

8.2. Расчет газопроводов при малых перепадах давления

Под малым перепадом давления обычно понимается величина

где p = p₁ - p₂ - изменение давления вдоль трубопровода на рассматриваемом участке, - среднее значение давления на этом участке.

Сжимаемостью газа обычно пренебрегают, если скорость его движения менее четверти скорости звука (V < 0,25 V_зв). Например, для воздуха при обычных (20 ^оС) температурах V < 85 м/с. В системах вентиляции, в некоторых случаях работы установок газового тушения сжимаемостью газов можно пренебречь и считать плотность транспортируемого газа неизменной по всей длине трубопровода. Тогда расчеты воздуховодов и газопроводов принципиально не отличаются от расчетов несжимаемых жидкостей и уравнением Бернулли (8.7) можно пользоваться как и для несжимаемой жидкости без учета температурного напора.

При расчете газопроводов обычно рассматривается изменение давления, а не напора. Поэтому уравнение Бернулли преобразуем, умножив правую и левую часть на g. С учетом того, что gh = P_п можно записать

. (8.8)

В большинстве случаев изменением весового давления газа можно пренебречь, так как вследствие малой плотности газа эта величина мала по сравнению с другими членами уравнения.

. (8.9)

Если d = const, то и . (8.10)

Потери давления складываются из линейных и местных:

, (8.11)

где n - число линейных участков, m - число местных сопротивлений. Формулы для определения линейных и местных потерь давления имеют вид:

или (8.12)

или . (8.13)

Величина называется динамическим давлением.

Средняя плотность газа определяется по среднему давлению из уравнения состояния (8.4). Формулы (8.9) – (8.13) идентичны формулам для несжимаемой жидкости. Коэффициенты  и  в формулах (8.12) и (8.13) определяются по тем же формулам и таблицам, что и для несжимаемой жидкости. При этом надо помнить, что эти коэффициенты зависят от режима движения, определяемого числом Рейнольдса:

,

где V - скорость газа, м/с,  - кинематическая вязкость газа, м²/с.