3.4. Примеры использования уравнения бернулли при решении задач пожарной практики

Применение некоторых приборов и устройств в пожарной практике основано на знании уравнения Бернулли. Далее приводятся несколько примеров применения уравнения Бернулли в этой области.

Ствол-водомер

Ствол-водомер используется для измерения расхода воды, проходящей по рукавным линиям. Он состоит из собственно ствола 1 с манометром 2 и насадка 3 (рис. 3.4).

2

1

2

Рис. 3.4. Ствол-водомер

В качестве плоскости сравнения выбираем горизонтальную плоскость, проходящую через ось ствола. Сечение I-I выбирается в месте присоединения манометра, а сечение II-II совпадает с выходным сечением насадка. В уравнении Бернулли

,

,

где p_ман - показания манометра; , так как p₂ = 0 - избыточное давление на выходе из насадка при истечении в атмосферу.

Потери напора h_1-2 можно приближенно считать равными потерям напора в насадке и выразить через коэффициент местного сопротивления в насадке

.

Скорость V₁ можно, воспользовавшись уравнением неразрывности (2.12), выразить через скорость V₂

.

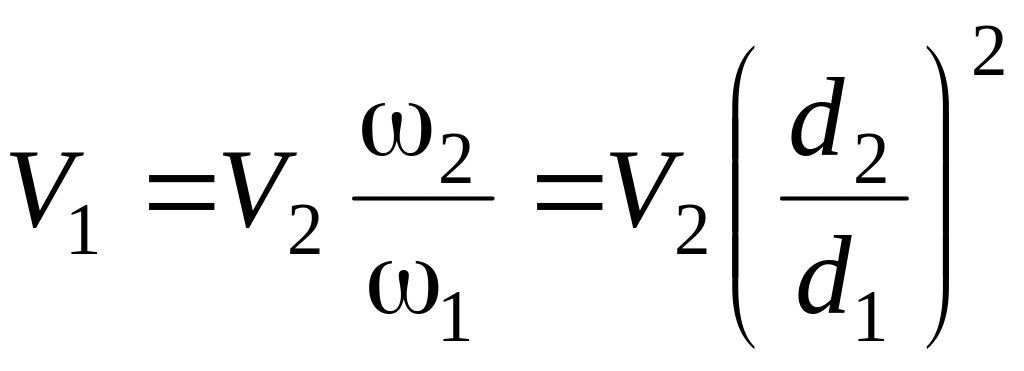Уравнение Бернулли приводится к виду

,

отсюда 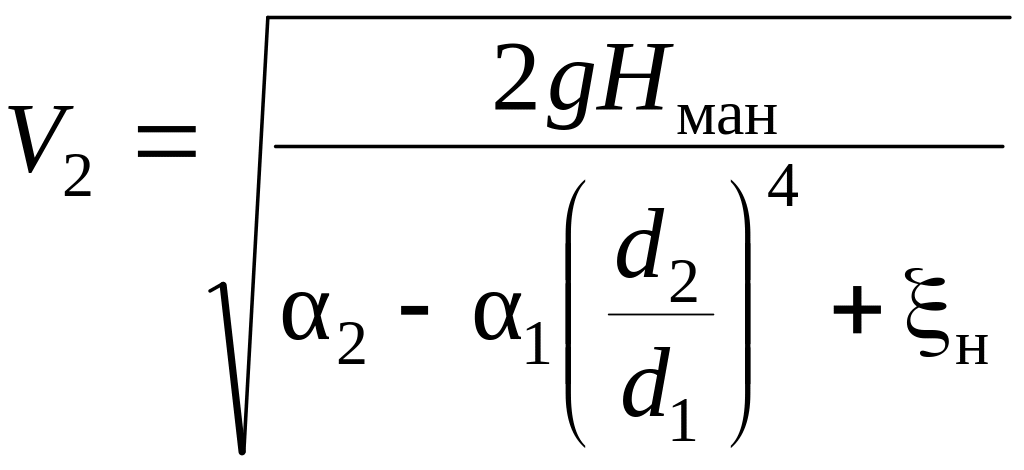. (3.15)

Расход воды определяется из соотношения

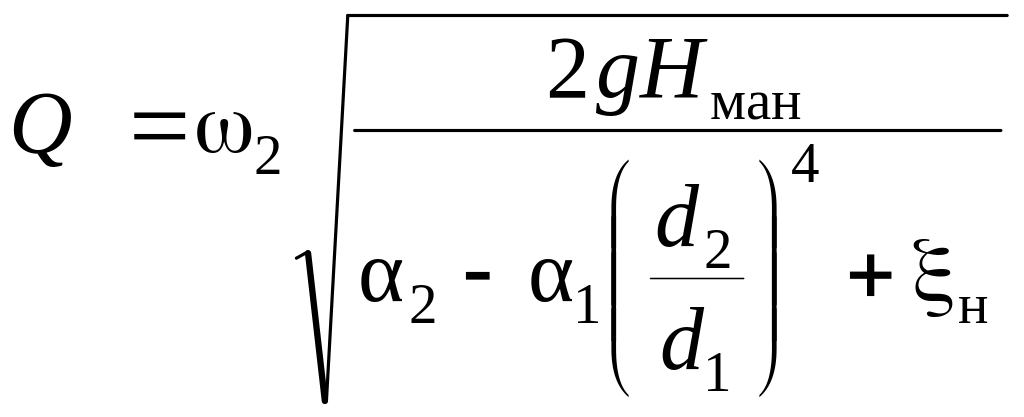. (3.16)

Обозначим комплекс .

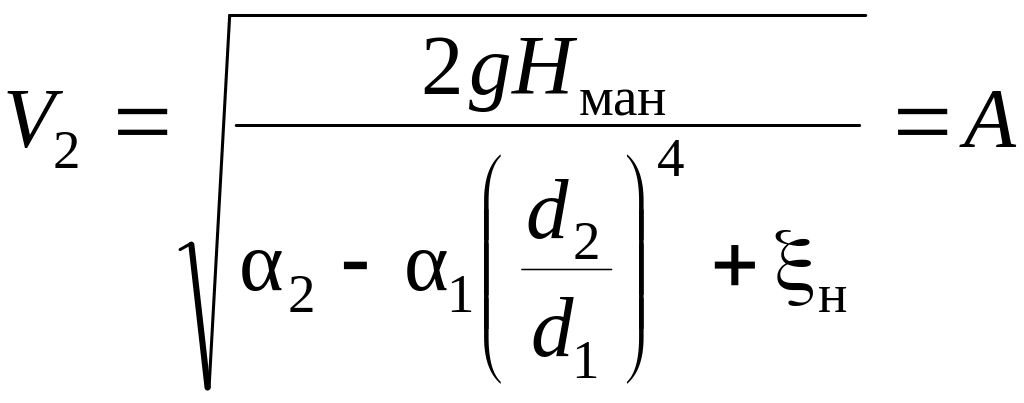Эту величину для данного ствола-водомера можно считать постоянной, тогда соотношение (3.16) записывается в следующем виде:

. (3.17)

Если использовать непосредственное показание манометра р_ман, то с учетом соотношения р_ман = gH формула (3.17) приобретает вид

, (3.18)

обозначив , получим . (3.19)

Струйные аппараты

Струйные аппараты нашли широкое применение в различных областях техники. Они представляют собой устройство, которое позволяет подсасывать и поднимать на определенную высоту жидкость, порошок или другую рабочую среду. Достоинством струйных аппаратов является простота их устройства и безопасность в работе, что в какой-то мере искупает их основной недостаток - низкий коэффициент полезного действия, составляющий 25 %. В пожарной технике наиболее широко используются водоструйные аппараты, в которых рабочей средой, подводимой к аппарату, является вода, а эжектируемой - порошок, пенообразователь или вода (у гидроэлеваторов).

Принципиальное устройство водоструйного аппарата показано на рис. 3.5. Он состоит из следующих основных элементов: рабочего насадка 1, приемной камеры 2, камеры смешения 3, диффузора 4. Принцип действия аппарата состоит в следующем: рабочая жидкость с расходом воды Q₁ проходит через насадок, на выходе из которого в результате увеличения скорости давление падает и в приемной камере образуется разряжение, за счет которого создается подсасываемый поток Q₂.

Максимальное значение разряжения наблюдается на входе в камеру смешения. В диффузоре давление увеличивается. Струйный аппарат рассчитывается с использованием уравнений Бернулли для сечений I-I и II-II, III-III и IV-IV, V-V и VI-VI.

Для сечений I-I и II-II уравнение Бернулли имеет вид

. (3.20)

1

2

II

II

I

I

III

III

IV

IV

V

V

4

VI

VI

Q₂

_атм

_атм

Рис. 3.5. Схема водоструйного аппарата и примерное

распределение давления по его длине

В сечении I-I давление всегда избыточное, а в сечении II-II - вакуум. Тогда соотношение (3.20) перепишется в виде

. (3.21)

С учетом уравнения неразрывности потока жидкости

,

. (3.22)

Аналогичные соотношения получаются при использовании уравнения Бернулли для сечений III-III и IV-IV, V-V и VI-VI. Такая система уравнений позволяет связать между собой рабочие и геометрические параметры эжектора Q₁, Q₂, p₁, p₆, d₂, d₃. Обычно параметрами Q₁, Q₂, p₁, p₆ задаются, а значения d₂, d₃ находятся. Подробности расчета струйных аппаратов можно найти в специальной литературе, например [8, 9].