3.3. Уравнение бернулли для потока реальной жидкости при установившемся плавноизменяющемся движении

Рассмотрим установившееся плавноизменяющееся движение потока реальной жидкости. Каждая элементарная струйка в данном живом сечении потока имеет удельную энергию, т.е. энергию, отнесенную к весу жидкости в этой струйке

. (3.6)

Абсолютная энергия жидкости, проходящей в единицу времени через все живое сечение  потока жидкости, определяется интегрированием выражения (3.6) по сечению потока

.

Удельная энергия потока, т.е. полная энергия, отнесенная к весу жидкости, проходящей через живое сечение  в единицу времени, определится выражением

. (3.7)

С учетом соотношений (3.5) и (2.9) получается

. (3.8)

Преобразуем 2-й член соотношения (3.8)

,

где 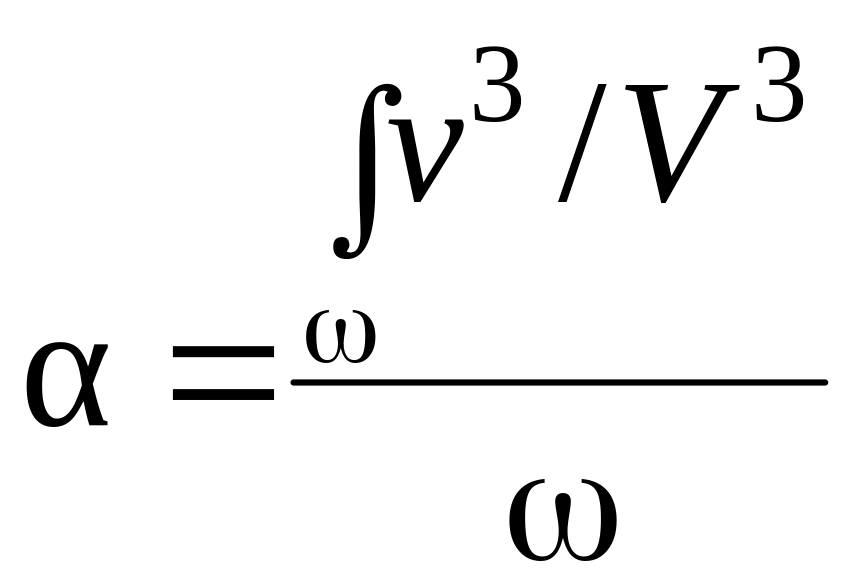- коэффициент Кориолиса.

Безразмерный коэффициент α представляет собой отношение действительной кинетической энергии массы жидкости, протекающей в единицу времени через живое сечение, к условной кинетической энергии, вычисленной, исходя из предположения, что скорости во всех точках живого сечения равны средней скорости. Коэффициент α всегда больше единицы. При ламинарном режиме движения в круглых трубах  = 2, а при турбулентном  = 1,1-1,15. Так как в большинстве случаев в пожарной практике имеют дело с турбулентным режимом, то в расчетах можно приближенно принимать  = 1.

Таким образом, полная удельная энергия потока реальной жидкости в любом сечении равна

.

Вследствие действия сил трения полная удельная энергия жидкости в направлении движения уменьшается. Поэтому для двух сечений I и II, из которых сечение II находится за сечением I в направлении движения жидкости, можно записать

. (3.9)

Величина h_1-2 называется потерей напора или потерей полной удельной механической энергии жидкости при движении от сечения I-I до сечения II-II. Уравнение (3.9) называется уравнением Бернулли для потока реальной жидкости. На риc. 3.3, аналогичном рис. 2.4, показаны пьезометрическая линия и напорная линия для потока реальной жидкости. В отличие от рис. 2.4 на рис. 3.3 напорная линия не является горизонтальной, а снижается в направлении движения жидкости.

Рис. 3.3. Иллюстрация уравнения Бернулли для потока реальной жидкости

При движении реальной жидкости от сечения I-I к сечению II-II (см. рис. 3.3) снижение напорной линии выражает собой потери напора. Потери напора (энергии) h_1-2, отнесенные к длине, на которой эти потери имеют место, называют средним гидравлическим уклоном, т.е.

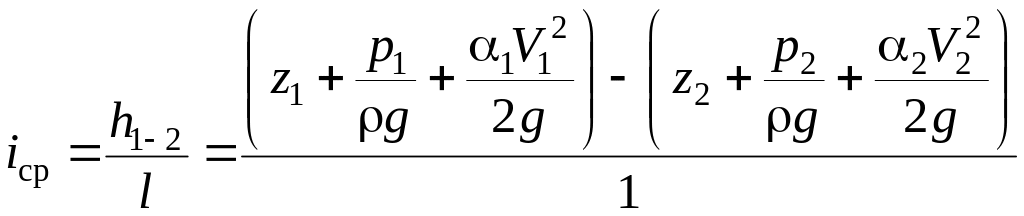. (3.10)

Гидравлический уклон в дифференциальном виде записывается следующим образом:

. (3.11)

Так как всегда dh > 0 и dl > 0, то i > 0.

С другой стороны, соотношение (3.11) может быть записано в виде

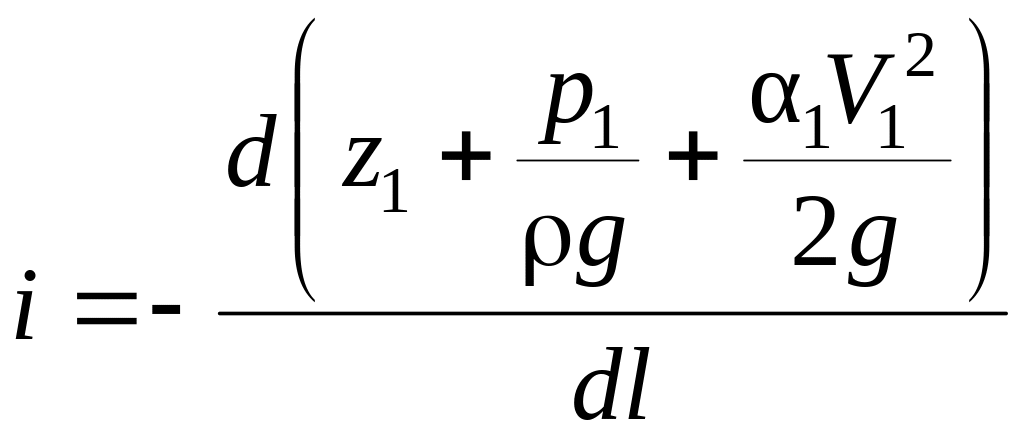. (3.12)

Знак минус в выражении (3.12) показывает то, что полная удельная энергия в направлении движения жидкости убывает, т.е.

.

Для того чтобы выполнялось соотношение i > 0, ставится знак минус. Изменение пьезометрического напора z + p/g, отнесенное к длине, на которой происходит это изменение, называется средним пьезометрическим уклоном

. (3.13)

Пьезометрический уклон в дифференциальном виде имеет вид

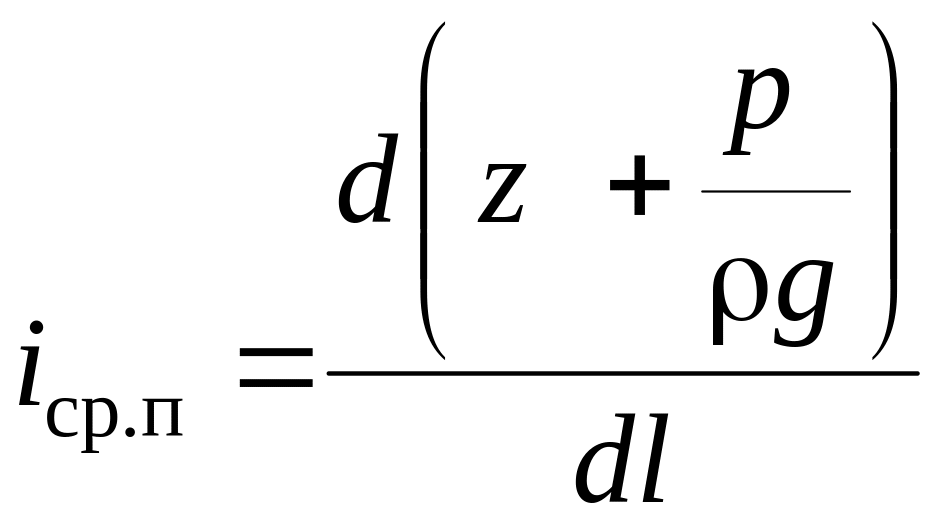. (3.14)

В отличие от гидравлического уклона пьезометрический уклон может быть как положительным, так и отрицательным. Если пьезометрическая линия снижается в направлении движения жидкости, то пьезометрический уклон положительный, а если повышается, то отрицательный. При использовании уравнения Бернулли для решения задач следует иметь в виду, что при этом должны выполняться следующие условия:

1. Расход жидкости между сечениями I-I и II-II должен быть постоянным.

2. Движение жидкости должно быть установившимся.

3. Движение жидкости в сечениях I-I и II-II должно быть равномерным или неравномерным, но плавноизменяющимся; в промежутке между сечениями движение может быть и резкоизменяющимся.

Решение задач с использованием уравнения Бернулли для потока реальной жидкости выполняется по методике, изложенной в разд. 3.4.