Реферат по теме: ''Применение определённого интеграла в экономике''

Лапковская Д.В. 14 БД-2

История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи на вычисление площадей. Латинское слово quadratura переводится как “придание квадратной формы”. Необходимость в специальном термине объясняется тем, что в античнoe время еще не были достаточно развиты представления о действительных числах. Математики оперировали с их геометрическими аналогами или скалярными величинами, которые нельзя перемножать. Поэтому и задачи на нахождение площадей приходилось формулировать, например, так: «Построить квадрат, равновеликий данному кругу». (Эта классическая задача “о квадратуре круга” круга» не может, как известно, быть решена с помощью циркуля и линейки.) Символ т введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa) Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integro, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина интеграл иное: слово integer означает целый. В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и название новой ветви математики -интегральное исчисление (calculus integralis ), которое ввел И. Бернулли. Другие известные термины, относящиеся к интегральному исчислению, появились заметно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее «примитивная функция», которое ввел Лагранж (1797 г.).

Применение понятия определенного интеграла в экономике Производительность труда

 

Пусть   описывает изменение производительности некоторого производства с течением времени.

Найти объем продукции Q, произведенной за промежуток времени  .

Допустим, что производительность труда не изменяется с течением времени, тогда объем продукции ∆Q, произведенный за период времени  , задается формулой  . В общем случае справедливо приближенное равенство  , где  , которое становится более точным при уменьшении ∆t.

Разобьем отрезок   на промежутки времени точками:  . Для объема продукции ∆Q, произведенной за период времени  , имеем  , где  ,  ,  . Тогда сумму приближенных равенств:

,

каждое из которых становится более точным при:

,

 запишем в виде:

.

Согласно определению определенного интеграла получим

.                                       (1)

В последнем равенстве   - производительность труда в момент t, а   - объем выпускаемой продукции за промежуток времени  .

Заметим, что в производственной функции Кобба - Дугласа затраты труда можно принять за линейную зависимость от времени и при этом считать затраты капитала неизменными. Тогда функция примет вид  , а объем выпускаемой продукции за  Т лет составит:

.                                                    (2)

Пример 1. Найти объем продукции, произведенной за 4 года, если функция Кобба - Дугласа имеет вид  .

Решение. По формуле

объем произведенной продукции

.

Используем метод интегрирования по частям.

Пусть  , . Тогда

,  .

Следовательно:

.

 

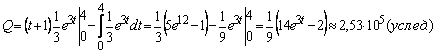Кривая обучения

Пусть   - время, измеряемое в человеко-часах, необходимое для производства первых х ед. продукции.

Найти время, необходимое для производства единиц продукции с номерами от   до n₂.

Рис. 1

Выражение   приближенно равно значению времени, необходимого для производства  -й единицы продукции. Как правило, используют функции вида  , где  ,  . График функции такого вида представлен на рис. 1 и называется кривой обучения.

Заметим, что функция   - убывающая, так как время, необходимое для выполнения операции, убывает при возрастании числа повторов.

Время  , необходимое для производства единиц продукции с номерами от   до n₂, вычисляется по формуле

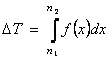.                                                                       (3)

Пример 2. После сборки 100 часов оказалось, что в дальнейшем время убывает в соответствии с формулой   Найти время, которое потребуется для сборки еще 20 часов (т.е. с номера 101 до номера 120).

Решение. В соответствии с формулой

можно записать изменения времени:

 

Средние значения

Пусть функция   показывает изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства, где х - порядковый номер изделия в партии.

Среднее время t_ср, затраченное на изготовление одного изделия в период от х₁ до х₂ изделий, вычисляется по теореме о среднем

,

т.е.

.                              (4)

Заметим, что функция изменения затрат времени на изготовление изделий   часто имеет вид  , где а - затраты времени на первое изделие, b - показатель производственного процесса.

 

Пример 3. Найти среднее время, затраченное на освоение одного изделия в период освоения от х₁ = 100 до х₂ = 121 изделий, полагая в формуле

а = 600 (мин), b=0,5.

Решение. Используя формулу

,

получим

.
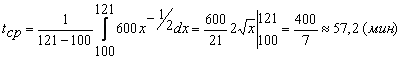