4.8. Пример решения задачи о замене оборудования

Решить задачу о замене оборудования, если =5,=10,, а разностьзадана таблично:

	0	1	2	3	4
	10	8	8	6	2

Этап . Условная оптимизация (движение от конца к началу).

С помощью уравнений Беллмана вычисляем последовательно для всех допустимых состояний:

; ;;;.

Уравнение Беллмана для шага $k=5$ имеет вид:

Поскольку начальное состояние 5-го шага есть возраст оборудования в начале 5-го шага, томожет принимать значения 0, 1, 2, 3, 4. Тогда

, ;

, ;

, ;

, ;

, .

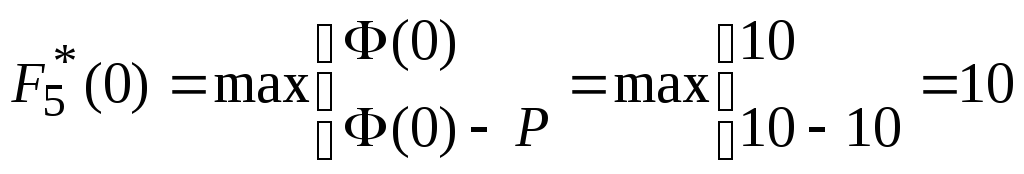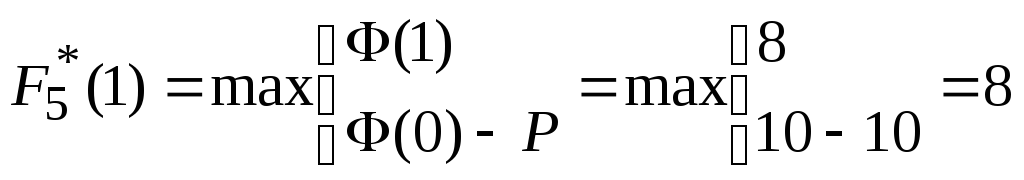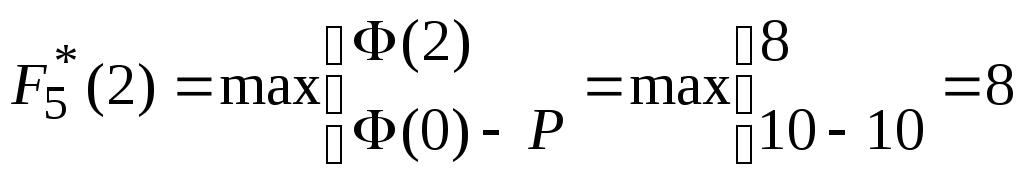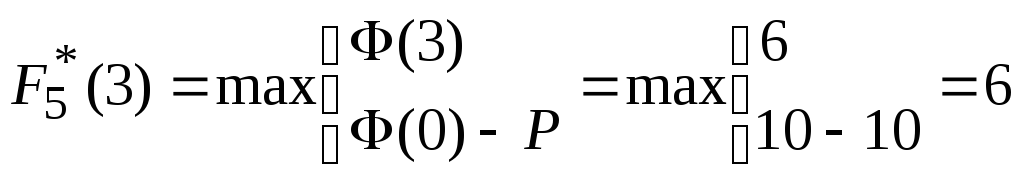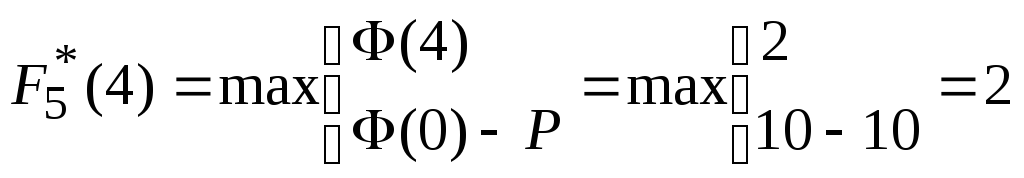Вычисление для=4, 3, 2, 1 усложняются тем, что необходимо учитывать значения, полученные на предыдущих шагах. Запишем эти вычисления для шага= 4.

Уравнение Беллмана имеет вид:

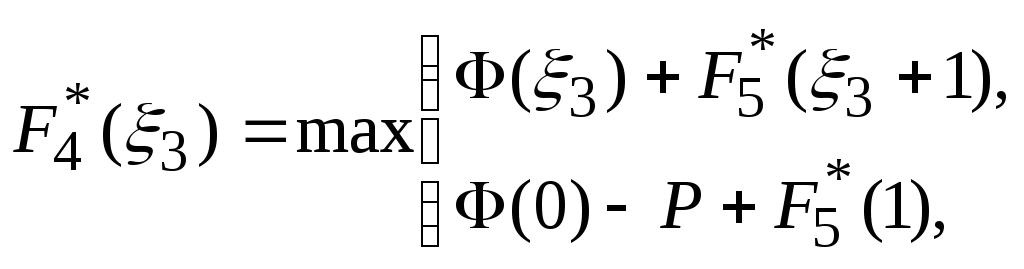
Возраст оборудования в начале 4-го шага может принимать значения 0, 1, 2, 3, 4. Тогда

, ;

, ;

, ;

, ;

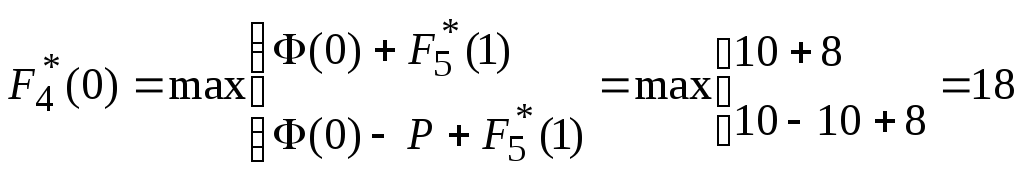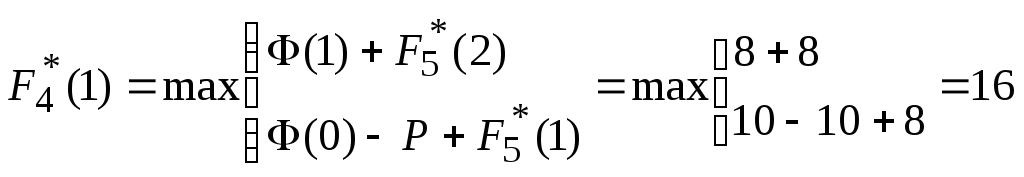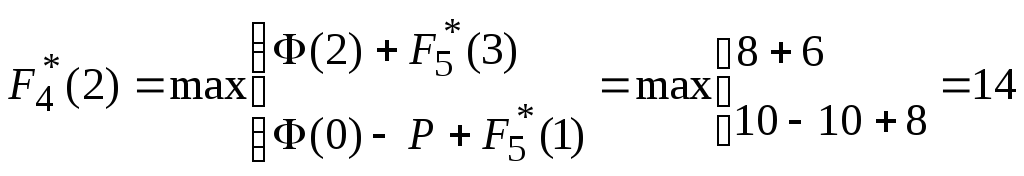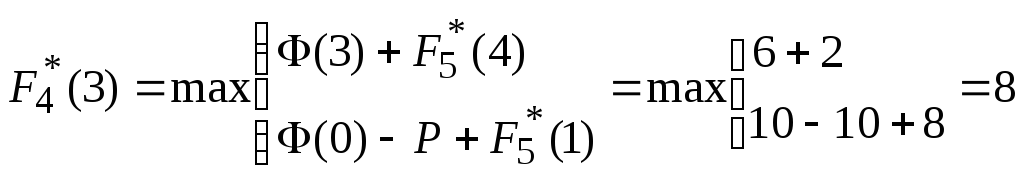и т. д. Заметим, что для случая выражение, соответствующее, принимает постоянное значение для фиксированного. Вычисления оформляем в общую таблицу:

0	10	18	26	32	34
1	8	16	22	24
2	8	14	16
3	6	8
4	2

Этап . Безусловная оптимизация (движение от начала к концу).

Используя уравнения состояний, восстанавливаем безусловное оптимальное управление:

.

Как видно из таблицы, для состояния условное оптимальное управление имеет два значенияи. Сначала рассмотрим случай:

.

Получено оптимальное управление . В случаесостояние. Этому состоянию также соответствуют два значения условного оптимального управления. Рассмотрим оба случая:

1. ,

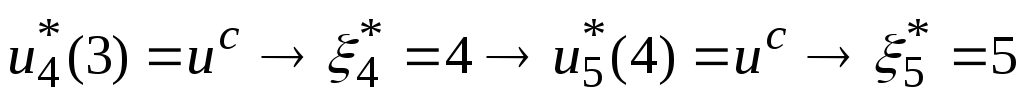получено оптимальное управление ;

2. ,

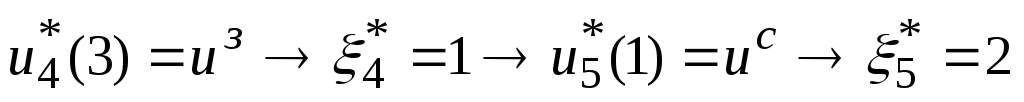получено оптимальное управление .

Восстановление оптимальных управлений дает три оптимальных варианта эксплуатации оборудования в течение 5 лет:

,,.

Из последней колонки таблицы получаем значение максимальной прибыли от эксплуатации оборудования в течение 5 лет , если начинаем эксплуатировать новое оборудование.

5.9. Задания для самостоятельной работы

5.9.1. Решить задачу распределения ресурсов по следующим данным:

1) = 40 мл н.руб.;

2) = 3;

3) средства выделяются только в размерах, кратных 10 млн. руб.;

4) функции дохода заданы таблично:

		10	20	30	40					10	20	30	40
1		4	5	7	8	12		2		4	6	8	10	13
		3	3	4	6					3	3	5	8
		4	4	5	6					4	4	5	6
3		3	5	6	7	12		4		5	7	9	10	14
		3	3	4	7					3	3	6	9
		4	4	5	5					4	4	5	7
5		3	5	7	9	12		6		4	7	10	10	14
		3	3	4	8					3	3	7	11
		4	4	5	7					4	4	5	6
7		5	5	6	9	12		8		5	8	11	11	15
		3	3	5	5					2	3	8	9
		4	4	5	5					4	4	5	8
9		6	6	8	9	13		10		6	7	11	12	15
		3	3	6	7					3	3	8	12
		4	4	5	5					4	4	5	5
11		4	4	5	6	13		12		3	4	5	6	11
		3	6	9	9					3	3	6	10
		3	3	5	7					4	4	5	6

4.9.2. Решить задачу о замене оборудования в течение 9 лет, если начальная стоимость оборудования , ликвидная стоимость, а разность между прибылью от производимой продукции и ежегодными затратами на эксплуатациюзадана таблично:

		0	1	2	3	4	5	6	7	8
1		10	8	6	4	2	1	0	0	0	52
2		10	9	8	6	4	4	2	2	0	56
3		10	9	7	7	5	3	2	1	0	61
4		10	7	7	4	4	1	1	0	0	46
5		10	8	8	6	5	4	3	2	1	59
6		10	9	8	7	6	5	4	0	0	58
7		10	9	7	7	6	6	3	3	0	56
8		10	9	8	6	4	4	3	3	0	56
9		10	9	8	7	6	6	5	5	0	58
10		10	8	8	6	5	5	4	3	2	59
11		10	8	6	5	3	2	1	0	0	47
12		10	8	6	6	5	4	1	1	0	50