11.2.2 Изменение агрегатного состояния

В разделе 11.2.2 рассматривался процесс парообразования, осуществляемый при постоянном давлении. Аналогичный переход из твердого состояния в газообразное называют возгонкой, или сублимацией, а из твердого состояния к жидкому – плавлением.

Состояния вещества при этих превращениях считают устойчивыми, стабильными. При этом всякие изменения состояния считаются квазистатическими, как это обычно принято в термодинамике.

П ереход из одного агрегатного состояния в другое удобно рассматривать на р - t – диаграмме (рисунок 11.6). Кривая АК представляет собой зависимость между давлением насыщенного пара и температурой кипения, т. е. р = f (t_н) (кривая упругости пара).

Рисунок 11.6 – р – t - диаграмма, для рассмотрения перехода из одного агрегатного состояния в другое

Кривая равновесия жидкой и газообразной фазы заканчивается в критической точке К.

Если от жидкости отбирать теплоту при постоянном давлении, то при определенной температуре жидкость переходит в твердое состояние. Температура, при которой осуществляется этот переход, называется температурой затвердевания, или плавления t_пл, а количество теплоты, отбираемое в этом процессе, называется скрытой теплотой плавления. При плавлении так же, как и при парообразовании, вещество находится в двух фазах. Аналогично кривой АК можно построить кривую AD, которая однозначно определяется зависимостью р = f(t_пл).

Кривая сублимации АВ представляет собой зависимость р = f(t_c) для перехода твердого тела в газообразное. Этот переход при температуре сублимации t_c происходит вследствие подведения некоторого количества теплоты, носящего название скрытой теплоты сублимации. Точки этой кривой соответствуют двухфазной системе твердое тело – газ (например, водяной пар над поверхностью льда).

Все три кривых равновесия (парообразования, плавления и сублимации) пересекаются в некоторой характерной для каждого вещества точке. Эта точка А называется тройной точкой, а изображаемое ею состояние – фундаментальным. В этой точке находятся в термодинамическом равновесии три различные фазы вещества: твердая, жидкая и газообразная.

Тройной точке воды соответствуют следующие параметры:

давление р = 0,00610 бар, Т =273,16 К.

Рассмотрение описанных процессов показывает, что в состояниях, находящихся между кривыми АВ, АЕ и AD, тело будет находиться целиком в одной фазе: правее АВ и АК – область газообразного состояния; левее линий AD и АВ располагается область вещества в твердом состоянии; между линиями AD и АК находится область жидкости.

В состояниях на линии АК, AD и АВ вещество может существовать в двух фазах, причем на линии АК в жидкой и газообразной, на AD – твердой и жидкой; а на линии АВ вещество может быть в твердом и газообразном состояниях. Расположение и вид этих трех кривых

AK – p = f(t_н), АD – р = f(t_пл), AB – p = f(t_c)

зависят от природы вещества и устанавливаются опытным путем.

11.2.4. Параметры состояния воды и водяного пара

Вследствие незначительной сжимаемости воды можно принять, что плотность воды при 0° С и любых давлениях есть величина постоянная, ('₀ = 0,001 м³/кг). Начало отсчета внутренней энергии энтальпии и энтропии берется от 0° С и соответствующего давления насыщения р = 0,00610 бар. При этих параметрах энтальпия, энтропия, а также внутренняя энергия воды берутся условно равными нулю: s'₀ = 0, i'₀ = 0, u'₀ = 0.

В процессе подогрева воды происходит нагревание ее до температуры кипения t_н. Удельный объем воды при температуре кипения ' будет больше объема '₀. Соответствующие значения ' для воды в функции температуры и давления для состояний, лежащих или на нижней пограничной кривой, или левее ее, даются в справочной литературе.

Количество теплоты, которое нужно сообщать воде, чтобы нагреть ее от 0° С до температуры кипения в процессе р = const, называется теплотой жидкости. Это количество теплоты определяется по формуле

, (11.15)

или

(11.16)

где – средняя теплоемкость воды в интервале температур от 0° С до t_Н°С/

При низких по сравнению с Т_кр температурах можно считать = 4,1865 кДж/(кг·град).

Воспользуемся в изобарном процессе подогрева воды первым законом термодинамики, по которому

(11.17)

где u' — внутренняя энергия воды при температуре кипения.

Так как при 0° С u₀ = 0, а работа расширения жидкости

(11.18)

практически заметна только при больших значениях давления, то

(11.19)

Энтальпия воды при температуре кипения определяется по общей формуле

(11.20)

Полагая, что , получим

(11.21)

В процессе нагревания жидкости от 0° С до температуры кипения происходит увеличение ее энтропии, которое может быть найдено по формуле

(11.22)

при s'₀ = 0 и с_Рв = 4,1865 кДж/(кг·град)

(11.23)

В процессе парообразования жидкость, нагретая до температуры кипения при этой температуре и определенном постоянном давлении, обращается в пар. Количество теплоты, затрачиваемое в процессе при р = const на превращение 1 кг воды при температуре кипения в сухой насыщенный пар той же температуры, обозначим через r.

Теплота r называется скрытой теплотой парообразования. По первому закону термодинамики

(11.24)

где u — внутренняя энергия сухого насыщенного пара;

l" — работа расширения в процессе парообразования.

Разность внутренних энергий u" – u затрачиваемая на работу против внутренних сил, называется внутренней теплотой парообразования и обозначается буквой . Теплота, затрачиваемая на работу против внешних сил, равна

(11.25)

и называется внешней теплотой парообразования. Обозначим ее буквой .

Таким образом,

(11.26)

Вследствие того, что процесс парообразования идет при постоянном давлении,

(11.27)

Величины r и i" даются в таблицах насыщенного пара, а - легко определяются по приведенным выше формулам.

С возрастанием давления, как видно из рисунка 11.7, увеличивается энтальпия жидкости и достигает максимального значения при критическом давлении. Скрытая теплота парообразования уменьшается с ростом давления и равна нулю при критическом давлении (и температуре), потому что в этих условиях различия между жидкостью и ее паром исчезают и процесс парообразования как таковой отсутствует.

Изменение энтропии в процессе парообразования при подведении к кипящей воде r кДж/кг теплоты равно

(11.28)

откуда

(11.29)

или, используя значение s из выражения (11.23),

(11.30)

Рисунок 11.7 – i - p–диаграмма воды

При полном испарении жидкости состояние сухого насыщенного пара определяется одним параметром: давлением или температурой. Поэтому объем, внутренняя энергия и энтальпия определяются по таблицам насыщенного пара по давлению или температуре.

Связь между удельными объемами жидкости и пара на линии насыщения  и  давлением насыщенного пара р_Н температурой Т_Н и скрытой теплотой парообразования может быть получена следующим образом. При превращении жидкости в пар давление насыщенного пара от объема системы не зависит, следовательно, в выражении , но так как равновесное превращение жидкости в пар происходит при постоянной температуре (Т_Н=const), то

,

где dV представляет изменение объема системы при переходе жидкости в пар. Таким образом,

(11.31)

Изменение объема системы, если испарилась жидкость массой dm, равно

,

а приращение энтропии в квазистатическом процессе испарения жидкости массой dm по (11.28)

.

Подставив эти значения в уравнение (11.31), получим

, (11.32)

где — производная от давления по температуре на кривой фазового равновесия р_Н = f (T_Н).

Уравнение (9.32) называют уравнением Клапейрона – Клаузиуса и применяют при исследованиях изменений агрегатного состояния вещества из жидкого состояния в парообразное. Аналогичные уравнения можно применять и к процессам перехода вещества из твердого состояния в жидкое или газообразное.

Параметры влажного насыщенного пара при заданной величине сухости могут быть определены из следующих соотношений.

Удельный объем влажного насыщенного пара

(11.33)

Так как объем воды (1 — х) мал по сравнению с объемом пара, то при невысоких давлениях

. (11.34)

Энтальпия влажного насыщенного пара с учетом того, что на превращение в пар х кг жидкости необходимо затратить хr кДж/кг теплоты, равна

. (11.35)

Энтропия влажного насыщенного пара

. (11.36)

Свойства перегретого пара резко отличаются от свойств насыщенного пара и приближаются к свойствам газов.

Перегретый пар характеризуется тем, что его температура выше температуры парообразования Т_H при том же давлении и удельный объем его больше, чем объем сухого насыщенного пара при том же давлении.

Количество теплоты, необходимое для перевода 1 кг сухого насыщенного пара при р = const в перегретый с температурой t, называют теплотой перегрева q_п и определяют по формуле

. (11.37)

Если с_рm – средняя массовая теплоемкость перегретого пара при постоянном давлении, то

. (11.38)

Значение с_рm берется для перегретого пара по формуле .

Энтальпия перегретого пара

(11.39)

называется полной теплотой перегретого пара. По первому закону термодинамики

, (11.40)

где – работа расширения в изобарном процессе перегрева пара;

— изменение внутренней энергии в процессе перегрева.

Изменение энтропии в равновесном изобарном процессе перегрева равно

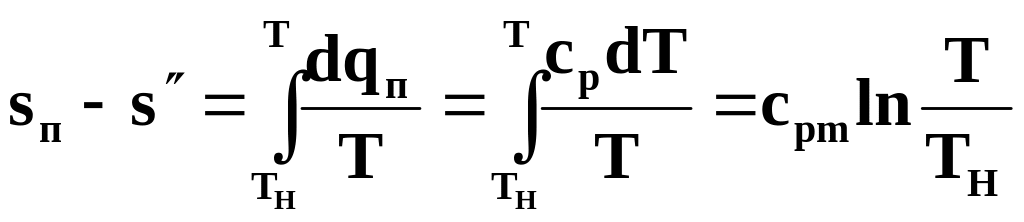(11.41)

или

. (11.42)

Свойства перегретых паров будут тем ближе к свойствам идеального газа, чем больше температура перегрева.

11.2.5 Т–s-диаграмма водяного пара

Для графического изображения процессов, происходящих в паре, удобно пользоваться Т–s - диаграммой, Площадь под кривой обратимого процесса дает количество теплоты, сообщаемое телу или отнимаемое от него. Точкам р– диаграммы соответствуют определенные точки, Т–s диаграммы (рисунок 11.8).

Рисунок 11.8 – Т–s-диаграмма водяного пара

Если было принято условно, что энтропия начального состояния воды s₀ = 0, то эта точка лежит на оси ординат на 273° выше абсолютного нуля.

Перенося по точкам нижнюю пограничную кривую (х = 0) из системы р–v в Т–s-диаграмму, получим соответствующую ей кривую, абсциссами которой являются значения s'. Аналогично наносится верхняя пограничная кривая (х=1), абсциссами которой будут значения энтропии сухого насыщенного пара s".

В точке b диаграммы начинается кипение при Т_H = const, и энтропия в процессе парообразования повышается

.

Процесс парообразования заканчивается в точке с, где

.

Так как процесс парообразования идет при Т_н = const и р – =const, изотерма b-с является одновременно и изобарой. Дальнейший подвод теплоты снова сопровождается увеличением температуры и энтропии. В процессе перегрева пара (кривая с-е)

.

Вследствие того, что площади в Т-s-диаграмме изображают количество подведенной (отведенной) теплоты, то пл. аbАО – теплота в процессе нагрева жидкости от 0° С до температуры кипения; пл. abСВ – теплота, подводимая к воде в процессе парообразования; пл. сеСВ – теплота, затраченная на перегрев пара.

Учитывая, что количество теплоты в процессе р = const равно разности энтальпий , площадь, ограниченная ординатами, осью абсцисс и изобарой, проходящей через точку, определяет энтальпию в данной точке. Точка пересечения верхней и нижней пограничных кривых является критической точкой К. Область, лежащая между кривыми аК и сK, это область влажного насыщенного пара. Область, лежащая правее верхней пограничной кривой, – область перегретого пара.

11.2.6 i–s-диаграмма водяного пара

Для изучения и расчетов различных термодинамических процессов, в которых рабочим телом является насыщенный и перегретый пар, удобна i–s-диаграмма (рисунок 11.9).

Рисунок 11.9 – i–s-диаграмма водяного пара

В системе координат i–s наносятся пограничные кривые, изобары и изотермы. Нижняя пограничная кривая и верхняя пограничная кривая строятся по известным значениям , , , и сливаются в критической точке К. В области влажного насыщенного пара наносятся линии постоянной сухости (пунктирные кривые). В этой диаграмме теплоты жидкостей, парообразование и перегрев изображаются линейными отрезками, а не площадями. Теплота парообразования по данной изобаре

равна разности ординат точек пересечения изобары с правой и левой пограничными кривыми.

Для процесса парообразования, происходящего при р = const,

, то есть .

Следовательно, в области влажного насыщенного пара изобары, являясь одновременно и изотермами, представляют собой прямые линии с угловым коэффициентом, равным T_н.

Изобары пересекают пограничные кривые без излома. Изобары и изохоры в области перегрева – слабо вогнутые логарифмические кривые. Изотермы в области перегретого пара – выпуклые кривые, поднимающиеся слева вверх направо. Чем больше температура, тем выше располагается изотерма. Чем дальше от пограничной кривой (х = 1) проходит изотерма, тем больше она приближается к горизонтали i = const, так как в области идеального газа энтальпия однозначно определяется температурой.

На рисунке 11.9 точки A, В, С изображают соответственно состояния влажного, сухого и перегретого пара. Точка А лежит на пересечении изобары (изотермы) и линии постоянной сухости. Точка В лежит на пересечении изобары и верхней пограничной кривой. Точка С находится на пересечении изобары и изотермы. По положению точки, соответствующей некоторому состоянию пара, можно определить на i–s-диаграмме числовые значения всех параметров в этой точке.