11. Реальные газы и пары

11.1 Уравнения состояния реальных газов

Все реальные газы являются парами тех или иных жидкостей. Чем ближе газ к переходу в жидкое состояние, тем больше его отклонение от свойств идеального газа, состояние которого описывается уравнением Клапейрона.

Если сжимать газ при постоянной температуре, то можно достигнуть состояния насыщения (сжижения газа), соответствующего этой температуре и некоторому определенному давлению. При дальнейшем сжатии пар будет конденсироваться и в определенный момент полностью превратится в жидкость.

Процесс перехода пара в жидкость проходит при постоянных температуре и давлении, так как давление насыщенного пара однозначно определяется температурой. На р -  –диаграмме (рисунок 11.1) область двухфазных состояний (пар и жидкость) лежит между кривыми кипящей жидкости и сухого насыщенного пара. При увеличении давления эти кривые сближаются. Сближение происходит потому, что объем пара, уменьшается, а объем жидкости увеличивается.

При некотором определенном для данной жидкости (пара) давлении кривые кипящей жидкости и пара встречаются в критической точке, которой соответствуют критические параметры: давление р_кр, температура Т_кр, удельный объем _кр, характеризующие критическое состояние вещества.

При критическом состоянии исчезают различия между жидкостью и паром. Оно является предельным физическим состоянием, как для однородного, так и для распавшегося на две фазы вещества.

При температуре более высокой, чем критическая, газ ни при каком давлении не может сконденсироваться, т. е. превратиться в жидкость.

В общем случае все газы в области, близкой к состоянию сжижения, приближенно воспроизводят связь между параметрами состояния по уравнению Клапейрона. Во всех газах с более или менее значительной плотностью нельзя пренебрегать силами сцепления между молекулами, объемом, занимаемым ими, а также ассоциацией молекул в группы.

П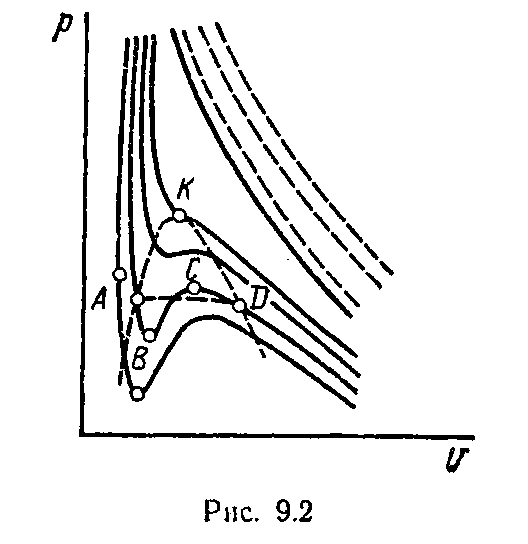 од ассоциацией понимается механическое соединение двух или нескольких молекул в одну сложную. Уменьшение числа самостоятельных частиц, из которых состоит газ, должно привести к возрастанию среднего молекулярного веса газа и уменьшению его давления. Ассоциация значительно усложняет математическое описание состояния реальных газов.

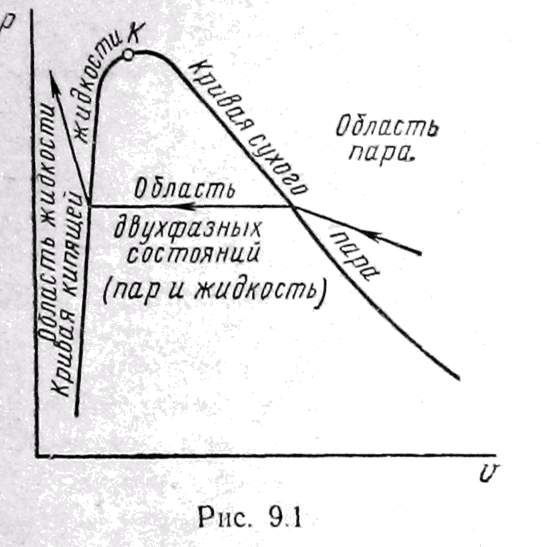
Рисунок 11.2

Рисунок 11.1 – Область двухфазных состояний (пар и жидкость)

П

Рисунок 11.1

ри уменьшении давления и возрастании температуры газа можно пользоваться уравнением состояния идеального газа за иск точением тех случаев, когда в газе под влиянием больших температур наступает изменение химической структуры (например, распад сложных молекул — диссоциация).

Уравнение состояния реальных газов выводится или чисто теоретически на основе гипотетических представлений о структуре газа, или на основании обработки экспериментальных зависимостей между р, , Т.

Широкое распространение в научных исследованиях получило уравнение Ван-дер-Ваальса, выведенное путем пересмотра некоторых допущений, лежащих в основе уравнения состояния идеального газа. Уравнение состояния реального газа с учетом сил, действующих между молекулами, и их объема для 1 кг газа имеет вид

(11.1)

Это уравнение отличается от уравнения Клапейрона двумя поправками: поправкой на объем самих молекул b и поправкой на так внутреннее давление - определяемое взаимным притяжением молекул газа. Это давление может рассматриваться как сила, действующая со стороны внешних периферийных молекул и направленная внутрь сосуда.

Рассмотрим изменения на изотермах, обусловленных поправками а и b. При температуре выше критической изотермы, построенные по уравнению Ван-дер-Ваальса, представляют собой плавные кривые, отличные от равнобоких гипербол, которые бы дало уравнение состояния идеального газа. Последние в верхней части рисунка 11.2 показаны пунктиром.

При температуре ниже критической имеется область объемов, где поправка (уменьшающая давление) играет определяющую роль и давление проходит через максимум в точке С. Для меньших объемов давление падает, проходит через минимум – точка В, а затем резко увеличивается, когда  стремится к значению b.

При критической температуре, максимум и минимум на изотермах сливаются в точке перегиба К, а так как касательная к изотерме в критической точке идет горизонтально, то для критической точки должны выполняться условия

, . (11.2)

Отсюда получаем уравнения

, (11.3)

. (11.4)

Температуру Т_кр и объем _кр можно определить из уравнений (11.3) и (11.4), а давление р_кр находится затем из уравнения (11.1). В результате получаем

, , (11.5)

Из последних соотношений можно определить индивидуальные константы а и b, зависящие от физических свойств данного газа

, . (11.6)

Так как процесс перехода от жидкого состояния к газообразному идет при постоянных Т и р, то на рисунке 11.2 этому процессу соответствует линия АD.

Однако участки АВ и СD на изотермах можно воспроизвести экспериментально только при использовании очень чистых жидкостей и газов. Вещество на этих участках находится в виде перегретой жидкости и перенасыщенного (переохлажденного) пара. Такие состояния, когда вещество остается в однофазном состоянии и не распадается на фазы, называются метастабильными.

Главная ценность уравнения Ван-дер-Ваальса состоит в том, что оно качественно правильно описывает непрерывность перехода из жидкого состояния в газообразное.

Предпринимались попытки усовершенствования его за счет того, что коэффициенты а и b принимались не постоянными, а зависящими от температуры и объема. Но эти попытки не привели к созданию уравнения состояния, описывающего свойства газа в широком диапазоне изменения параметров.

Неудачи создания общего уравнения состояния привели к появлению целого ряда эмпирических уравнений, которые могли бы с достаточной точностью предсказывать поведение реальных газов в широком диапазоне условий. Наиболее известны из них: уравнение Битти – Бриджмена с пятью эмпирически определяемыми постоянными и уравнение Бенедикта-Вебб-Рубина, содержащее восемь эмпирических постоянных – (а, b, с, d, А₀, В₀, С₀ и т.д.)

Уравнение Битти – Бриджмена, применяемое до давлений порядка 250 бар и плотностей газа, не превышающих 0,5 плотности в критической точке, имеет вид

, (11.7)

а уравнение состояния Бенедикта – Вебб – Рубина имеет вид

(11.8)

Эти уравнения могут предсказать р, , Т – свойства газа с ошибкой в пределах нескольких десятых процента.

Хорошо согласуется с опытными данными одно из современных уравнений состояния газа — уравнение Вукаловича — Новикова, учитывающее ассоциацию молекул. При учете столкновений двойных молекул это уравнение имеет вид

, (11.9)

где ,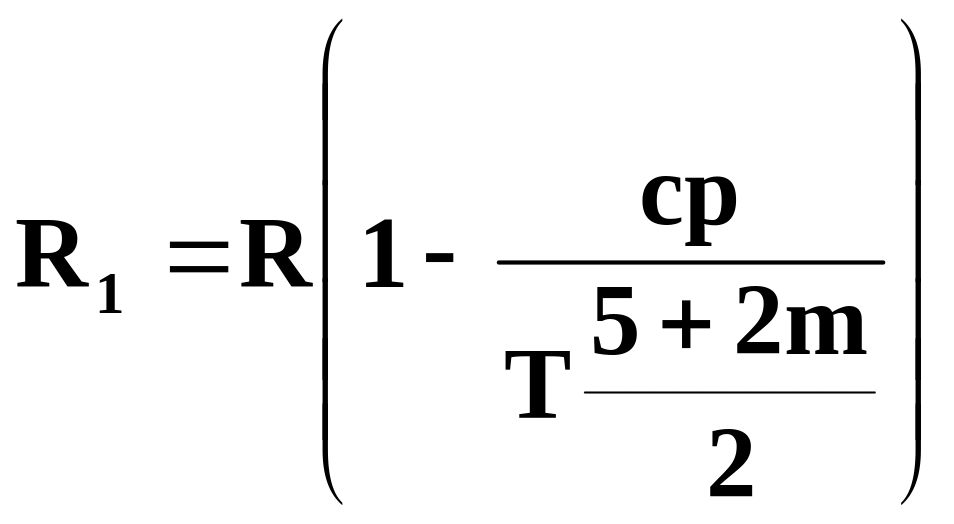

с и m — опытные константы.

В настоящее время теоретически обосновано уравнение состояния, представляющее собой разложение коэффициента сжимаемости z в бесконечный ряд по степеням 1/

, (11.10)

где В, С и D — второй, третий и четвертый вириальные коэффициенты, учитывающие взаимодействие соответственно двух трех, четырех и т. д. молекул. Вириальные коэффициенты зависят лишь от температуры и определяются, если известна зависимость потенциальной энергии взаимодействия молекул U от расстояния между ними (рисунок 11.3).

Вместо точных аналитических зависимостей U_пот= f(r) практически применяют приближенные выражения, которые называются потенциалами. Широко используется потенциал Леннарда - Джонса, по которому энергия отталкивания пропорциональна двенадцатой степени расстояния между молекулами, а энергия притяжения – шестой

, (11.11)

где r - расстояние между молекулами; — значение r, при котором U_пот = 0;  – максимальная величина энергии притяжения (глубина потенциальной ямы).

Рисунок 11.3 – Зависимость потенциальной энергии взаимодействия молекул U от расстояния между ними

Значения  и  для каждого газа могут быть определены по экспериментальным данным. Кроме потенциала Леннарда – Джонса применяются другие потенциалы, которые могут быть использованы, для определенных групп сходственных веществ.

При решении целого ряда технических задач рабочими телами могут быть не широко используемые в технике вещества (водяной пар, углекислый газ, азот и некоторые другие), а вещества, термические свойства которых неизвестны. В этом случае можно воспользоваться для предсказания свойств малоизученных веществ положением о термодинамическом подобии веществ.

Если значения индивидуальных констант а и b подставить в уравнение (11.1), то получим уравнение Ван-дер-Ваальса в функции приведенных параметров

, (11.12)

где , , .

Эти отношения называются приведенными давлением, температурой и объемом. Уравнение (10.12) можно записать в форме

(11.13)

В этой форме приведенное уравнение состояния будет одинаково для всех веществ. Состояния двух или нескольких веществ, в которых они имеют одинаковые приведенные параметры , называются соответственными состояниями, т. е. эти вещества находятся в состояниях, пропорционально удаленных от своего критического состояния.

Если вещества подчиняются одному и тому же приведенному уравнению состояния и имеют два одинаковых приведенных параметра, то у них одинаков и третий приведенный параметр, т. е. вещества, будут находиться в соответственных состояниях. Это положение носит название закона соответственных состояний.

Вещества, подчиняющиеся закону соответственных состояний, называют термодинамически подобными. Практически закон соответственных состояний наиболее удобно применять в виде зависимости , причем для расчетов можно применить – диаграмму Эта диаграмма строится по экспериментальным данным для различных веществ и может быть использована для расчета термодинамических свойств малоизученных веществ методом термодинамического подобия.

Для этого, зная критические параметры вещества, находят и , а по – диаграмме определяется коэффициент сжимаемости при данных приведенных параметрах. Значение удельного объема можно вычислить по формуле

.

Точность расчета по этому методу не превышает 15%, так как закон соответственных состояний выполняется лишь приближенно.