4.Расчётная часть

Математическая форма записи задачи выглядит следующим образом:

Рассмотрим конкретный пример:

Решение

После того, как задача выписана в специальной форме, можно записать симплекс-таблицу.

	b
L	0	7	8	3
	7	4	5	3
	1	1	0	0
	1	0	1	0
	1	0	0	1

Решаем ее симплекс методом:

	b
L	-7	-7	8	3
	3	-4	5	3
	1	1	0	0
	1	0	1	0
	1	0	0	1

	b
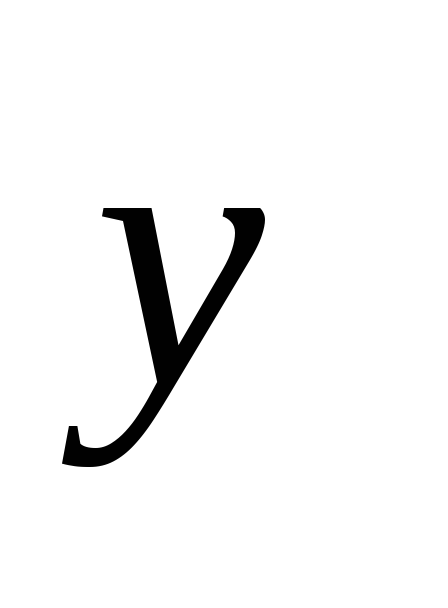
L	-59/5	-3/5	-8/5	-9/5
	3/5	-4/5	1/5	3/5
	1	1	0	0
	2/5	4/5	-1/5	-3/5
	1	0	0	1

Таблица оптимальна, но не целочисленная, решаем задачу методом Гомори. Строим отсечение по строке 1, и решаем двойственным симплекс методом.

b L -59/5 -3/5 -8/5 -9/5 3/5 -4/5 1/5 3/5 1 1 0 0 2/5 4/5 -1/5 -3/5 1 0 0 1 -3/5 -1/5 -1/5 -3/5

b L -10 0 -1 -3 0 -1 0 1 1 1 0 0 1 1 0 -1 0 -1/3 -1/3 5/3 1 1/3 1/3 -5/3

Т. к. все базисные переменные положительны и целочисленные, то симплекс-таблица оптимальна.

Отсюда следует, что максимальная прибыль равна 10 рублей, и средства выделены на первый и третий объект.

Для решения задач целочисленного линейного программирования, мною была написана программа, реализующая алгоритм метода отсечений Гомори.

5.Алгоритм программы

Список использованных источников

1. Дегтярев Ю.И. Исследование операций. - М.: Высшая школа, 1986. – 224с.

2. Зайченко Ю.П. Исследование операций. - Киев: Высшая школа, 1979.

3. Методика по математическому программированию в электронном виде.