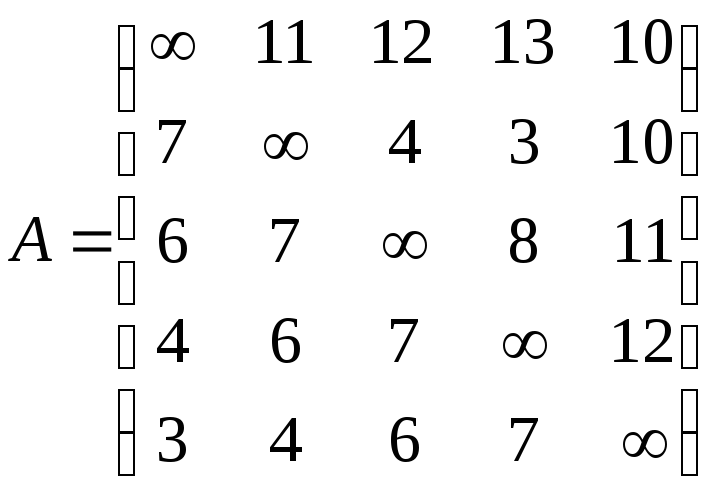
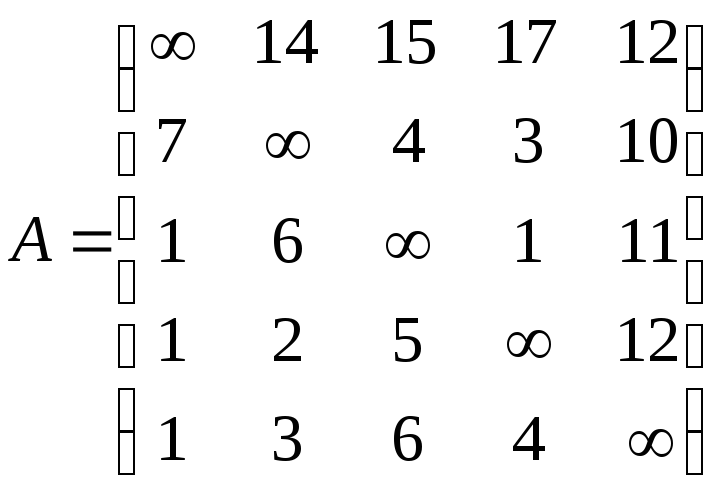
3.6 Задания по задаче о коммивояжере

3.1			3.2
3.3			3.4
3.5			3.6
3.7			3.8
3.9			3.10
3.11			3.12
3.13			3.14
3.15			3.16
3.17			3.18
3.19			3.20
3.21			3.22
3.23			3.24

4. Динамическое программирование

Методом динамического программирования (ДП) решаются задачи математического программирования, удовлетворяющие принципу последовательной оптимизации: решение исходной задачи оптимизации большой размерности заменяется решением последовательности задач оптимизации малой размерности. В силу этого основным условием применимости метода ДП является возможность разбиения процесса принятия решений на ряд однотипных шагов, или этапов, каждый из которых планируется отдельно, но с учетом результатов, полученных на других шагах.

Рассмотрим, как происходит разбиение процесса принятия решений (который мы будем представлять как процесс функционирования некоторой системы) на nшагов. Обозначим черезначальное состояние всего процесса, в то же времябудет начальным состоянием первого шага. Тогда– состояние системы после первого шага (или начальное состояние второго шага),– состояние системы после второго шага (или начальное состояние третьего шага) и т.д.

Переход от начального состоянияk-го шагакконечному состояниюk-го шагапроисходит так.

Имеется набор допустимых управлений(способов действия на шагеk), каждое из которых позволяет перейти из состоянияк одному из возможных конечных состоянийk-го шага. Выбраное наk-м шаге управление обозначим через, а состояние, в которое перейдет процесс из состоянияпод воздействием управления, обозначим. При этом предполагается, что состояниезависит оти, и не зависит от того, каким образом процесс перешел в состояние(принцип отсутствия последействия). Это предположение записывается в виде уравнений состояний

, .

С учетом введенных понятий состояний и управлений запишем показатели эффективности для всего многошагового процесса и для каждого k-го шага процесса. Предполагая, что показатель эффективностиk-го шага зависит от начального состояния на этом шагеи от управления на этом шаге, получаем целевую функцию наk-м шаге в видеи целевую функцию всего многошагового процесса в виде

.

Сформулируем теперь задачу ДП. Определить совокупность допустимых управлений , переводящих процесс из начального состоянияв конечное состояниеи максимизирующих или минимизирующих показатель эффективности.

Управление, при котором достигается максимум (минимум) целевой функции F, называетсяоптимальным управлением.

Основное правило ДП, сформулированное американским математиком Р. Беллманом, называется принципом оптимальности: оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет процесс в конце данного шага.