3.2.Двойственный симплекс-метод

Метод работает с теми же симплексными таблицами, что и прямой симплекс - метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис.

Вычислительная схема двойственного симплекс – метода

Шаг 0. Начинаем с симплексной таблицы

	B		…
L			…
			…
…	…	…………..
			…

где .

Шаг 1. Проверка на оптимальность. Если , то решение- оптимальное.

Шаг 2. Выбор ведущей строки. Выбираем среди номеров i, для которых , номерk с максимальным по модулю значением

Строка k объявляется ведущей.

Шаг 3. Проверка на неразрешимость. Если в строке нет отрицательных элементов, то двойственная целевая функция неограничена и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.

Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки элемент с номеромs, для которого выполняется равенство

Столбец s объявляется ведущим, а элемент -ведущим элементом.

Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).[2]

3.3.Метод Гомори

Метод Гомори для нахождения целочисленного решения относится к большой группе методов, называемых методами отсечений. Эти методы основаны на введении в задачу дополнительных ограничений, позволяющих учесть требование целочисленности. Основная идея методов отсечений состоит в том, что на полученное оптимальное нецелочисленное решение накладывается дополнительное ограничение, которое делает это решение недопустимым, но и не отсекает ни одного целочисленного решения от области допустимых решений.

3.3.1.Методы отсечения и их сущность

Рассмотрим общую задачу целочисленного программирования в постановке:

_., назовем эту задачу — задачей.

Задача без учета целочисленности:

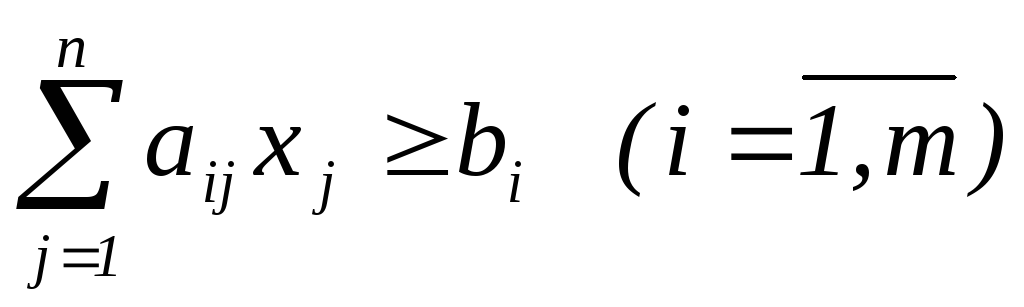
_, назовем — -задачей.

Теорема:

Пусть G- многогранник, -множество его целых точек, R- выпуклая линейная оболочка множества , тогда:

1) -целочисленный многогранник;

2) ;

3) - множество опорных планов задачисодержится в

.

3.3.2.Общий алгоритм метода Гомори

Определение.

Правильное отсечение - отсечение, которое удовлетворяют следующим требованиям:

1. линейно;

2. отсекает часть области, не содержащей допустимых решений целочисленной задачи

3. не отсекает ни одного целочисленного оптимального плана.

Этапы решения:

1. Решается -задача, соответствующая исходнойзадаче.

Если -задача не имеет решения, т.е. G пуста или неограниченна в положительном направлении возрастания (убывания) F, то устанавливается неразрешимость целочисленной задачи.

2. Оптимальное решение -задачи проверяется на целочисленность.

Если решение целочисленное, то задача решена.

В противном случае, если условие целочисленности не выполняется хотя бы по одной координате, то переходят к третьему этапу.

3. Дополнительное ограничение, которое

1. линейно;

2. отсекает часть области, не содержащей допустимых решений целочисленной - задачи;

3. не отсекает ни одного целочисленного оптимального плана, который входит в систему ограничений. [4].

Шаг 0.Пусть оптимальная таблица имеет вид:

	b		…
L			…
			…
…	…	…………..
/			…

Среди элементов – есть дробные числа.

Шаг 1. Среди дробных компонент таблицы выбираем элементс максимальной дробной частьюи по строкеi составляем дополнительное ограничение:

Здесь - целая часть числа(наибольшее целое число, не превышающее число).

Шаг 2. Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.

Замечания.

• Признаком отсутствия целочисленного решения служит появление в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами.

• На шаге 2 двойственный симплекс-метод применяется до тех пор, пока не будет получена оптимальная симплексная таблица (возможно потребуется несколько итераций).

• Если на шаге 2 в базис вводится переменная дополнительного ограничения , то эта строка вычеркивается из симплексной таблицы (соответствующее ограничение является избыточным).