
- •Содержание
- •Раздел 1 Дифференциальное исчисление функций нескольких переменных
- •1.1 Нахождение области определения и вычисление пределов для функции нескольких переменных
- •1.3 Нахождение области определения и вычисление пределов для функции нескольких переменных
- •Раздел 2 Интегральное исчисление функций нескольких переменных
- •2.1 Вычисление двойного интеграла в случае области 1 и 2го типа. Решение задач на приложения двойных интегралов
- •Раздел 3 Основы теории рядов
- •3.1 Исследование сходимости знакоположительных рядов
- •3.3 Исследование сходимости знакочередующихся рядов
- •3.5 Нахождение радиуса и области сходимости степенного ряда
- •3.7 Разложение элементарных функций в ряд Тейлора. Применение степенных рядов
- •Раздел 4 Численные методы
- •4.1 Вычисление погрешностей результатов арифметических действий
- •4.3 Решение алгебраических уравнений приближенными методами
- •4.5 Составление интерполяционных формул Лагранжа и Ньютона
- •4.7 Вопросы к экзамену
- •Раздел 1. Дифференциальное исчисление функций нескольких переменных.
- •Раздел 2. Интегральное исчисление функций нескольких переменных.
- •Раздел 3. Основы теории рядов.
- •Раздел 4. Численные методы.
- •Список использованных источников
- •Приложение а
- •Приложение б
Раздел 4 Численные методы
4.1 Вычисление погрешностей результатов арифметических действий
Пусть
 - приближение величины, точное значение
которой равно
- приближение величины, точное значение
которой равно
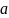 .
.
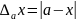 (29)
(29)
- абсолютная погрешность приближения.
 0)
0)
- относительная погрешность приближения.
 (31)
(31)
- граница относительной погрешности,
где
 - граница абсолютной погрешности.
- граница абсолютной погрешности.
Рассмотрим типовые задания с подробными решениями и указаниями или методические рекомендации к выполнению задания.
Пример 1. Известно, что
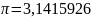 .
Найти абсолютную и относительную
погрешность приближения
.
Найти абсолютную и относительную
погрешность приближения
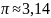 .
.
Решение: Пусть

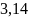 -
приближение величины, точное значение
которой равно
-
приближение величины, точное значение
которой равно
 .
.
Тогда
 =0,0015926
- абсолютная погрешность приближения.
=0,0015926
- абсолютная погрешность приближения. - относительная погрешность приближения.
- относительная погрешность приближения.
Пример 2. При измерении длины
 и диаметра
и диаметра
 некоторого провода получены значения
некоторого провода получены значения
 м,
м,
 мм. Вычислить границы относительных
погрешностей
мм. Вычислить границы относительных
погрешностей
 и
и
 .
.
Решение:
 и
и
 .
В процентах получим:
.
В процентах получим:
 и
и
 .
.
Пример 3. Для приближения
 граница относительной погрешности
равна
граница относительной погрешности
равна
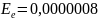 .
Найти границу абсолютной погрешности
.
Найти границу абсолютной погрешности
 .
.
Решение: из формулы
 находим
находим
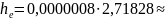
 .
.
4.3 Решение алгебраических уравнений приближенными методами
Задача о нахождении приближенных
значений действительных корней уравнения
f(x)=0
предусматривает предварительное
отделение корня, т.е. установление
промежутка в котором других корней
данного уравнения нет. Мы будем предлагать,
что функция f(x)
в промежутке [a,b]
непрерывна вместе со своими производными
f’(x) и
f’’(x),
значения f(a)
и f(b) функции
на концах промежутка имеют разные знаки,
т.е.
 ,
и обе производные сохраняют знак во
всем промежутке [a,b].
,
и обе производные сохраняют знак во
всем промежутке [a,b].
Метод хорд. Требуется вычислить действительный корень уравнения f(x)=0, изолированный на отрезке [a,b]. Пусть f(a)<0 и f(b)>0. По формуле
 ,
(32)
,
(32)
где x1 принадлежит
интервалу (a,b).
Пусть
 ,
тогда за новый интервал изоляции корня
можно принять [x1;b].
Тогда
,
тогда за новый интервал изоляции корня
можно принять [x1;b].
Тогда
 и т.д. (33)
и т.д. (33)
Последовательность чисел
 стремится к искомому корню уравнения
f(x)=0.
Вычисление приближенных значений корней
уравнения следует вести до тех пор,
которые мы хотим сохранить в ответе
(т.е. пока не будет достигнута заданная
степень точности).
стремится к искомому корню уравнения
f(x)=0.
Вычисление приближенных значений корней
уравнения следует вести до тех пор,
которые мы хотим сохранить в ответе
(т.е. пока не будет достигнута заданная
степень точности).
Метод касательных. Требуется
вычислить действительный корень
уравнения f(x)=0,
изолированный на отрезке [a,b].
Будем предполагать, что все ограничения,
сформулированные вначале относительно
f(x), сохраняют
силу и сейчас. Возьмем на [a,b]
число x0 , при котором
f(x0)
имеет тот же знак, что и f’’(x0),
т.е. такое, что
 (можно взять один из концов данного
отрезка, при соблюдении этого условия
в нем). М0(x0,f(x0))
–точка касания. Тогда
(можно взять один из концов данного
отрезка, при соблюдении этого условия
в нем). М0(x0,f(x0))
–точка касания. Тогда
 .
(34)
.
(34)
М1(x1,f(x1))
–точка касания. Тогда
 и т.д. Полученная последовательность
корней x0, x1,
x2 имеет своим
пределом искомый корень.
и т.д. Полученная последовательность
корней x0, x1,
x2 имеет своим
пределом искомый корень.
Комбинированный метод
.
 ,
,
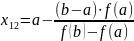 .
(35)
.
(35)
 ,
,
 и т.д. (36)
и т.д. (36)
Продолжаем вычисления до тех пор пока
не станет выполняться
 ,
где
,
где
 - достаточно малое число.
- достаточно малое число.
Рассмотрим типовые задания с подробными решениями.
Пример 1. Методом хорд и методом
касательных найти положительный корень
уравнения
 с точностью до 0,01.
с точностью до 0,01.
Решение.
Метод хорд.
Находим промежуток в котором будет
положительный корень (1; 1,7), т.к.
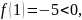
 .
.
 .
Так как
.
Так как
 ,
следовательно (1,588;1,7). Продолжаем
вычисления:
,
следовательно (1,588;1,7). Продолжаем
вычисления:
 .
Так как
.
Так как
 ,
следовательно (
,
следовательно ( ;1,7).
Продолжаем вычисления:
;1,7).
Продолжаем вычисления:
 .
Так как
.
Так как
 ,
следовательно (
,
следовательно (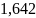 ;1,7).
Продолжаем вычисления:
;1,7).
Продолжаем вычисления:
 .
Так как
.
Так как
 ,
следовательно искомый корень с точностью
до 0,01 равен 1,64.
,
следовательно искомый корень с точностью
до 0,01 равен 1,64.
Метод касательных.
 .
Так как f(x)
и f’’(x) при
x0=1,7 имеют один и
тот же знак, а именно:
.
Так как f(x)
и f’’(x) при
x0=1,7 имеют один и
тот же знак, а именно:
 ,
то воспользуемся формулой:
,
то воспользуемся формулой:
 ,
,
 ,
,
 .
Следовательно искомый корень с точностью
до 0,01 равен 1,64.
.
Следовательно искомый корень с точностью
до 0,01 равен 1,64.
