Раздел 3 Основы теории рядов

3.1 Исследование сходимости знакоположительных рядов

Числовым рядом называется выражение вида

, (15)

где общий член ряда.

Признаки сходимости числового (знакоположительного) ряда.

1) Необходимый признак

Ряд сходится, если

, (16)

иначе ряд расходится.

2) Признак сравнения

Пусть даны два ряда с неотрицательными членами:

(17)

(18)

Если для любого n, то из сходимости ряда (17) следует сходимость ряда (18); из расходимости ряда (18) следует расходимость ряда (17).

3) Признак Даламбера

Пусть дан ряд с положительными членами. Допустим, что существует

. (19)

Тогда:

• если , то ряд сходится;

• если , то ряд расходится;

• если , то о сходимости ничего сказать нельзя, (другой признак).

4) Признак Коши

Пусть дан ряд с положительными членами. Допустим, что существует

. (20)

Тогда:

• если , то ряд сходится

• если , то ряд расходится

• если , то о сходимости ничего сказать нельзя, (другой признак).

Вспомним алгоритм раскрытия неопределенности для вычисления пределов при .

1) Найти m и n, где m – наивысшая степень числителя, n - наивысшая степень знаменателя;

2) Сравнить m и n:

• если , где и коэффициенты при и ;

• если ;

• если .

Рассмотрим типовые задания с подробными решениями.

Пример 1: Исследовать на сходимость .

Решение: используем необходимый признак . Подставим в формулу (16): . Ряд сходится.

Пример 2: Исследовать на сходимость .

Решение: используем признак Коши. 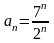. Подставим в формулу (20): . Ряд расходится.

Пример 3: Исследовать на сходимость .

Решение: используем признак Даламбера. , тогда

. Подставим в формулу (19):

. Ряд сходится.

Пример 4: Исследовать на сходимость ряд .

Решение: 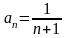. По признаку Лейбница ряд расходится, т.к.: Первое условие - выполняется. Второе условие - выполняется

3.3 Исследование сходимости знакочередующихся рядов

Числовой ряд:

(21)

называется знакопеременным рядом, если среди его членов имеются как положительные, так и отрицательные числа. Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки.

Признак Лейбница для знакочередующихся рядов.

Ряд сходится, если выполняются два условия: 1) его члены убывают по модулю; 2) общий член ряда стремится к нулю, т.е.

и (22)

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд , составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.

Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно сходящимся.

Рассмотрим типовые задания с подробными решениями.

Пример 1. Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:

Решение: Члены данного ряда по абсолютной величине монотонно убывают: . Следовательно, согласно признаку Лейбница, ряд сходится. Ряд , составленный из абсолютных величин членов данного ряда, является гармоническим рядом, который, как известно, расходится. Поэтому данный ряд сходится условно.

Пример 2. Исследовать сходимость знакопеременного ряда

Решение: Составим ряд из абсолютных величин членов данного ряда: Для исследования этого ряда применим признак Даламбера. Имеем , ,

Ряд, составленный из абсолютных величин, сходится; следовательно, данный знакопеременный ряд сходится абсолютно.