Содержание

Раздел 1 Дифференциальное исчисление функций нескольких переменных………………………..………………………………..
1.1 Нахождение области определения и вычисление пределов для функции нескольких переменных …………………………………………...
1.3 Нахождение области определения и вычисление пределов для функции нескольких переменных………………………………………..
Раздел 2 Интегральное исчисление функций нескольких переменных…………………………………………………………
2.1 Вычисление двойного интеграла в случае области 1 и 2го типа. Решение задач на приложения двойных интегралов …..………………
Раздел 3 Основы теории рядов……………………………….………………
3.1 Исследование сходимости знакоположительных рядов ……………….
3.3 Исследование сходимости знакочередующихся рядов…………………
3.5 Нахождение радиуса и области сходимости степенного ряда ………..
3.7 Разложение элементарных функций в ряд Тейлора. Применение степенных рядов………………………………………………………….
Раздел 4 Численные методы………………….………………………………
4.1 Вычисление погрешностей результатов арифметических действий….
4.3 Решение алгебраических уравнений приближенными методами……..
4.5 Составление интерполяционных формул Лагранжа и Ньютона………
4.7 Вопросы к экзамену………………………………………………………
Список использованных источников………………………..……………….
Приложение А…………………………………………………………………
Приложение Б………………………………………………………………….

Раздел 1 Дифференциальное исчисление функций нескольких переменных

1.1 Нахождение области определения и вычисление пределов для функции нескольких переменных

Переменная величина z называется функцией двух переменных величин x и y, если каждой паре допустимых значений x и y соответствует единственное значение z.

Обозначается: . Множество всех точек, в которых определена функция n переменных, называется областью определения функции. Некоторую замкнутую область D на плоскости, ограниченную данными линиями, можно задать с помощью одной или нескольких систем неравенств вида:

. (1)

Рассмотрим типовые задания с подробными решениями.

Пример 1. Найти область определения функции:

Решение:

, а 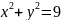- уравнение окружности с центром в точке (0,0) и R=3. Неравенству удовлетворяют координаты всех точек, которые находятся внутри окружности, а так же на самой линии окружности.

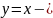
Пример 2. Область D задана параллелограммом со сторонам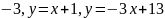и

и 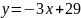. Записать с помощью систем неравенств множество точек заданной области.

Решение: Найдем точки пересечения заданных прямых и построим параллелограмм.

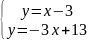, А(4;1)

, С(7;8)

, В(8;5)

, Е(3;4)

Через вершины А,Е и С на рисунке 1 проведем прямые, параллельные оси Оy. Область D, ограниченную заданным параллелограммом, разделим этими прямыми на три области D₁, D₂, D₃. Каждую из этих областей представим системой неравенств.

В области D₁ x изменяется в промежутке . Эта область ограничены снизу прямой , а сверху – прямой , т.е. . Следовательно, множество точек области D₁ можно записать в виде системы неравенств .

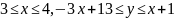В области D₂:

В области D₃:

Рисунок 1 – Решение примера 2