36) Дифференциальные уравнения движения точки.

Основное уравнение динамики

можно записать так или так

Проецируя уравнение на оси координат получаем

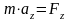
так как 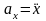, , , то

Основные задачи динамики

Первая или прямая задача:

Известна масса точки и закон ее движения, необходимо найти действующую на точку силу.

m

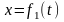
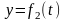
Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат

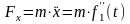
Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:

Вторая или обратная задача:

Известна масса точки и действующая на точку сила, необходимо определить закон движение этой точки.

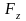
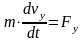
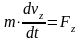
- постоянные интегрирования которые определяются исходя из начальных условий.

37) Количеством движения материальной точки 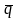называется вектор, равный произведению массы точки на ее скорость .

Количество движения точки в физике часто называют импульсом материальной точки.

Проекции количества движения точки на прямоугольные декартовы оси координат равны:

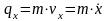
Количеством движения системы материальных точек 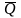называется векторная сумма количеств движений отдельных точек системы.

Количество движения системы можно выразить через массу системы и скорость центра масс.

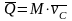
38) Меры действия сил

Элементарным импульсом силы (обозначается  ) называется векторная мера действия силы за элементарный промежуток времени  , определяемая произведением:  . 

 Импульсом силы за конечный промежуток времени    (обозначается  ) называется определенный интеграл 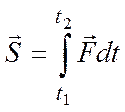   .   Если на точку действуют несколько сил,  то, пользуясь свойством определенного интеграла, можно показать, что импульс равнодействующей равен сумме импульсов составляющих сил.

Элементарной работой силы (обозначается  ) называется скалярная мера действия силы на элементарном перемещении   точки ее приложения, определяемая скалярным произведением   . 

39) Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом -  , а внутренние -  .

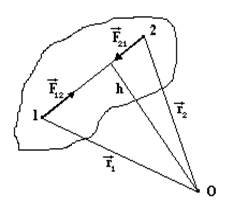Пусть система состоит из n точек. Тогда по третьему закону Ньютона, например, для точек 1 и 2,(рис.39) внутренние силы взаимодействия этих точек равны по величине и противоположны по направлению:

Равнодействующая внутренних сил состоит из векторной суммы сил действия и противодействия, которая

Рис.39 равна нулю:

Если рассмотреть сумму моментов сил  и  относительно некоторой произвольной точки О, то легко видеть, что