Абсолютное твердое тело – тело, расстояние между двумя любыми частицами которого остается неизменно.
Сила – это мера взаимодействия двух тел.
Система сил - называется группа сил, которые действуют на рассматриваемое тело или (в общем случае) на точки механической системы.
Уравновешенной системой сил - называется такая система сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.
Две системы сил называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях.
Равнодействующей
силой
рассматриваемой
системы сил называется сила, действие
которой на твердое тело или материальную
точку
эквивалентно
действию этой системы сил. Равнодействующую
силу обозначают обычно
2) Аксиомы статики
Аксиома о равновесии двух сил. Две силы равные по модулю, направленные вдоль одной прямой в разные стороны, уравновешиваются.
Аксиома о добавлении (отбрасывании) уравновешенной системы сил. Равновесие твердого тела не изменится если в системе сил действующих на него добавить или отнять уравновешивающиеся силы.
Аксиома параллелограмма сил. Равнодействующая двух сил, приложенных к одной точке, приложенную в той же точке и равную по величине и направлению диагонали параллелограмма, построенного на этих силах, как на сторонах.
Аксиома о равенстве действия и противодействия. Два тела действуют друг на друга с силами равными по модулю и противоположными по направлению.
Аксиома отвердевания. Равновесие не абсолютно твердого тела не изменяется после его затвердевания.
3
)
Свободное
тело – это
тело которое может перемещаться в любом
направлении.
Связь – это тело которое ограничивает свободу движения другого тела.
Сила с которой связь действует на рассматриваемое тело называется реакцией связи.
Силы: активные, реакции связи.
Принцип освобождения от связи: Любое несвободное тело можно рассматривать как свободное если мысленно отбросить связи и действия этих связей заменить реакциями.
Реакция связи прикладывается в точке контакта взаимодействия тел, направляется по нормали и взаимодействующим поверхностям в сторону противоположного тому направлению в котором связь препятствует к перемещению данного тела
4)Системой сходящихся сил (или пучком сил) называется такая система сил, линии действия которой пересекаются в одной точке – центре пучка.
Р
авнодействующая
системы сходящихся сил равна векторной
сумме слагаемых сил и определяется
замыкающей стороной многоугольника,
построенного на этих силах. Точка
приложения равнодействующей силы
совпадает с точкой пересечения линий
действия сил.
Проекции равнодействующей силы на оси координат равны алгебраической сумме проекций составляющих сил на эти оси.
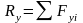
5)
Если R равнодействующая системы сходящихся сил
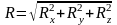
направляющие косинусы
6) Геометрическое условие для равновесия сходящейся системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая сила была равна нулю.
Аналитическое условие для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех прямоугольных осей координат были равны нулю.
,
,
,
7) Теорема о трех силах. Если твердое тело под действием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таких трех сил пресекаются в одной точке.
следовательно силы пересекаются в одной точке.
8) Система двух равных по модулю и противоположных по направлению, параллельных сил называется парой сил.
Пара сил не имеет равнодействующей и не может быть заменена уравновешивающей силой.
и
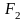- это пара сил
Плоскость в которой расположена пара сил называется плоскостью действия пары.
Кратчайшее расстояние между линиями действия сил образующих пару называется плечом пары.
Момент пары сил
– это произведение модуля одной из сил
данной пары на ее плечо.
Вращение против часовой стрелки знак «+», по часовой «-»
Вектор момента пары сил перпендикулярен плоскости действия пары и направлен таким образом чтобы глядя с его острия видеть вращение против часовой стрелки.
9) Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.
Доказательство:
Пусть на твердое тело действует пара
сил
.
Перенесем силу
в точку
,
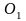а силу
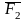в точку
.
Проведем через точки
две любые параллельные прямые,
пересекающие линии действия сил пары.
Соединим точки
отрезком прямой и разложим силы
в
точке
и
в точке
по правилу параллелограмма.
Так как
,
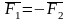то
и
П
оэтому
эквивалентна системе
,
а эта система эквивалентна системе
,
так как
эквивалентна нулю.
Таким образом мы заданную пару сил заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.
Момент исходной
пары сил
численно равен площади параллелограмма
,
а момент пары сил
численно равен площади параллелограмма
.
Но площади этих параллелограммов
равны, так как площадь треугольника
равна площади треугольника
.
Что и требовалось доказать.
Выводы:
1
,Пару
сил как жесткую фигуру можно как угодно
поворачивать и переносить в ее плоскости
действия.
2,У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.
10) Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.
Доказательство:
Пусть на твердое тело действует пара
сил
в плоскости
.
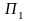Из точек приложения сил А и В опустим
перпендикуляры на плоскость
и в точках их пересечения с плоскостью
приложим две системы сил
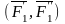и
,
каждая из которых эквивалентна нулю.
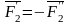
Сложим две равные
и параллельные силы
и
.
Их равнодействующая
параллельна этим силам, равна их сумме
и приложена посредине отрезка
в точке О.
Сложим две равные
и параллельные силы
и
.
Их равнодействующая
параллельна этим силам, равна их сумме
и приложена посредине отрезка
в точке О.
Так как
,
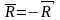то система сил
эквивалентна нулю и ее можно отбросить.
Таким образом пара сил эквивалентна паре сил , но лежит в другой, параллельной плоскости. Что и требовалось доказать.