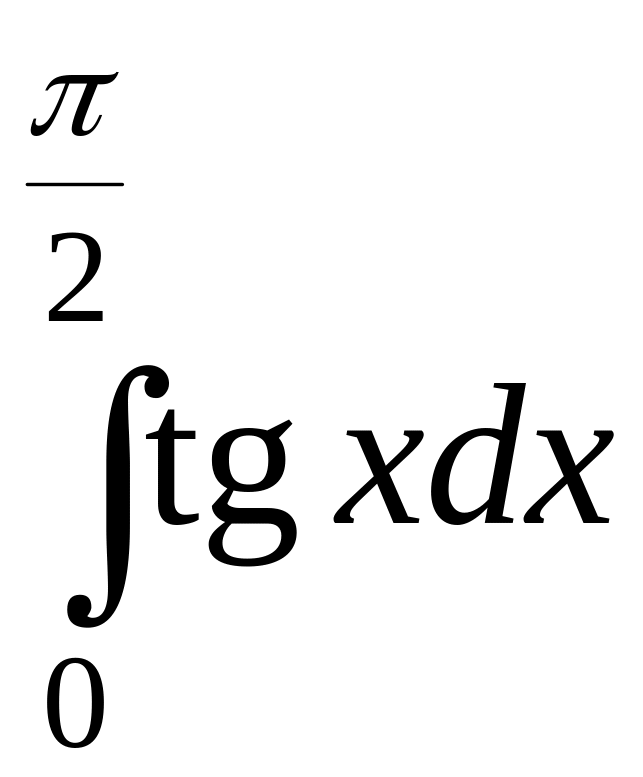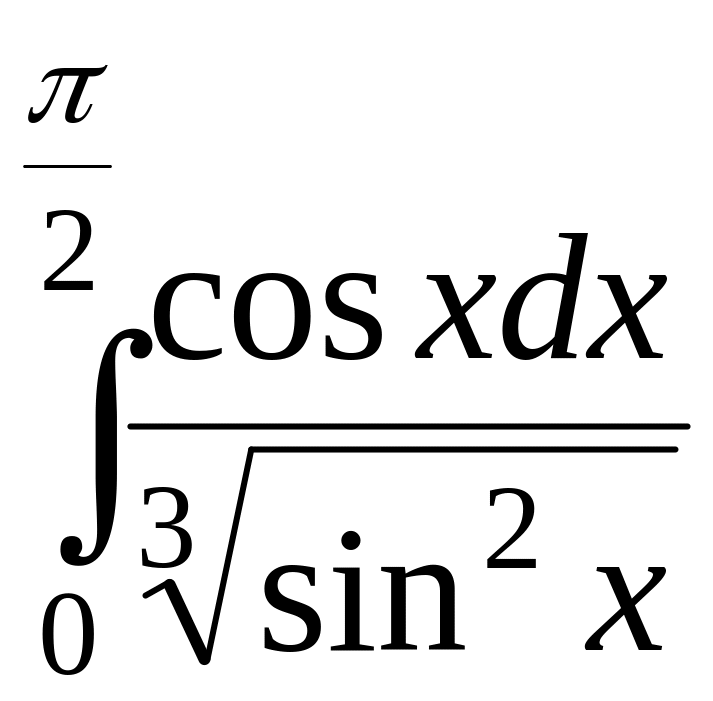- •Расчетно-графическая работа № 4 «определенный интеграл и его применение» Задание к расчетно-графической работе
- •Задание № 1.
- •Исходные данные для решения задачи
- •Исходные данные для решения задачи
- •Задание № 2.
- •Исходные данные для решения задачи
- •Задание № 3.
- •Исходные данные для решения задачи
- •Задание № 4.
- •Исходные данные для решения задачи
- •Задание № 5.
- •Исходные данные для решения задачи
- •Задание № 6.
- •Исходные данные для решения задачи
Задание № 6.
Вычислить несобственные интегралы или установить их расходимость.
Исходные данные для решения задачи
Номер варианта |
Интеграл |
Интеграл |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Решение типовых задач
Задание № 1.
Вычислить определенный интеграл .
Решение.
Выполним
замену переменной. Пусть
![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() .
Находим новые пределы интегрирования.
Если
.
Находим новые пределы интегрирования.
Если
![]() ,
то
,
то
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
что следует из зависимости
.
,
что следует из зависимости
.
Тогда
![]()
Применим
формулу интеграла от степенной функции
![]() и формулу Ньютона-Лейбница
и формулу Ньютона-Лейбница
![]() :
:
 .
.
Ответ:
![]() .
.
Вычислить определенный интеграл .
Решение.
Используем формулу интегрирования по частям:
![]() .
.
Пусть
![]() ,
,
![]() .
Находим
.
Находим
![]() ,
,
![]() .
.
Тогда
![]()
![]()

![]() .
.
Ответ:
![]() .
.
Задание № 2.
Вычислите
площадь фигуры, ограниченной линиями
![]() и
и
![]() .
Построить фигуру.
.
Построить фигуру.
Решение.
Построив линии, получим фигуру (рис. 12).

Рис. 12. Фигура
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
![]() .
.
Решим полученное квадратное уравнение:
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Вычисление площади осуществляем по формуле:
![]() ,
,
где
![]() ,
,
![]() – кривые, ограничивающие фигуру
– кривые, ограничивающие фигуру
![]() .
.
Тогда
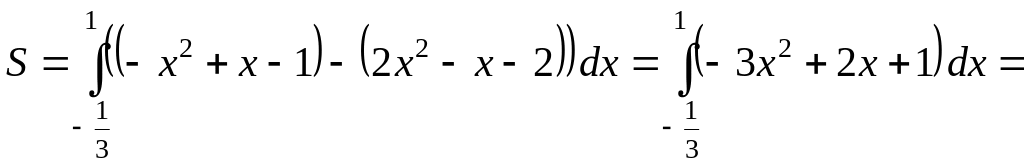
![]()
![]() (кв.
ед.).
(кв.
ед.).
Ответ:
![]() (кв. ед.).
(кв. ед.).
Задание № 3.
Найти
площадь, ограниченную линией
![]() .
.
Решение.
Заданная линия – трехлепестковая роза (рис. 13).

Рис.13. Фигура
Для вычисления площади фигуры в полярных координатах используем формулу
![]() .
.
Найдем площадь половинки одного лепестка и умножим ее на 6:

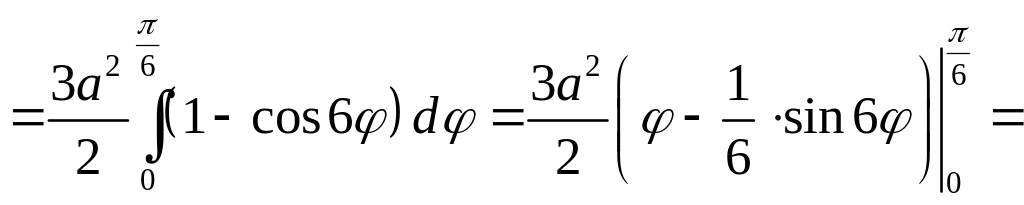
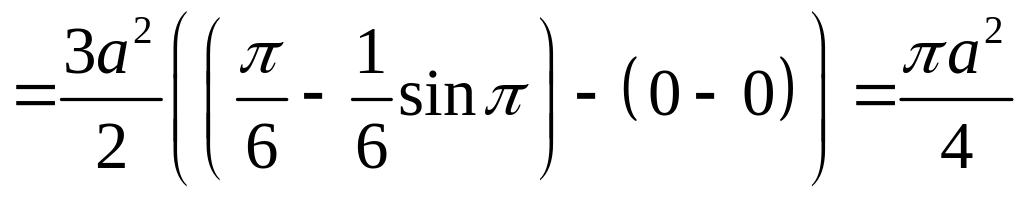 (кв.
ед.).
(кв.
ед.).
Ответ:
![]() кв. ед.
кв. ед.
Задание № 4.
Вычислить
объем тела, образованного вращением
вокруг оси
фигуры, расположенной в первом квадранте
и ограниченной параболой
![]() ,
прямой
,
прямой
![]() и осью
.
Сделать рисунок фигуры вращения.
и осью
.
Сделать рисунок фигуры вращения.
Решение.
Построив линии, получим фигуру вращения (рис. 14).
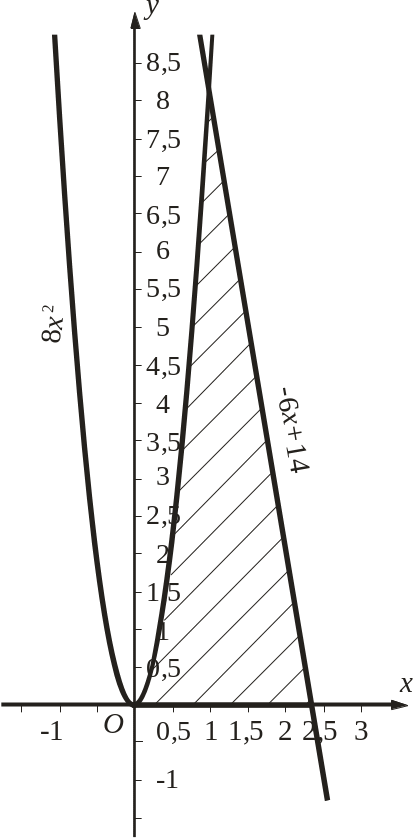
Рис. 14. Фигура вращения
Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого приравняем правые части их уравнений:
![]() .
.
Решим полученное квадратное уравнение.
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Первому
квадранту соответствует корень
![]() .
.
Найдем
абсциссу точки пересечения прямой
с осью
,
решив уравнение
![]() ,
откуда
,
откуда
![]() .
.
Таким
образом, тело ограничено при
![]() поверхностью, образованной вращением
параболы
вокруг оси
,
а при
поверхностью, образованной вращением
параболы
вокруг оси
,
а при
![]() –
вращением прямой
.
–
вращением прямой
.
Объем тела вращения вычисляется по формуле:
![]() ,
,
где
,
![]() ,
,
![]() ,
,
![]() –
уравнения линий, ограничивающих
криволинейную трапецию, которая вращается
вокруг оси
.
–
уравнения линий, ограничивающих
криволинейную трапецию, которая вращается
вокруг оси
.
Тогда искомый объем:
 .
.
Для вычисления второго интеграла применим метод подведения под знак дифференциала:

![]() (куб.
ед.).
(куб.
ед.).
Ответ:
![]() (куб. ед.).
(куб. ед.).
Задание № 5.
Вычислить
длину дуги кривой
 где
где
![]() .
.
Решение.
Если уравнение кривой задано в параметрической форме:
![]()
где
![]() ,
то длина дуги кривой вычисляется по
формуле:
,
то длина дуги кривой вычисляется по
формуле:
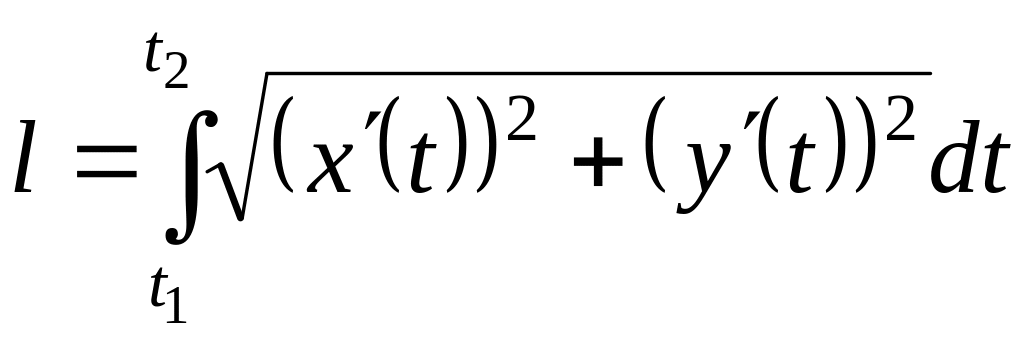 .
.
Найдем
![]() и
и
![]() :
:
![]()
![]() ,
,
![]()
![]() .
.
Тогда
![]()
![]() (ед.).
(ед.).
Ответ:
![]() (ед.).
(ед.).
Задание № 6.
Вычислить несобственные интегралы или установить их расходимость.
1)
![]() ;
;
2)
![]() .
.
Решение.
1) Несобственный интеграл с бесконечным верхним пределом интегрирования вычислим с помощью предельного перехода:
![]()
![]() .
.
2)
Так как
![]() является точкой разрыва подынтегральной
функции
является точкой разрыва подынтегральной
функции
![]() ,
то интеграл
является несобственным.
,
то интеграл
является несобственным.
Вычислим его с помощью предельного перехода:

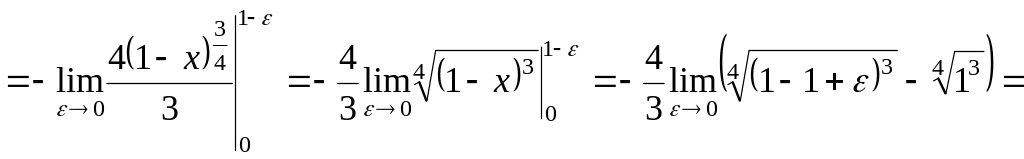
![]() .
.
Защита РГР № 4 «Определенный интеграл и его применение»
Теоретические вопросы:
Определение определенного интеграла;
Свойства определенного интеграла;
Вывод формулы Ньютона-Лейбница;
Геометрический смысл определенного интеграла;
Формула интегрирования по частям в определенном интеграле;
Вычисление площади плоской фигуры с помощью определенного интеграла;
Вычисление длины дуги кривой с помощью определенного интеграла;
Вычисление объема тела вращения с помощью определенного интеграла;
Несобственные интегралы.
Задачи для подготовки к защите РГР:
№ 1. Вычислить определенные интегралы:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
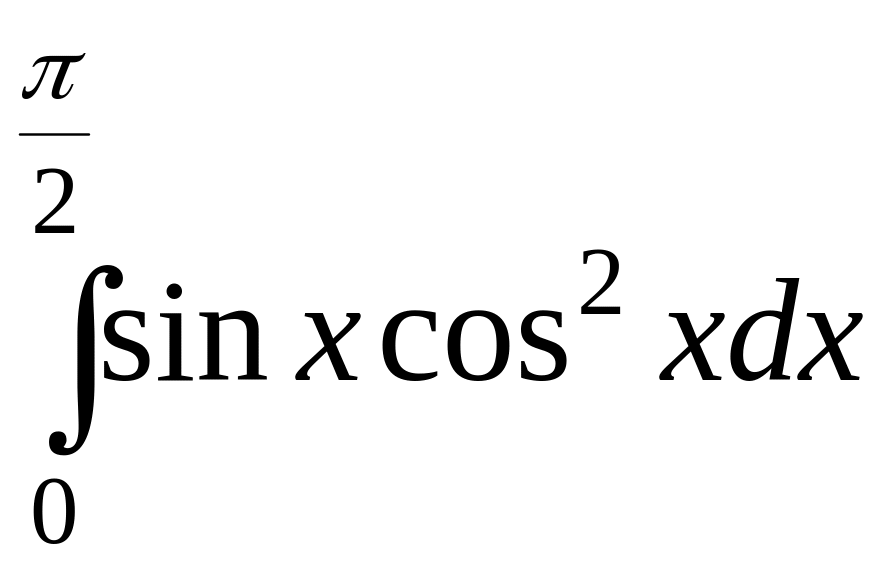 ;
;
9)
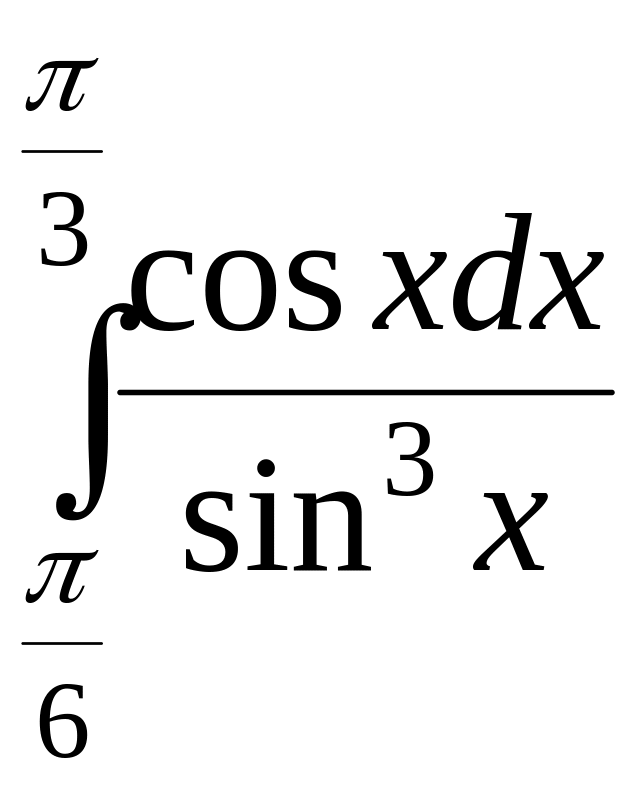 ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
 ;
;
13)
; 14).![]() .
.
№ 2. Вычислить площадь фигуры, ограниченной линиями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() и
и
![]() ;
;
8)
![]() и
и
![]() .
.
Изобразить фигуру.
№ 3. Вычислить площадь фигуры, ограниченной линией, заданной в полярной системе координат:
1)
![]() ;
;
2)
![]() ,
,
![]() .
.
Изобразить фигуру.
№ 4. Вычислить длину дуги кривой:
1)
![]() ;
от
;
от
![]() до
до
![]() ;
;
2)
![]() от
от
![]() до
до
![]() .
.
№ 5. Вычислить длину дуги кривой, заданной параметрически:
1)
![]() где
где
![]() ;
;
2)
![]() где
где
![]() .
.
№ 6. Вычислить длину дуги кривой, заданной в полярной системе координат:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() .
.
№ 7. Вычислить
объем тела, полученного вращением вокруг
оси
![]() фигуры,
расположенной в I четверти и ограниченной
параболой
фигуры,
расположенной в I четверти и ограниченной
параболой
![]() ,
прямой
,
прямой
![]() и осью
.
Сделать рисунок.
и осью
.
Сделать рисунок.
№ 8. Вычислить
объем тела, полученного вращением вокруг
оси
![]() фигуры, ограниченной гиперболой
фигуры, ограниченной гиперболой
![]() ,
прямыми
,
прямыми
![]() ,
,
![]() и осью
.
Сделать рисунок.
и осью
.
Сделать рисунок.
№ 9. Вычислить
объем тела, полученного вращением вокруг
оси
фигуры, ограниченной линиями
![]() .
Сделать рисунок.
.
Сделать рисунок.
№ 10. Вычислить объем тела, полученного вращением вокруг оси фигуры, ограниченной линиями .
№ 11. Вычислить несобственные интегралы или установить их расходимость:
1)
![]() ; 2)
; 2)
![]()