7.2. Несобственные интегралы с параметром

Перейдём к изучению несобственных интегралов, зависящих от параметра. Наиболее простая запись такого интеграла – это по-прежнему

но здесь либо b = ∞, либо функция f(x,y) не ограничена в окрестности точки x = b. Для краткости будем говорить, что интеграл имеет особенность в точке x = b. Переменная y принимает значения на отрезке [c, d] (или на неограниченном промежутке, например [c, ∞)).

При изучении несобственных интегралов вида мы

обращали внимание на их аналогию с числовыми рядами. Аналогичны не только термины («сходится», «расходится»), но и существо дела. Например, признаки сравнения для несобственных интегралов и числовых рядов формулируются и доказываются одинаково. В интегральном признаке сходимости числовых рядов прямо сопоставляются несобственный интеграл и числовой ряд:

Похожая ситуация имеет место и для несобственных интегралов, зависящих от параметра. Но здесь аналогия устанавливается не с числовыми, а с функциональными рядами:

Важным в теории было понятие равномерной сходимости. Оказывается, и здесь оно играет ключевую роль.

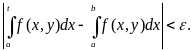
П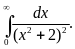 ример 1. Вычислить

Решение. Рассмотрим интеграл, зависящий от параметра:

Он легко вычисляется:

Применим к нему теорему о дифференцировании по параметру:

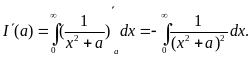
С другой стороны,

Значит,

Дифференцирование по параметру законно, так как при a > 0

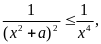
и сходящийся интеграл является мажорирующим для

Поэтому

П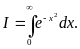 ример 2. Вычислить интеграл Эйлера-Пуассона

Решение. Сделаем замену переменной: x = ut, где u > 0 – параметр.

Тогда
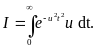