2.3. Метод потенціалів
Припустимо,
що оплату перевезень здійснюють спільно
виробник і споживач. Вони вносять так
звані платежі:
виробник платежі
,
споживач платежі
.
Суму цих платежів назвемо псевдовартістю:
|
(2.3) |
.При цьому виконуються умови: у всіх базисних клітинах псевдовартість повинна дорівнювати вартості перевезень:
|
(2.4) |
,де
– множина базисних клітин.
Технологія
призначення платежів проста завдяки
такому факту. Всього платежів
,
а рівнянь типу (2.4) – стільки, скільки
базисних клітин, тобто
,
значить, один платіж можна брати довільно,
наприклад,
.
Знайдемо платежі в таблиці 2.3 з лекції
1 і отримаємо табл. 2.4.
Таблиця 2.4
|
|
|
|
|
|
|
9 10 – |
2 10 |
6 15 + |
2 7 |
0 |
|
12 7 |
5 15 |
9 20 |
5 4 |
3 |
|
14 4
|
7 6
|
11 10 – |
7 30 |
5 |
|
9 |
2 |
6 |
2 |
|
Якщо
,
то
,
.
Але тоді
,
щоб
.
Далі:
,
щоб
,
;
.
Знайдемо псевдовартості для вільних
клітин і запишемо їх у верхніх лівих
кутах клітин.
Бачимо, що у клітині (3, 1) ціна циклу
.
Для
цієї клітини доцільно побудувати цикл
(позначений у табл. 2.4). Цей цикл має деяку
особливість: величина
одночасно наявна у двох від’ємних
клітинах. Згідно з приміткою до теореми
2 лише одну клітину робимо вільною.
Здійснимо перенесення по циклу і знайдемо
нове значення цільової функції:
|
|
|
|
|
|
|
9 0 - |
10
|
6 25 + |
7
|
0 |
|
7
|
5 15 |
9 20 - |
15 4 + |
3 |
|
4 10 + |
6 |
11
|
7 30 - |
-5 |
|
9 |
2 |
6 |
12 |
|
.
Отримаємо табл. 2.5 і знову призначимо платежі.
Таблиця 2.5
Як
видно з табл. 2.5, платежі можуть бути і
від’ємними (
).
Розглянемо цикл для клітини (2; 4). Ціна
циклу
,
але
.
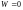Отже, цикл доцільний, хоча величина
не зміниться. Його сенс у тому, що
структура базису буде іншою, і це приведе
до поліпшення плану у майбутньому. У
таблиці 2.6 клітина (1; 1) стала вільною, а
в нову базисну клітину (2; 4) записуємо
0.
Таблиця 2.6
|
|
|
|
|
|
|
9
|
10
|
6 25 |
7
|
0 |
|
7
|
5 15 - |
9 20 |
4 0 + |
3 |
|
4 10 |
8 6+ |
11
|
7 30 - |
6 |
|
-2 |
2 |
6 |
1 |
|
Наведемо табл. 2.7
Таблиця 2.7
|
|
|
|
|
|
|
9
|
10
|
6 25 |
7
|
0 |
|
7
|
5
|
9 20 - |
4 15 + |
3 |
|
4 10 |
6 15 |
12 11 + |
7 15 - |
6 |
|
-2 |
0 |
6 |
1 |
|
Тепер залишається лише одна клітина (3;3) з від’ємною ціною:
.
Маємо:
,
і таблицю 2.8
Таблиця 2.8
|
|
|
|
|
|
|
–11 9
|
1 10
|
6 25 |
1 7
|
0 |
|
2 7
|
4 5
|
9 5 |
4 30 |
3 |
|
4 10 |
6 15 |
11 15 |
6 7 |
5 |
|
–1 |
1 |
6 |
1 |
|
У табл. 2.8 всі псевдовартості менші за вартості, тому план оптимальний:
всі
інші
;
.
Спостерігаємо
той неочевидний факт, що перевезення
з
виявиться доцільним, в той час як багато
клітин з меншою вартістю залишилися
пустими.