Модуль № 2 "Спеціальні задачі математичного програмування та їх застосування в економічному аналізі” Лекція №1. Постановка транспортної задачі. Знаходження допустимого базисного плану.

1.1. Постановка задачі

Так звана транспортна задача (ТЗ) є частинним випадком загальної задачі лінійного програмування. Її прості в математичному аспекті умови дозволяють застосувати значно більш ефективні методи розв’язування, ніж для загальної задачі.

Один із варіантів постановки ТЗ полягає у знаходженні оптимального плану перевезень деякого однорідного вантажу з пунктів виробництва або складів в пунктів призначення (споживання) .

Оптимізація плану перевезень полягає у мінімізації загальної вартості перевезень або мінімального часу їх доставки.

Сформулюємо математичну постановку цього варіанту задачі (з мінімізацією загальної вартості).

Задано:

• обсяги виробництва (запаси), що дорівнюють , у пунктах , ;

• обсяги споживання (заявки), що дорівнюють , у пунктах , ;

• матриця 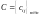, де – затрати на перевезення одиниці вантажу з пункту до пункту .

Треба знайти множину , що містить значень , де - обсяг перевезень з пункту в пункт , таку, що мінімізує функцію

(1.1)

за умов:

(1.2)

(задоволення всіх заявок);

(1.3)

(реалізація всіх запасів)

(1.4)

(зворотні перевезення від до усуваються).

У найпростішому варіанті повинна виконуватися ще умова рівності суми заявок і запасів:

. (1.5)

Цю умову можна записати ще й так:

, (1.6)

звідки видно, що одне з рівнянь систем (1.2) і (1.3) не є незалежним, оскільки є наслідком решти.

У цьому варіанті задача називається закритою. Якщо умова (1.5) не виконується, задача називається відкритою. Вона легко зводиться до закритої.

Означення. Множина , що задовольняє умови (1.2), (1.3), (1.4), називається допустимим планом. Легко бачити, що ранг матриці системи рівнянь (1.2) і (1.3) у невиродженому випадку дорівнює , але умова (1.5) або (1.6) зменшує ранг на одиницю, і таким чином ранг системи (1.2), (1.3), (1.6) дорівнює . Звідси в системі може бути базисних змінних. Кількість вільних змінних дорівнює . Розглядаючи загальну ЗЛП (п. 2.5), видно, що в оптимальному плані вільні змінні повинні дорівнювати нулю.

Означення. Допустимий план, у якому не більше, як ненульових величин , називається базисним або опорним.

Означення. Базисний план, що мінімізує функцію (1.1), називається оптимальним.

Твердження. На відміну від загальної задачі ЛП, ТЗ завжди має допустимий і оптимальний плани.

1.2. Розв’язування транспортної задачі

Розв’язування транспортної задачі відбувається за допомогою так званої транспортної таблиці, загальний вигляд якої подано у табл. 8.1. У клітинках з індексами i, j таблиці записано величини (у верхньому правому куті); у процесі розв’язування в деяких клітинах з’являться ненульові , а також додаткова інформація.

Таблиця 1.1

Пункти відправлень	Пункти призначення							Запаси
			...		…
			...		…
			…		…
…	…	…	…	...	…	...	...
			…	,	…
…	...	…	…	…	…	...	…
			…		…
Заявки			…		…

Рядки таблиці відповідають умовам (1.3), стовпчики – умовам (8.2).

Розв’язування ТЗ пояснимо на прикладі конкретної задачі, наведеної в табл. 1.2. Тут , .

Приклад 1.1. Розв’язати ТЗ, умова якої задана в таблиці 1.2.

Таблиця 1.2

Пункти відправлень	Пункти призначення				Запаси
	9	10	6	7		25
	7	5	9	4		35
	4	6	11	7		40
Заявки	10	15	45	30

Розв’язування ТЗ містить два етапи:

• побудова опорного плану;

• побудова оптимального плану.
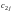