5. Практическая часть

Рассмотрим теперь на практике, какие бывают задачи и как можно исследовать функцию на наибольшее и наименьшее значение.

Задача №1

Укажите наибольшее число, принадлежащее промежутку

а) [-15; -11];

б) [5; 7);

в) [5; 7].

Так же в 7 классе а теме «Линейная функция» Мордкович А.Г. вводит само понятие наибольшего и наименьшего значения функции на отрезке. Он рассматривает линейную функцию y на отрезке [0;6].

Рис. 1

Соответствующий отрезок графика выделяется на чертеже. Замечается, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 - это и есть наибольшее значение заданной линейной функции на отрезке. Записывается это следующим образом . Далее отмечается, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке части прямой, равна 4 - это и есть наименьшее значение линейной функции на отрезке [0; 6]. Записывают так .

Задача №2

Постройте график функции . С помощью графика найдите:

а) значения у при х = 4; 7; 16;

б) значения х, если у = 0; 1; 3;

в) наименьшее и наибольшее значения функции на отрезке [0; 4];

г) при каких значениях х график функции расположен выше прямой

у = 1; ниже прямой у = 1.

Найдите наименьшее и наибольшее значения функции :

а) на отрезке [0; 4];

б) на луче

в) на отрезке [1; 9];

г) на полуинтервале (2; 9].

Постройте график функции . С помощью графика найдите:

а) значения у при х = -3; 1; 6;

б) значения х если у = 3; -1; -6;

в) наименьшее и наибольшее значения функции на отрезке [-3; -1];

Решите двойное неравенство и укажите наименьшее и наибольшее целые числа, которые являются его решениями.

Найдите наименьшее целое число, удовлетворяющее системе неравенств

Задача №3

Определить наибольшее и наименьшее значение функции на промежутке.

1.  T

Функция определена на всем множестве действительных чисел

T

Найдем производную функции

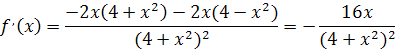
T

Приравняем ее к нулю и определим критические точки

T.

Проверим знак производной слева и справа от найденной точки

T

T

Производная при переходе через точку  T меняет знак с положительного «+» T на отрицательный «-« T, следовательно она является точкой локального максимума.

Найдем значение функции в точке  

T

и на краях отрезка

;

T .

T

Таким образом, функция достигает максимума в точке локального экстремума  T и минимума на одном из краев отрезка  T.

Задача №4

.

На заданном промежутке функция определена; вычислим ее производную

.

Приравнивая нуля найдем критическую точку

.

Заданная точка принадлежит отрезку. Найдем значения функции во всех точках

.

T .

T .

Функция приобретает максимум и минимум в точках

; .

Задача №5

.

T

Функция определена везде, потому приступим сразу к вычислению производной

.

T

Приравняем ее к нулю и находим критические точки

;

T .

Найдем значения функции во всех подозрительных на экстремум точках

;

;

T

T ;T

T .T

Из полученного набора значений следует, что функция принимает максимум и минимум на краях отрезка

; .

T T

Задача №6

Найти наибольшее и наименьшее значение функции T на отрезке [0;5]. T

Решение. 

Находим производную функции:

Находим точки, в которых производная равна нулю:

Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку [0;5]. Оба значения лежат в этом промежутке.

Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:

y(0)=4; y( )= 3,92; y(5)=454

Таким образом,

; .

T

Ответ: ;

Задача №7

Найти наибольшее и наименьшее значения функции на заданном отрезке T.

Решение:

В этой задаче используется теорема о том, что непрерывная функция достигает своего наибольшего и наименьшего значений на отрезке: либо в критических точках, где производная обращается в нуль или не существует; либо на концах отрезка. Таким образом, для того, чтобы найти наибольшее и наименьшее значения функции на данном отрезке, необходимо найти её значения в критических точках и на концах отрезка, а затем сравнить эти значения. 

Перепишем выражение функции в виде:

Найдем производную функции в виде: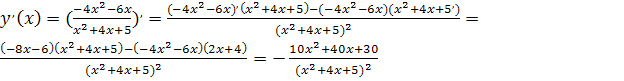

Найдем критические точки:

. Отсюда 10 или .

T         Вычислим значения функции в найденной точке и на концах отрезка:

T   TСравнивая полученные значения, можем заключить, что наибольшее значение равно , Tа наименьшее значение равно .  T

Ответ: Наибольшее значение функции на отрезке равно .

Наименьшее значение функции на отрезке равно .

Задача №9

С помощью производных высших порядков найти экстремум функции .

Решение: 

Находим производную функции: . Найдем критические точки: ,

;

;

T

Находим , вычисляем ,

Значит T– точки минимума функции;  ,

T Значит T– точки максимума функции.

Задача №9

Найдите наименьшее значение функции   на интервале

(0; 2)

Решение:

1. ;

2. ;

3. 

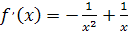На интервале (0; 2) данная функция непрерывна, имеет единственный экстремум в точке  x=1 и этот экстремум - минимум. Следовательно,  T - наименьшее значение данной функции на интервале (0; 2)

Ответ: 1

Задача №10

Основание пирамиды - равнобедренный прямоугольный треугольник. Все боковые рёбра пирамиды равны  T. Найдите наибольший возможный объём такой пирамиды.

Решение:

Примем высоту DO данной пирамиды за x, где T. Из прямоугольного треугольника ADO находим AO2=3-x2 T, а из равнобедренного треугольника  ACO находим AC2=2AO2 =2(3-x2) T. Таким образом, требуется найти наибольшее значение функции V(x)= TTTна интервале (0; ) T.

; T; T

На интервале T(0; ) функция  V(x) непрерывна, имеет единственный экстремум в точке x = 1 и этот экстремум - максимум.

T

Следовательно, V(1)= TT - наибольшее значение данной функции на интервале T(0; ).

Ответ: 

Замечание:  Рассмотренный выше алгоритм нахождения наибольшего (наименьшего) значения функции на интервале применим и для нахождения наибольшего (наименьшего) значения функции на отрезке, если функция непрерывна на этом отрезке и имеет на нём единственный экстремум.

Задача №12

Найдите наименьшее значение функции 

T 

Решение:

Найдём область определения данной функции: На множестве  (-3; 2] имеем: ;   T Следовательно, T T T Таким образом, требуется найти наименьшее значение функции T  на множестве (-3; 2]. Найдём производную функции  f(x): T . Решим уравнение T  на множестве  (-3; 2]: T            T Функция  T, заданная на множестве R, возрастает на отрезке [-3; -2], следовательно, для любого  T выполняется условие . Значения функций g(x) и  f(x) совпадают на множестве (-3; 2], значит, для любого  T выполняется условие . T На отрезке [-2;2] функция  f(x) непрерывна, имеет единственный экстремум и этот экстремум - минимум. Следовательно, T - наименьшее значение функции  f(x) на отрезке [-2; 2]. Таким образом, число 48 - наименьшее значение функции  f(x).

Ответ: 48

Задача №12

Найдите наименьшее значение функции  на отрезке .

Решение:

Напомним, что любая функция принимает наименьшее или наибольшее значение тогда, когда ее производная равна нулю или не существует. 

Найдем производную и приравняем ее к нулю. 

Видим, что производная равна нулю при x₁=0 и x₂=5

Заметим, что при х ∈ [4; 5) производная y´(x)<0 и значит функция убывает при х ∈ (5; 6] производная y´(x)>0 и значит функция возрастает

То есть при х = 5 y´(x) меняет знак с - на +, значит при х = 5 наименьшее значение: у(5) = (5² - 7*5 + 7) * е^5-5 = (25 - 35 + 7) * е⁰ = -3*1 = -3.

Ответ: -3.

Задача №14

Найти наибольшее и наименьшее значение функции на отрезке .

Решение:

Поскольку , критические точки f(x) совпадают с теми, для которых производная равна нулю. Легко найти, что это точки . Из того, что , следует, что знак совпадает со знаком выражения , и можно нарисовать картинку поведения f(x) на отрезке

+ - ₊

-2 -1 1 2

Отсюда видно, что наименьшее значение принимает либо в точке -2, либо в точке 1.

Поскольку , наименьшее значение функции на отрезке равно -16. Наибольшее значение функции есть одно из двух чисел и . Поскольку , наибольшее значение на равно 24.

Ответ: ; .

Задача №15

Найдите наибольшее значение функции на отрезке .

Решение:

Напомним, что любая функция принимает наименьшее или наибольшее значение тогда, когда ее производная равна нулю или не существует.

Найдем производную .

.

Заметим, что при любых , так как , как мы знаем, это выполнимо всегда, так как .

Делаем такой вывод: так как производная при , то функция возрастает на этом отрезке и наибольшее значение будет при наибольшем x их этого отрезка - это .

Подставим в и получим , так как .

Ответ: 7.

Задача № 16

Найдите наибольшее значение площади прямоугольника со сторонами параллельными осям координат, и с диагональю OP, где О – начало координат, а Р – точка на графике функции .

Решение:

Длины сторон прямоугольника равны положительным координатам точки Р. Поэтому его площадь равна их произведению: . Исследуем функцию ,   с помощью производной.

.

Так как , а по условию , то – единственная критическая точка. Найдем значения функции S в концах отрезка [0,2; 1] и сравним их с .

Так как , то . Так как , то , , и .

Ответ: 13.

Заключение

Над изучением этой темы работали многие ученые и философы. Много лет назад появились такие термины как функция, график, исследование функции и до сих пор они сохранились, приобретая новые черты и признаки.

Я выбрала эту тему, потому что мне было очень интересно узнать историю возникновения исследования функции. Мне кажется, что многим было бы интересно побольше узнать о функции, о ее свойствах и преобразованиях. Сделав эту курсовую работу, я систематизировала свои навыки пополнила свой запас знаний об этой теме.

Список используемой литературы

1. Мордкович А.Г. Алгебра и начала математического анализа 10-11кл. – Москва, 2009.

2. Мордкович А.Г. и др. Задачник по алгебре и началам математического анализа 10-11кл. – Москва,2009.

3. Колмогоров А.Н., Абрамов А.М. и др. Алгебра и начала математического анализа 10-11кл. – Просвещение, 2008.

4. Башмаков М.И. Алгебра и начала анализа 10-11 кл. – Москва, 1992.

5. Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа 10-11кл. – Москва, 2010.

6. Виленкин Н.Я. Производная и задачи на экстремум // Квант,1978 №6 с. 60-64.

7. Гусак А. А.. Высшая математика. Учебное пособие для студентов вузов в 2-х томах. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).

8. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.

9. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000 г.

10. Ткачук В.В. Математика абитуриенту М: МЦНМО, 2008.

28