Эл.техн ЛР2

Лабораторная работа № 2

Исследование электрических цепей синусоидального тока.

Резонанс напряжений

1. Цель работы

Исследование явления резонанса напряжений при последовательном соединении катушки индуктивности и конденсатора. Исследование соотношения между током и напряжением в электрической цепи синусоидального тока с катушкой индуктивности.

2. Пояснение к лабораторному стенду

Работа выполняется на универсальном лабораторном стенде. С помощью перемычек собирается электрическая цепь (рис. 1). Резонанс напряжений достигается за счет введения в катушку ферромагнитного сердечника и плавного изменения его положения.

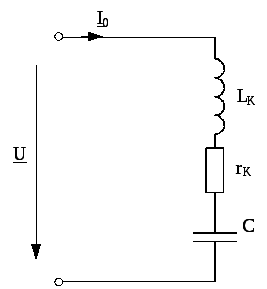
Рис.1

Измерение сдвига фаз φ между U и I осуществляется фазометром.

Резонансом в электрических цепях называется явление, при котором входное реактивное сопротивление всей цепи равно нулю. При этом ток и напряжение на входе цепи совпадают по фазе, а эквивалентное сопротивление всей цепи будет чисто активным.

Для режима резонанса в цепи, представленной на рис. 1, характерна возможность возникновения, равных по модулю напряжений на катушке индуктивности и конденсаторе, существенно превышающих напряжение питания цепи U (отсюда название – резонансное напряжение).

Условие возникновения резонанса напряжений в последовательном контуре

x_L = x_C, при этом .

Из этого соотношения видно, что резонанса в цепи можно достичь, варьируя либо частотой приложенного напряжения, либо параметрами цепи «L» и «C», либо тем и другим одновременно.

Если в цепи возник резонанс напряжений, то резонансная частота равна

.

Резонансный контур характеризуется следующими параметрами:

• волновое сопротивление ;

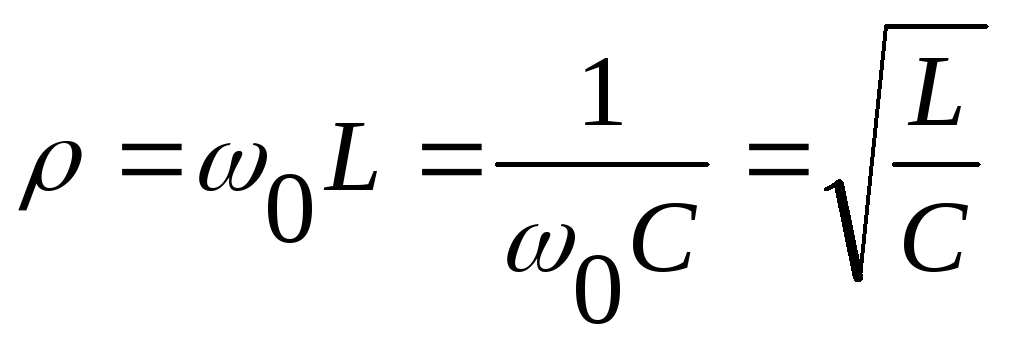• добротность контура , где .

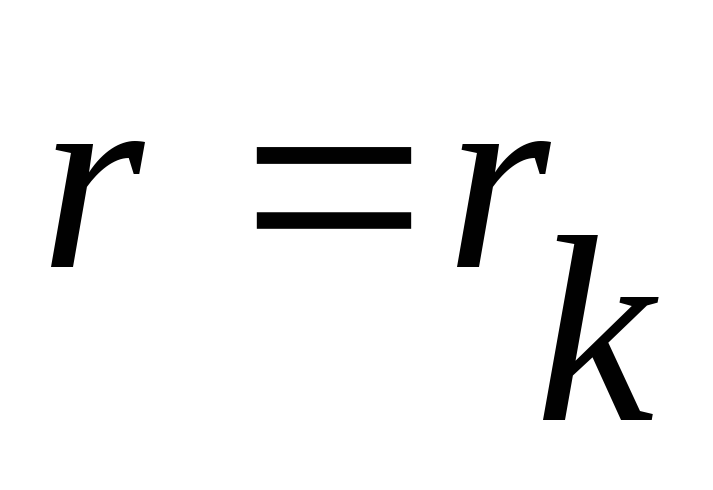Исследование явления резонанса в данной работе осуществляется изменением положения ферромагнитного сердечника внутри катушки индуктивности.

Так как при резонансе полное сопротивление цепи минимальное (Z_Э = r_k), то при постоянстве действующего значения напряжения момент наступления резонанса можно определить по максимальному току в исследуемой цепи:

.

Падения напряжения на катушке индуктивности и на конденсаторе рассчитываются следующим образом:

После определения электрических параметров элементов цепи при резонансе производятся измерения в схеме с одной катушкой индуктивности без конденсатора (рис. 2).

Реальная катушка индуктивности обладает электрическим сопротивлением r_K и может быть представлена эквивалентной схемой, состоящей из последовательно включенных катушки индуктивности L_K и активного сопротивления r_K (рис. 2). Векторная диаграмма для такой схемы приведена на рис 3.

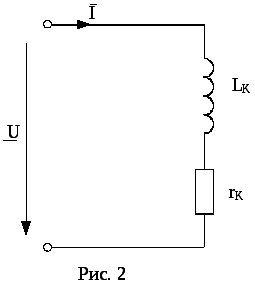
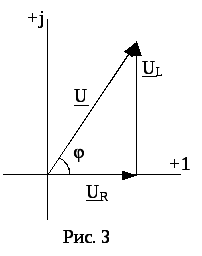
Ток в одноконтурной цепи, состоящей из последовательно соединенных элементов (рис. 2), находится по закону Ома.

,

где Z – входное комплексное сопротивление цепи, равно сумме сопротивлений отдельных ее элементов:

.

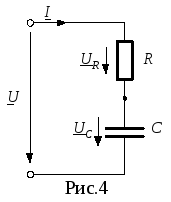
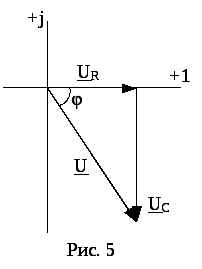
На рис. 4 показана цепь, состоящая из последовательно включенных конденсатора С и активного сопротивления R= r_K, а на рис. 5 ее векторная диаграмма. Расчет такой цепи аналогичен предыдущему, а эквивалентное сопротивление цепи равно

.

3. Расчетные соотношения для исследуемой электрической цепи

В однофазных электрических цепях в большинстве случаев действуют ЭДС, изменяющиеся по синусоидальному закону

,

где e – мгновенное значение ЭДС;

E_m – амплитудное значение;

– угловая частота;

f – частота;

_e – начальная фаза.

Токи и напряжения в таких цепях синусоидальны:

;

.

Фазовый сдвиг между напряжением и током .

Наряду с мгновенным и амплитудным в электротехнике используется понятие о среднеквадратичном (действующем) значении переменного тока, напряжения, ЭДС.

.

Действующее значение синусоидального тока

.

В большинстве случаев расчет цепей синусоидального тока производят комплексным методом, который позволяет осуществить переход от тригонометрических уравнений к алгебраическим, составленным относительно комплексов тока и напряжения.

Известно, что синусоидально изменяющаяся величина может быть условно (символически) представлена в виде комплексного числа A. Это лежит в основе замены синусоидальных функций вращающимися векторами.

Совокупность векторов, изображающих синусоидально изменяющиеся токи, напряжения, ЭДС некоторой электрической цепи, называется векторной диаграммой. Векторные диаграммы строятся для момента времени t = 0. Комплексные сопротивления индуктивности и емкости соответственно можно найти как

; .

Зная комплексные сопротивления можно определить величины индуктивности и емкости элементов

.

Величины действующих значений входных напряжения U и тока I при частоте f = 50 Гц определяются во время измерений. Их следует рассматривать в качестве исходных значений, поэтому все расчеты проводятся по окончанию измерений.

4. Экспериментальная часть работы

1. Собрать схему (рис. 1).

2. При заданном преподавателем напряжении источника U изменением положения сердечника катушки индуктивности по максимуму тока в цепи добиться резонанса напряжений и провести измерения действующих значений тока, падения напряжения на конденсаторе, а также угла сдвига фаз. Результаты измерений занести в таблицу 1.

3. Собрать схему (рис. 2).

4. При заданном преподавателем напряжении источника U провести измерения действующего значения тока и угла сдвига фаз. Результаты измерений занести в таблицу 2.

5. Собрать схему (рис. 4). Установить сопротивление R равным по величине активному сопротивлению катушки индуктивности r_K.

6. При заданном преподавателем напряжении источника U провести измерения действующих значений тока и падений напряжений на элементах цепи, а также угла сдвига фаз. Результаты измерений занести в таблицу 3.

Таблица 1

	U, В	I, мА	φ, град	UС, В	rK, Ом	L, Гн
Опыт
Расчет

Таблица 2

	U, В	I, мА	φ, град	L, Гн
Опыт
Расчет

Таблица 3

	U, В	I, мА	φ, град	UС, В	UR, В	C, мкФ
Опыт
Расчет

4. Расчетная часть работы

1. Используя результаты проведенных измерений, занесенных в табл.1, рассчитать величину активного сопротивления катушки индуктивности, а также падение напряжения на конденсаторе и индуктивность катушки при резонансе. Полученные данные занести в таблицу 1. Сравнить результаты, снятые экспериментально с расчетными, где в качестве исходных значений использовать измеренные значения U и I. Построить векторные диаграммы токов и напряжений для схемы рис. 1.

2. Используя результаты проведенных измерений, занесенных в табл.2, подсчитать индуктивность катушки без сердечника. Расчетные данные занести в таблицу 2. Сравнить результаты, снятые экспериментально с расчетными. Построить векторные диаграммы токов и напряжений для схемы рис. 2.

3. Используя результаты проведенных измерений, занесенных в табл.3, произвести расчет падений напряжений на конденсаторе и на сопротивлении. Полученные данные занести в таблицу 3. Сравнить результаты, снятые экспериментально с расчетными. Построить векторные диаграммы токов и напряжений для схемы рис. 3.

5. Содержание отчета

1. Цель работы.

2. Схемы исследуемых цепей (рис. 1, 2, 4).

3. Расчетная часть.

4. Таблицы 1, 2,3 с расчетными и опытными данными.

5. Векторные диаграммы исследуемых электрических цепей.

Контрольные вопросы

1. В каких цепях возможен резонанс напряжений и условия его возникновения?

2. Основные параметры резонансного контура.

3. Каким образом можно повысить добротность резонансного контура?

4. Какие существуют способы достижения резонанса напряжений?

5. Определить характер цепи в диапазоне изменения частот генератора источника от 0 до резонансной?

6