
ПОРЯДОК планирования 3
.docxПОРЯДОК ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ
|
(Целевая функция, функцию отклика, зависимая переменная, реакция системы на воздействие факторов, содержание целевой функции) Yi - ________________________ |
Проходка за рейс |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(Независимые переменные, от которых зависит целевая функция) Содержание факторов X1 - ______________________________________ X2 - ______________________________________ |
Скорость вращения долота, Плотность раствора Осевое усилие |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Минимальное значение фактора Хi min = ____________ Максимальное значение фактора Xi max = ____________ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Среднее значение фактора определяется по формуле
X1 0= __________ X2 0 = __________ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Интервал варьирования определяется по формуле: dxi = Xi 0 – Xi min = Xi max - Xi 0. = ___________ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Для этого необходимо составить таблицу натуральных значений факторов
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Нормированные значения определяются формулой
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рекомендуется проводить по каждому опыту равномерное количество дублирующих опытов. В общем случае их должно быть не менее 3…5. Провести по 5 параллельных опытов на каждую комбинацию факторов |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Определить численные значения функции отклика в зависимости от комбинации значений факторов и составить матрицу с результатами экспериментов
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
при m - число повторных опытов
|
Среднее значение выходной величины Yi в каждой точке определим по формуле (1) при (m = 3) Y1 = (43+35+48)/3 = 42 Y2 = (90+86+94)/3 = 90, Y3 = (10+16+16)/3 = 14, Y4 = (56+54+58)/3 = 56 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
m – количество параллельных опытов в строке матриц |
Определим по формуле (2) построчную дисперсию S2{y1}= [(43–42)2 +(35–42)2 + (48–42)2]/2 = 43, S2{y2}= [(90–90)2 +(86–90)2 + (94–90)2]/2 = 16, S2{y3}= [(10–14)2 +(16–14)2 + (16–14)2]/2 = 12, S2{y4}= [(56–56)2 +(54–56)2 + (58–56)2]/2 = 4. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Проверить однородность дисперсии с помощью критерия Кохрена |
Критерий (коэффициент) Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них. Определить критерий Кохрена по формуле
где smax – наибольшая величина дисперсии; si – дисперсия i-го опыта N – общее число опытов в матрице. В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выбрать среди всей совокупности рассчитанных построчных дисперсий число с максимальной дисперсией |
S2{yi}мах |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вычислить сумму всех построчных дисперсий |
ΣS2{yi} |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вычислить отношение максимальной дисперсии к сумме всех построчных дисперсий: |
|
По данным из нашего примера определим расчетное значение коэффициента Gp = 43/(43+16+12+4) = 0,57. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задать уровень значимости |
Для инженерных задач достаточен уровень значимости = 0,05 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить степени свободы |
степени свободы числителя (f1) f1= m –1 m – количество параллельных опытов в строке матриц степень свободы знаменателя (f2) f2 = N. N – общее число опытов в матрице |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cравнить расчетное значение коэффициента Кохрена с табличным значением Найти значение f1 в горизонтальном заголовке таблицы (выбирается столбец), Найти значение f2 выбирается слева в вертикальном заголовке таблицы (выбирается строка) Установить табличное величину критерия Gт на пересечении выбранных столбца и строки |
|
В соответствии с таблицей коэффициентов для = 0,05; f1 = 3 – 1 = 2; f2 = 4, Gт = 0,77 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Если выполняется условие: Gp < Gт, то с достоверностью 1 – все построчные дисперсии признаются однородными. В противном случае гипотезу отвергают. |
Gт = 0,77; Gт > Gp , т.е. условие выполняется |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рекомендуется линейная модель Y = b0 X0 + b1 X1 + b2 X2; Y = b0 X0 + b1 X1 + b2 X2 +b12 X12; (Х0 =1). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Оценка производится по t-критерию Стьюдента. Т.е. проверяется отклонение от нуля найденной оценки. Для каждого коэффициента bk вычисляется коэффициент Стьюдента:
где bk – коэффициент уравнения регрессии S{bk} – оценка среднего квадратичного отклонения погрешности определения коэффициента. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить оценку генеральную дисперсию воспроизводимости |
Оценкой дисперсии воспроизводимости S2в, характеризующая точность одного измерения, является средняя из всех построчных дисперсий
|
S2в = (43 + 16 + 12 + 4)/4 = 18,75 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить дисперсию коэффициентов, найденных по экспериментальным данным |
|
S2{bk} = 18,75/(4*3)= 1,56 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выполнить оценку дисперсию коэффициентов, найденных по экспериментальным данным |
Оценка
|
Для рассматриваемого примера S{bk} = 1,25. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вычислить критерий Стьюдента |
|
Определим расчетные значения коэффициента Стьюдента t0 = 50,5/1,25 = 40,4; t1 = 22,5/1,25 = 18; t2 = 15,5/1,25 = 12,4; t12 = 1,5/1,25 = 1,2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выбрать уровень статистической значимости |
= 0,05 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить число степеней свободы |
f = N (m – 1) |
f = 4 (3 – 1) = 8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти табличное значение коэффициента Стьюдента |
При выбранном уровне статистической значимости по таблицам распределения Стьюдента при числе степеней свободы f = N (m – 1) находят табличное значение коэффициента tтабл.
|
Из таблиц при уровне статистической значимости = 0,05 и числе степеней свободы f = 4 (3 – 1) = 8 , табличное значение коэффициента равно tт = 2,3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сравнить табличное значение с расчетным |
Если выполняется неравенство tтабл > tk, то принимается нуль- гипотеза, т.е. считается, что найденный коэффициент ak является статистически незначительным и его следует исключить из уравнения регрессии. |
Сопоставление расчетных значений tk с табличным tт. Неравенство выполняется для t12. Следовательно, можно предположить, что a12 статистически незначим и его можно исключить из уравнения регрессии |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение регрессии с учетом статистической значимости коэффициентов |
Y = b0 X0н + b1 X1н + b2 X2н |
Уравнение регрессии, содержащее статистически значимые коэффициенты, будет (в кодированной системе) Y' = 50,5 + 22,5x1 – 15,5x2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Проверить адекватность модели (пригодность для практического применения) |
Полученное уравнение регрессии необходимо проверить на адекватность исследуемому объекту.
Проверка адекватности выполняется по критерию Фишера Для этой цели необходимо оценить, насколько отличаются средние значения yi выходной величины, полученной в точках факторного пространства, и значения yi, полученного из уравнения регрессии в тех же точках факторного пространства. Адекватность модели проверяют по критерию Фишера F- критерию Fp= S2ад/S2в |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить значения функции отклика по уравнению регрессии |
|
Для рассматриваемого примера получаем: Y'1 =50,5 +22,5 (–1) – 15,5 (–1 ) = 43,5; Y'2 =50,5 +22,5 (+1) – 15,5 (–1 ) = 88,5; Y'3 =50,5 +22,5 (–1) – 15,5 (+1 ) = 12,5; Y'4 =50,5 +22,5 (+1) – 15,5 (+1 ) = 57,5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить оценку дисперсию адекватности |
где L – число значимых коэффициентов. |
Рассчитаем оценку дисперсии адекватности: S2ад = 3[(42 – 43,5)2 + (90 – 88,5)2 + (14 – 12,5)2 + (56 – 57,5)2]/(4 – 3) = 27 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить оценку генеральную дисперсию воспроизводимости |
Оценкой дисперсии воспроизводимости S2в, характеризующая точность одного измерения, является средняя из всех построчных дисперсий
|
S2в = (43 + 16 + 12 + 4)/4 = 18,75 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задать уровень значимости |
= 0,05 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вычислить критерий Фишера |
Fp= S2ад/S2в |
Fp = S2ад/S2в = 27/18,75 = 1,44. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить число степеней свободы |
fад = N – l fв = N(m - 1) |
fад = (4 – 3) = 1 и fв= 4 (3 – 1)=8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти табличные значения F- критерию |
Найденное расчетным путем Fp сравнивают с табличным значением Fт ,которое определяется при уровне значимости и числе степеней свободы fад = N – l - по горизонтали (f2) fв = N(m - 1) – по вертикали (f1)
|
Табличное значение коэффициента Фишера при уровне статистической значимости =0,05 и числе степеней свободы fад = (4 – 3) = 1 и fв= 4 (3 – 1)=8 будет Fт=5,32 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сравнить расчетное значение критерия с табличным и сделать вывод об адекватности модели |
Если Fp < Fт, то полученная математическая модель с принятым уровнем статистической значимости адекватна экспериментальным данным |
Следовательно, при выбранном уровне статистической значимости полученная в результате эксперимента регрессионная модель вида y' = 50,5 + 22,5x1 – 15,5x2 адекватна исследуемому объекту |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подставить в уравнение регрессии значения факторов в натуральных значениях по формуле
Y
= b0
+ b1
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 .
.
 .
.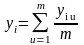 (1)
(1)



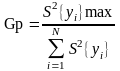




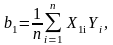









 ,
,
 + b2
+ b2
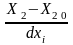 +b12
+b12