
2008
.doc|
1.Метод простой итерации. Решим
систему Ах=В (1), А= |
2.Метод Зейделя. Основная идея: при вычислении (К+1)-го приближения неизвестной Хi учитываются уже вычисленные ранее (К+1)-е приближение х1,х2,… Пусть дана приведенная лин. система Хi=βi+(∑ от j=1 до n)£ij*xiK Предпол. что К-е приближ. известны тогда (К+1) имеет вид Xn(K+1)=βn+(∑ отj=1 до n-1) £niXj(K+1) + £nnXn(K). Достаточное условие: 1) ∑(от i=1 до n)|Aij|<1 для любого y 2) ∑(от j=1 до n)|Aij|<1 для любого i Следствие: для сист. метод итер. сходит. если все модули диагонал. коэффициентов для каждого Ур-ия >, суммы модулей всех остал. коэффиц. |Aii| <(i≠j)|Aij|. |
||||||||||||||||||||||
|
3.Достаточные условия сходимости процесса итерации (доказать) Теорема: процесс итерации для системы Х=£x+β сх. к единств. решению если какая либо норма матр. £<1 или ||£||<1, xK=£x(K-1)+β, Док-во: постр. последов. приближен., таких, что XK=(£(K-1) +£(K-2)+…+ £+E)β+£KX0 Т.к. норма матр.<1, то норма £к→0, при к→∞ E+£+£2+…+£K-1=(∑от n=0 до K-1) £n| ||£||<1 |=(E-£)-1 X=lim(k→∞)Xк=lim[ (£(K-1) +£(K-2)+…+ £+E)β+£KX0 ]=(E-£ )-1β Сходимость доказана. |
4. Отделение корней уравнения. Отделение корней может происходить аналитически или графически. F(x)=0 X*- решение( F(X*) =0). Т. Если непрерывная ф-ция F(x) принимает значения различных знаков на [a,b], т.е F(a)*F(b)<0,то внутри этого отрезка содержится по крайней мере один корень уравнения F(x)=0 Метод половинного деления. Будем решать ур-ние f(x)=0 на [a,b], известно, что f(a)*f(b)<0. Найти X такое [x-x*] < ε. Метод состоит в последовательном построении интервалов [an, bn], вложенных друг в друга и содерж. реш. X*. Пусть a0=a, b0=b предпол. что [ai,bi]промежуток построения, причем f(ai)*f(bi)<0 т.е. X* Є[ai,bi] найдем (.)Ci=(ai+bi)/2. Если f(ci)=0 то (ci) точное решение, если f(ci) ≠ 0 то: либо 1) f(ai)*f(сi) < 0, тогда a(i+1)=ai*b(i+1)=ci, либо 2) f(ci)*f(bi)<0, тогда то a(i+1)=ci, b(i+1)=bi В любом случае получ. интервал вдвое меньше исходного, причем f(ai+1)*f(bi+1) < 0 Процесс заканчив. либо 1)|ai-bi|<E,тогда (F(ci)=0),ci- –выбир. любую (.) и приним. ее за решен. ОЦЕНКА точности. f(ai)*f(bi)<0; bn-an=1/2n X(с чертой)-an<=1/2n (b-a) k-кол-во шагов k=log2((b-a)/E)+1. Решение нелин. ур-ий . Решен. осущ. в 2 этапа 1) локализация корней , т.е. нахожд. промежутков [a,b] котор. принадл. корень ур-ия 2)уточнение корней ,т.е. решение с задан. точностью. |
||||||||||||||||||||||
|
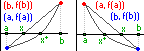
Метод хорд. Пусть
дана ф-ция F(x) = 0 на [a, b], причем F(a)*F(b) <
0. Для определенности предпол., что
F(a)<0 а F(b)>0, тогда поделим отрезок
[a,b] на F(a)/F(b). (x-a)/(b-a)=(y-f(a))/(f(b)-f(a));
Допустим X=X1,
y=0;
X1=a
– (f(a)
/ (f(b)-f(a)))*(b-a)
по этой ф-ле можно записать итерац.
процесс X1=a+h,
где
h1=-f(a)/(f(b)-f(a))
Докаж. сходим. итер. процесса будем
предполагать, что корень f(x)
определен и
1 2)
a<0
Т.е.1) неподвиж. тот конец , для кот. знак ф-ции совпад. со знаком втор. производ. 2)Послед. приближен. Xn лежат по ту сторон. X*, где f(x) имеет знак противоп знаку ее 2-ой произв. Критерий остановки |Xn+1 - Xn|< ε |
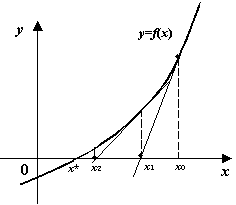
5. Метод касательных (Ньютона). y-y0=f ‘ (X)(X-X0) пусть f ‘ (X), f ‘ ‘ (X) –непрер. и сохр. опред. знаки на отрезке [a,b] пусть f ‘ ‘ (X)>0 и f(b)>0 (рис.) Ур-ие касат. y-f(Xn)= f ‘ (Xn)(X-Xn) y=0, X=Xn+1; X(n+1)=Xn-(f(Xn)/ f ‘ (Xn)) Исходя из геом. соображен. , вывед. тоже самое аналитич. X*=Xn+hn Прим. ф-лу Тэйлора 0=f(Xn+ hn)=f(Xn)+ hnf ‘ (Xn); hn =-f(Xn)/f ‘ (Xn) Выбор начал. точки f(X0)*f ‘ ‘ (X0)>0. Теорема: если f(a)*f(b)<0 причем втор. произв. сохр. знак на [a,b] , то исходя из любого начал. приближен. X0c[a,b] удовл. условию f(X0)* f ‘ ‘ (X0)>0 можно вычисл. корень ур-ия с любой степенью точности. Д-во: пусть f(a)<0 , f(b)>0 f ‘ (x)>0; f ‘ ‘ (x)>0(вогнута) т.е. f(b)* f ‘ ‘ (b)>0 ; X0=b-max точка.
X Геометрически прямая параллельная первой касательной . т.е. здесь касательная заменяется на прямую, паралл. первой касательной Теорема о методе касательных. Если ф-ия f(a)*f(b)>0, причем вторая призводная сохраняет знак на отрезке [a,b], то исходя из любого начального приближения х0Є[a,b], удовл. условию f(х0) f”( х0)>0 то можно вычислить корень ур-я с любой степенью точности. Док-во: f(a)<0; f(b)>0; f”(x)>0; f’(x)>0, т.е. f(b) f”(b)>0 x0=b. Методом индукции докажем что, все xn>x*. Т.е. f(xn)>0, очевидно х0>x*. Путь хn>х*. Представим х*=хn+(х*-хn) по форм. Тейлора f(x*)=f(xn)+f’(xn) (х*-хn)+1/2 f”(xn) (х*-хn)2, тогда f(xn)-f’(xn) (х*-хn)<0 хn+1=xn(+)-f(xn)/f’(xn)>x*. Ч.т.д. |
||||||||||||||||||||||
|
Видоизмененный метод касательных.
X(n+1)=Xn-f(Xn)/
Комбинированный метод. f(x)=0 : (a,b) : f(a)*f(b)<0 имеем 4 случая: Расм. только 1-ой случай т.к. оставшиеся случаи либо сводяться к нему либо аналогичны. _
X* Є
(a,b) x0=a
x0=b
Если допустимая
погрешность задана u=E,
то как только
|
6. Метод итерации.
f(x)=0,
заменим это ур-е равносильным x=f(x)
и построим приближение x2=f(х1),…xn+1=f(x).
Если эта последовательность существует
и сходиться, т.е. сущ. Предел
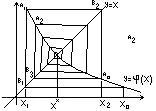
Если φ(х) возр. то получается лестницей, если убыв. то строится по спирали. |
||||||||||||||||||||||
|
Теорема о сходим. метода итерации. Пусть φ(х) опред. и диф. на [a,b] тогда, если сущ. дробь q такая |φ ‘ (x)|<=q<1 Тогда 1) процесс итерации А(n+1)=φ(Xn) сход. независ. от Х0.2) Предельн. знач-е явл. единств. корнем ур-ия LimXn=X*(n→бескон).Д-во: рассмотр. Хn=φ(X(n-1)); X(n+1)=φ(Xn); вычтем, по теорем. Лагранжа будем иметь a(n+1)-Xn=(Xn-X(n-1))*φ’(Xn( с чер.));|X(n+1)-Xn|<= q |Xn-X(n-1)|. Пусть n=1,2… Тогда.|X(n+1)-Xn|<=qn|Xn-X0|. Рассмотр. ряд Х0+(Х1-Х0)+(Х2-Х1)+… для этого ряда посл-ти приближен. явл. (n+1)-ми частными суммами Т.е. Xn=S(n+1) В силу неравенств все члены ряда < соотв. членов геом. прогрессии .У котор. знаменат. <1 поэт. ряд сход. абсолютно. LimSn+1=LimXn=X*(n-бескон.)-единств. решение.X(n+1)=φ(Xn), X*. Итер. процесс сход. тем быстрее, чем |φ ‘ (x)|<1. Оценка итер. процесса: |X*-Xn|<=q n /(1-q)*|X1-X0|. Рассм. как свести ур-ие к виду, удобн. для итерации. f(x)=0; x=x-λf(x)-ур-ие равносил. исходному. x-λf(x)=φ(x); [x=φ(x)];Пусть f ’(x) удовл. неравенству 0<m<f ‘(x)<M. Нужно подобр. такое λ чтоб |φ’(x)|=|1-λf ‘’(x)|<1;Т.к.рассматр. положит. знач-я, то модули можно снять. φ’(x)=1-λf ‘(x); 1-λM1<1-λm1<=q<1;Т.о. можно положить λ=1/M1 . Исходя из этого вычисл. q; q=1-m/M; Этот спос. удобен если извест. интервал, в котор. нах. точное знач-е корня. Если задан. Х0, то λ наход. из ур-ия 1-λf ‘ (X0)=0. |
7. Выбор коэффициента в методе итераций. Нужно учитывать что в у-ии х= φ(х), φ(х) должно удовлет усл φ(х)<1. Этого можно добиться таким способом Рассмотр ур-е F(x)=0 это ур-е равносильно х=х-ЛF(x)=> φ(х)=ч-ЛF(x), где парам Л выбирают таким образом что бы 0=<1-ЛF’(x)=<q<1 По условию задачи m1=<F’(x)=<M1(наиб и наим значение) на [a;b] => Л=1/M1 (Примечание (Л – лямбда))
Метод итераций
решения нелинейных систем второго
порядка
При локализации корня графич. способом, удобно эти значения применять за нулевое приблежение. Из 1-ого ур-я явно выразим х, а из 2-ого у.
Lim(n
|
||||||||||||||||||||||
|
8.Метод Ньютона. f(c чер.)(x)=0 f1(x1..xn)=0, fn(x1..xn)=0 предпол. что Xp(c чер.)=(X1p,…Xnp) найдено 1-ого из корней, тогда этот корень X=Xp(c чер.)+E(c чер.)p, где E(c чер.)p=(E1p…Enp). E-погрешн. f(x)= f(a)+ f ‘ (a)(x-a). Выпиш. это ур-ие в разв. виде fn(…Xnp+Enp)=fn(…Xnp)+f ‘ n(X1)*(…Xnp)*E1p+… +f ‘n(Xn)*(X1p…Xnp)*Enp. т.о f ‘(х)=W(X)=(матрица)( 1) f ‘1(Х1)… f ‘1Хn 2) f ‘nX1… f ‘nXn)- Якобиан Исход. сист. можно зап. в виде f(Xp)+W(Xp)Ep=0; Ep=-W(Xp)f(Xp). Итерац. процесс X(p+1)=Xp-W–1 (Xp)f(Xp). Теорема: пусть Х0-нач. приближ. причем вып. условия 1) W(X)-якобиан имеет обр. матр. Г0= W-1(x0), ||Г0||<=A 2)норма ||Г0f(x0)||<=B 3) сумма|δ2 fi/δXiδXj|<=C 4)множитель μ0=2nABC<1 . При выпол. этих услов. процесс сходится. X(p+1)=Xp-W-1(Xp)f(Xp). Модиф. метод Ньютона. На каждом шаге процесса Ньют. приход. обращать матрицу. Предпол. что W-1(Xp)(примерно =) W-1(x0). Тогда X(p+1)=Xp- W-1(x0)f(Xp)-эта ф-ла в точности совпад. с фор-лой метода прост. итерации.Теорема: при выполн. услов. 1) W(X)-якобиан имеет обр. матр. Г0= W-1(x0), ||Г0||<=A 2)норма ||Г0f(x0)||<=B 3) сумма|δ2 fi/δXiδXj|<=C 4)множитель μ0=2nABC<1 , модиф. метод Ньютона сход. к решению системы. |
9. Метод скорейшего спуска решения линейных систем
Есть система
Предположим, что
все fi
непр. дифф., рассм. Ф-цию U(x)
= (
U(
Пусть
выразим отсюда p и подставим значение U = 2WTf(x). В итоге получим: xp+1=xp-pWT(xp)f(xp), где p = 2p = (fp,WpWpTfp)/( WpWpTfp, WpWpTfp)
Для линейных
систем вида |
||||||||||||||||||||||
|
Метод скорейшего спуска решения систем.(grad) Grad-задаёт направление. Предположим что все fi непрерыв диф-мы Рассмотрим ф-ю u(x)=(_f(_x);_f(_x))= ф-я сама на себя скалярная = (i от 1 до n)(fi(_x))2. Очевидно что каждое решение исход сист обращ в 0 ф-ю u(x) и наоборот те числа обращают в 0 ф-ю u(x) явл решеним исх сист. Предположим что исх сист имеет лишь решения которые явл (.) мин ф-ии u таким образом задача сводится к нахождения (.) мин ф-ии u. Пусть _х – решение сист _х(0) – нулевое приблежение. В (.) _х(0) проведём поверхность уровня u(x)=u(xi0), если нач (.) близка к решению, то поверхность похожа на эллипсоид . Из(.) х(0) будем двигаться по нормали поверхности u(x)=u(x0) до тех пор пока нормаль не каснётся другой поверхности уровня u(x)=u(x(1)) Затем отправляемся из (.) х(1) по нормали поверхности уровня u=u(x(1)) до тех пор пока эта нормаль не каснётся поверхности уровня в (.) х(2) и т.д.
О (Примечание (Л – лямбда)) |
10. Формула ТРАПЕЦИИ. Разобьем отрезок [a; b]
н [x0,x1], [x0,x2], …, [x0,xn] шаг h = (b-a)/n yi=f(xi)
Ф-ла трапеции:
Нахождение остаточного члена формулы трапеций. Рассмотрим остаточный член для 1-го звена, а остальные просуммируем Предположим, что ф-ция f дважды дифференцируема. Получим ф-цию
R(h)
=
- (h/2)*y’(x0+h) = (1/2)*(y(x0+h) - y(x0)) - (h/2)*y’(x0+h) R”(h) = (1/2)*y’(x0 + h) - (1/2)*y’(x0 + h) - (h/2)*y”(x0 + h) = - (h/2)*y”(x0 + h) R(0)=R’(0)=R”(0)=0. Проинтегрируем по h и воспользуемся теоремой о среднем
Теперь просуммируем остаточные члены для одного звена и получим полный R(h) = - (h3/12)*y”(ci), ci(xi-1, xi) Далее, (.) c[a, b], такая что (y”(ci))/n = y”(c) => R(h) = - (h3/12)*n*y”(c) => R(h) = - (b-a)*h2*y”(c)/12, c[a, b] На практике: Ih = h + Mh2, I2h = 2h + 4Mh2 => R = (h - 2h)/3 |
||||||||||||||||||||||
|
11.Формула СИМПСОНА (парабола).
∫f(x)dx
(рис.). Число разбиен. должно делиться на 4, чтобы можно было вычислить суммы с шагом 2h. Пары интервалов, следующие друг за другом, начиная с первой, будем “накрывать” параболой, проход. через 3 (.)-ки y=A0+A1x+A2x2; (x0,y0), (x1,y1), (x2,y2). Предпол что x0 = 0 => x1 = h, x2 = 2h. Для нахожд. A0,A1,A2 подстав. эти (.)-ки в ур-ие параб. => y0 = A0; y1 = A0+A1h+A2h2; y2=A0+2A1h+4A2h2; Получим, A0 = y0; A1 = (-3y0 + 4y1 - y2)/2h; A2 = (y0 - 2y1 + y2)/2h2
Площадь одного
эл-та (зависит от h
и значений ф-ции в выбранных точках)
=
Подставл знач-я А0, А1, А2 получ. In=(h/3)*(yn-2 + 4yn-1 + yn);
In
=
|
Оценка погрешности в методе Симпсона. Предположим, что ф-я y непрерывна и трижды дифференцируема. Запишем ошибку для первого интервала в виде:
Продифференцируем эту ф-ю 3 раза. R’(h) = y(x1+h) – y(x1-h) – (1/3)[y(x1-h) + y(x1+h) + 4y(x1)] – (h/3)*[-y’(x1 – h) + +y’(x1+h)] R”(h) = - (1/3)y’(x1-h) + (1/3)y’(x1+h) – (h/3)[y”(x1-h) + y”(x1+h)] R”’(h) = -(h/3)[y”’(x1-h) - y”’(x1+h)] = -(2h2/3)*yIV(c4), c4(x1-h, x1+h) Теперь будем интегрировать:
R”(h)
=
R’(h) =
R(h)
=
На практике: Rh = Mh4, R2h = 16Mh4; R = (h - 2h)/15 |
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
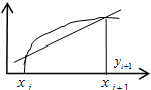
12. Метод Эйлера решения дифференциальных уравнений
y’=f(x,y); y(x0) = y0 - задача Коши. Разобьем ось х на промежут. xi = x0+i*h (рис.) В (.)M0-пров. касател. до пересеч. с прямой х = х1, получим (.)M1. y1 = х1 M1 Через (.) (x1, f(x1, y1)) пров касат до пересечения с прямой x = x2, получим M2 и тд Получ. Ломаную M0M1M2… считаем решением. Аналитически: f(xi,yi) = y’ (yi+1 - yi)/h => yi+1 = yi + h*f(xi,yi)-ф-ла облад. малой точностью.(порядка h2); y(xi+h)=y(xi)+y’(xi)h остал. члены разлож. в ряд Тэйлора (y(x)=y(x0)+y’(x0)(x-x0)+y”(x0)(x-x0)2/2!-поэт. точность порядка h2. Модифицированный метод Эйлера. В отличии от метода Эйлера, когда для вычисления следующей точки (Xi+1, Yi+1) требуется информация только Y предыдущей точки. Мод. метод предполагает знание о нек-ой промежуточной точки xi+1/2=xi+h/2 и xi+1/2=xi+(h/2)*fi. Метод заключается: 1) через точку (xi,yi) проводится кас-ая с tg наклона tgα=f(xi,yi) до х с прямой x=xi+1/2. В полученной точке х по методу Эйлера выч-ся знач-я ф-ии y=yi+1/2 и выч-ся знач-е производной fi+1/2=f(xi+1/2, y=yi+1/2). Знач-е этой производной определяет tg угла наклона 2-ой производной, кот. проводится из полученной точки. 2) Затем возвр-ся в исходную точку и через неё проводим прямую, парал 2-й кас-ой. |
Усовершенствованный метод Эйлера.
Метод Рунге-Кутта.
Обычно говорят,
что метод Р-К явл. Методом 4 и 5 порядка
точности, т.е. (h4,h5).
Точно вычислить погрешность этого
метода затруднительно, т.к. исходя из
текущего значения y(xi)
вычисляют величину y(xi+2h)
2-мя способами. 1 раз с шагом h,
другой с шагом 2h.
Если расхождение полученных значений
не превышает допустимой погрешности,
то шаг выбран правильно и полученное
значение можно принять за верное, в
противном случае шаг уменьшают в 2
раза. Мы решаем ур-е
Выбирается шаг
h,
наносится сетка xi+1=x0+hi.
Рассматривают
числа
k1(i)=h*f(xi,yi);
k2(i)=h*f(xi
|
||||||||||||||||||||||
|
13 .Метод прогонки Будем рассматривать д.у 2 порядка: y” +p(x)y’+q(x)y =f(x) при заданных условиях α0y(a)+ α1y’(a)=A β0y(b)+ β1y’(b)=B │α0│+│α1│≠0 │ β0│+│ β1│≠0 Исходная система может быть представлена в виде разностной схемы (yi+1–2yi+yi-1)/h2+pi(yi+1-yi-1)/2h +qiyi=fi (1), где pi, qi, fi –значения коэффициентов в точках xi. α0y0+ (α1(y1-y0))/h=A β0yn+ (β1(yn-1-yn))/-h=B Будем использовать метод прогонки Из ур (1) можно получить yi+1+miyi+niyi-1=f^ih2 (4) где коэффициенты имеют вид: mi=(2-qih2)/(1+pih/2) ni= (1-pih/2)/(1+pih/2) f^i=fi/(1+pih/2) Из уравнения (4) выразим yi yi=f^ih2/mi – (1/mi)(yi+1)-(ni/mi)(yi-1) (5) Предположим, что с помощью системы (2), (3), (4) из ур-ния (5) исключено yi-1,тогда yi= ci(di-yi+1) (6) Из ур (6) можно записать yi-1= ci-1(di-1-yi) Подставляя это уравнение в ур-ние (4) получим yi+1+miyi+nici-1di-1-yi=f^ih2 Отсюда выразим yi yi=( f^ih2- nici-1di-1-yi+1)/(mi-nici-1) Исходя из сравнения полученных формул получим ci=1/mi-nici-1 di=f^ih2-nici-1di-1 c0= α1/ (α0h - α1) d0=Ah/ α1 На основании этих формул последовательно определяются сi и di при i=1 до n-1 включительно Обратный ход начинается с вычисления yn Вычислив yn по ф-ле (6) определяются все остальные значения y |
14.Уравнение Лапласа в конечных разностях
Б
|
||||||||||||||||||||||
|
Метод сеток. Построение шаблонов Пусть в плоскости XOY имеется область G с границей Г, построим на плоскости два семейства параллельных прямых x= x0+ih y=y0+kh
В
|
16. Интерполирование функций. Постановка задачи.
П
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
Метод наименьших квадратов. (матем. обработка данных).Пусть в рез-те исслед. некоторой величины Х знач-я Х1,Х2…Хn поставлены в соответствие др. знач-я …Xn→y1,y2…yn; Треб. подобрать вид аналитич. записи y=y(x) связыв. перемен. х и у; В задаче треб. найти некую прямую y=bx; Задача закл. в определен. пост. b; В методе наим. квадр. параметр b опред. из условий min суммы квадратов отклонений эксперим. данных yi от расчетных величин yi*; F=∑(от 1 до бесконеч.)(yi-bxi)2→min; δF/δb =2∑((yi-bxi)*(-xi))=0; b=(∑xiyi)/(∑xi2); В нек. случаях иском. прям. имеет вид y=a+bx; F=∑(yi-a-bxi)2→min; δF/δb=2∑[(yi-a-bxi)(-xi)]; ∑(yixi-axi-bxi2)=0; ∑yixi=∑(axi)+∑bxi2; ∑xiyi=a∑xi+b∑xi2; a= (∑yi-b∑xi)/n; n∑xiyi=∑xiyi-b(∑xi)2+bn∑xi2; b=(n∑xiyi-∑xi∑yi)/(n∑xi2-(∑xi)2).
|
17. Формула Лагранжа.
Будем считать
данную ф-ию f(x)
и полином Qm(x)=a0+a1x+a2x2…+amxm
близкими, если они совпадают на заданной
системе точек x0,x1,x2…xn.
Задача состоит в том, чтобы построить
многочлен возможно низшей степени m,
принимающий в данных точках известные
значения. По основной теореме алгебры
можно предположить, что m=n.
Исходя из условия задачи, можно записать
систему линейных уравнений.
|
||||||||||||||||||||||
|
18.Формула Ньютона для разностных узлов. ∆y0 = y1-y0 ∆y1= y2-y1 ∆y2= y3-y2 ∆yn-1 = yn - yn-1 ∆y0 = y1-y0 ∆2y0 = ∆y1- ∆y0 = y2 – y1 – y1 + y0 = y2 – 2y1 + y0 ∆3y0= ∆2y1- ∆2y0 = y3 – 3y2 +3y1 – y0 ∆ky0 = yk – kyk-1 + ((k(k-1))/2!)yk-2 + ((k(k-1)(k-2))/3!)yk-3 + ...+ (-1)Ky1 Запишем эту формулу для значения разности в узле xi: ∆kyi = yk+i – yk+i-1 + ((k(k-1))/2!)yk+i-2 yk=y0 +k∆y0 +((k(k-1)/2!)∆2y0 + … ∆ky0 Построим интерполяционный многочлен Ньютона: N(x)= a0 +a1(x-x0) +a2(x-x0)(x-x1) +a3(x-x0)(x-x1)(x-x2) + … an(x-x0)(x-x1)…(x-xn-1) Этот многочлен должен проходить через заданные узлы, поэтому: N(x0)= a0=y0 N(x1)= a0 +a1(x-x0) = a0 + a1h=y1 N(x2)= a0 +2a1h+ 2a2h2 = y2 Отсюда найдём коэффициенты: a0=y0 a1= (y1-y0)/h=∆y1/h a2=∆2y0/2h2 Следовательно, любой коэффициент имеет вид: ak = ∆ky0/k!hK и полином Ньютона будет иметь вид: N(x)=y0+ (∆y0(x-x0))/h + (∆2y0(x-x0)(x-x1))/2!h2 + … + (∆ny0(x-x0)(x-x1)…(x – xn-1))/n!hn Запишем его иначе: пусть (x-x0)/h =q тогда N(x) =(y0 +q∆y0∆2y0q(q-1))/2! + … + ∆ny0(1/n!)q(q-1)(q-2)…(q-n+1) Многочленами Ньютона пользуются в случае равноотстоящих узлов. |
Приближенное дифференцирование. Постановка краевых задач
Пусть имеем
функцию y(x)
заданную в равноотстоящих точках.
Запишем многочлен Ньютона для этой
функции y(x)=
y0+q∆y0+(q(q-1)
∆2y0)/2
+ (q(q-1)(q-2)∆3y0)/3!
+ (q(q-1)(q-2)(q-3)∆4y0)/4!
Для нахождения производной функции
будем искать производную этого
многочлена h=xi+1-xi;
q=(x-x0)/h
y(x)=
y0+q∆y0+
((q2-q)∆2y0)/2+((q3-3q2+2q)∆3y0)/3!
+ ((q4-6q3+4q2-6)
∆4y0)/4!+…
|
||||||||||||||||||||||
|
19. Абсолютная и относительная погрешность.
Абсолютной
погрешностью приближенного значения
а* называется величина
|
|

 )a>0
)a>0
 (n+1)=Xn-(f(Xn)/
f
‘ (Xn))>X*.
(n+1)=Xn-(f(Xn)/
f
‘ (Xn))>X*.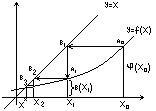
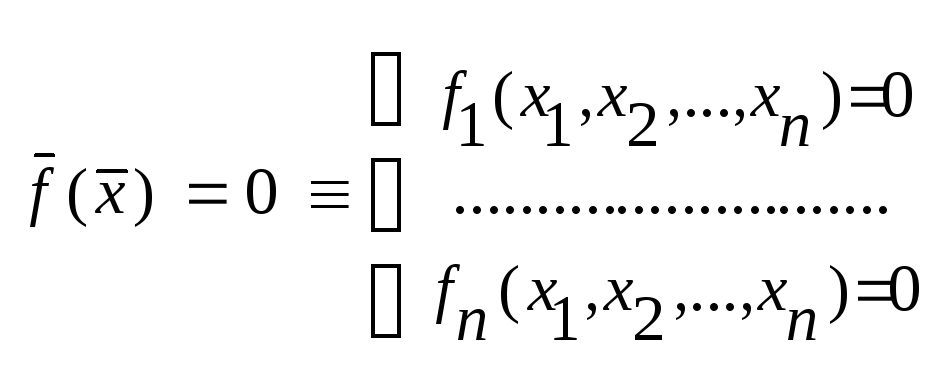

 а
n
равных отрезков
а
n
равных отрезков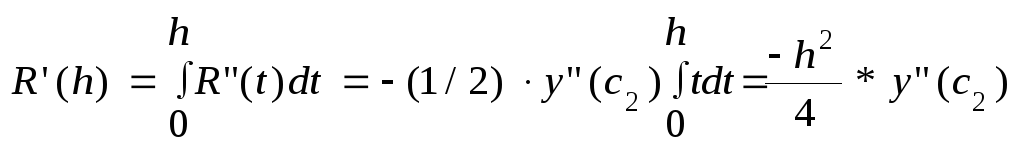 ,
c2(x0,
x0+h)
,
c2(x0,
x0+h)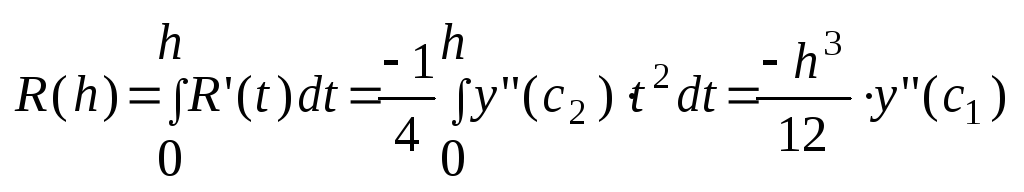 ,
c1(x0,
x0+h)
,
c1(x0,
x0+h)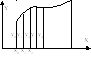
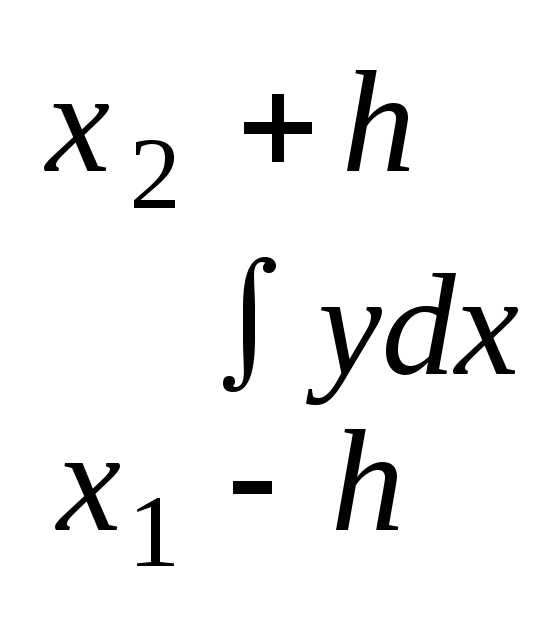 -
(h/3)*[y(x1-h)
+ 4y(x1)
+ y(x1+h)]
-
(h/3)*[y(x1-h)
+ 4y(x1)
+ y(x1+h)]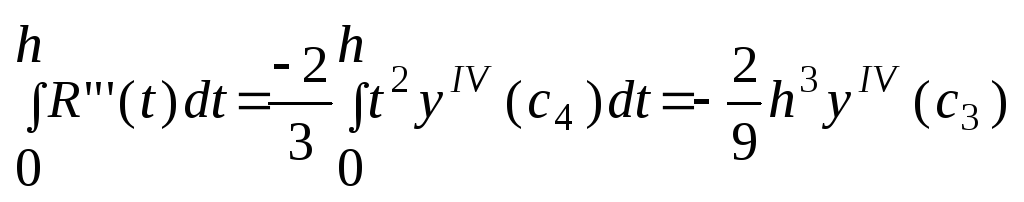 ,
c3(x1-h,
x1+h)
,
c3(x1-h,
x1+h)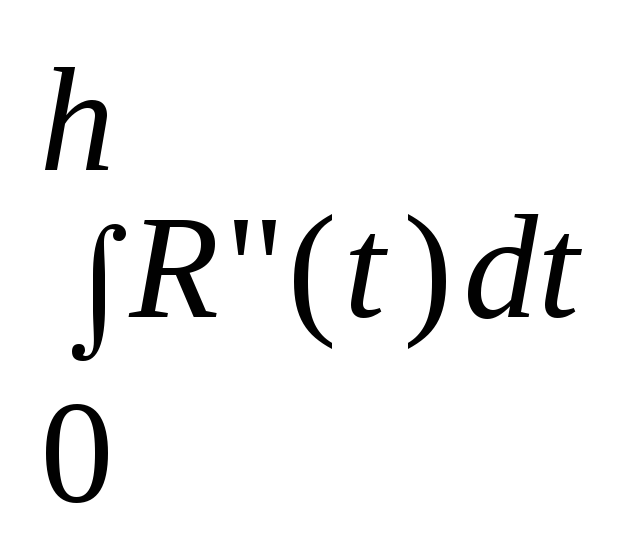 =
-(1/18)*h4*y4(c2),
c2(x1-h,
x1+h)
=
-(1/18)*h4*y4(c2),
c2(x1-h,
x1+h)




 ерез
точку (xi,yi)
проводится касс-ая до х с прямой
xi+1/2=xi+h.
Угл. коэф-т этой кривой tgα1=f(xi,yi).
2) В полученной точке по методу Эйлера
выч-ся знач-е ф-ии yi+1=yi+h*(
f(xi,yi))
и выч-ся новая производная tg
α2=
f(xi,yi+1).
3) Далее происходит возврат в точку
(xi,yi)
и через нее проводится новая касательная,
где tg
угла наклона есть среднее арифметическое
2-ух предыдущих tg-енсов,
т.е. tgα
= (tgα1+
tgα2)/2
= (f(xi,yi)+F(xi+1,yi+1))/2.
Новое значение yi+1
= yi+h*((f(xi,yi)+F(xi+1,yi+1))/2).
ерез
точку (xi,yi)
проводится касс-ая до х с прямой
xi+1/2=xi+h.
Угл. коэф-т этой кривой tgα1=f(xi,yi).
2) В полученной точке по методу Эйлера
выч-ся знач-е ф-ии yi+1=yi+h*(
f(xi,yi))
и выч-ся новая производная tg
α2=
f(xi,yi+1).
3) Далее происходит возврат в точку
(xi,yi)
и через нее проводится новая касательная,
где tg
угла наклона есть среднее арифметическое
2-ух предыдущих tg-енсов,
т.е. tgα
= (tgα1+
tgα2)/2
= (f(xi,yi)+F(xi+1,yi+1))/2.
Новое значение yi+1
= yi+h*((f(xi,yi)+F(xi+1,yi+1))/2).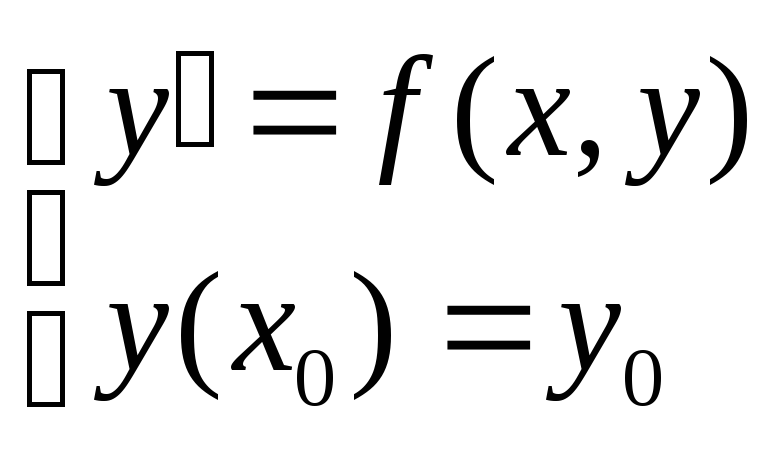
 удем
решать δ2u/δx2+
δ2u/δy2=0
Будем
решать задачу Дирихле, т.е найдём
решение уравнения Лапласа в заданной
области, ограниченной контуром гамма
причём u(p)=φ(p)
PГ
для всех точек p
принадлежащих границе.Т.е на границе
области задана непрерывная функция.
Перейдём от дифура к его разностному
аналогу δ2u/δx2=
=(u(x+h,y)-2u(x,y)+u(x-h,y))/h2
δ2u/δy2=(u(x,y+h)-2u(x,y)+u(x,y-h))/h2
Подставим
u(x,y)=1/4(u(x+h,y)+u(x-h,y)+
u(x,y+h)
+u(x,y-h))
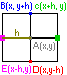
Это уравнение соответствует первой
разностной схеме. 1 осн схема изображена
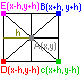
на левом рисунке. 2 осн сх:
u(x,y)=1/4(u(x+h,y+h)+u(x+h,y-h)+
u(x-h,y-h)
+u(x-h,y+h))
И 1 и 2 схема являются точными до порядка
h2
удем
решать δ2u/δx2+
δ2u/δy2=0
Будем
решать задачу Дирихле, т.е найдём
решение уравнения Лапласа в заданной
области, ограниченной контуром гамма
причём u(p)=φ(p)
PГ
для всех точек p
принадлежащих границе.Т.е на границе
области задана непрерывная функция.
Перейдём от дифура к его разностному
аналогу δ2u/δx2=
=(u(x+h,y)-2u(x,y)+u(x-h,y))/h2
δ2u/δy2=(u(x,y+h)-2u(x,y)+u(x,y-h))/h2
Подставим
u(x,y)=1/4(u(x+h,y)+u(x-h,y)+
u(x,y+h)
+u(x,y-h))
Это уравнение соответствует первой
разностной схеме. 1 осн схема изображена
на левом рисунке. 2 осн сх:
u(x,y)=1/4(u(x+h,y+h)+u(x+h,y-h)+
u(x-h,y-h)
+u(x-h,y+h))
И 1 и 2 схема являются точными до порядка
h2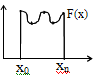 усть
на [a,b]
заданы (n+1)
точек x0,x1,…,xn
(эти точки наз-ся узлами интерполяции).
Известны значения нек-ой ф-ии в этих
точках: f(x0)=y0,
f(x1)=y1,
f(xn)=yn.
По этим точкам требуется построить
ф-ю F(x),
принадлежащую известному классу,
принимающую в узлах интерполяции
известные знач-я. В такой интерполяции
ф-ия F(x)
либо не однозначна, либо не сущ-ет
вовсе. Если же ф-ия F(x)=Pn(x)
имеет вид полинома степени не выше
степени n,
то такая задача имеет единственное
решение. Полученную интерполяционную
ф-ию F(x)
используют для нахождения значений
ф-ии в точках, отличных от узлов
интеропляции. Если эти точки принадлежат
промежутку [a,b],
то такая задача наз-ся интерполированием
в узком смысле. Если же точки выходят
за границы [a,b],
то такая задача наз-ся экстраполированием.
усть
на [a,b]
заданы (n+1)
точек x0,x1,…,xn
(эти точки наз-ся узлами интерполяции).
Известны значения нек-ой ф-ии в этих
точках: f(x0)=y0,
f(x1)=y1,
f(xn)=yn.
По этим точкам требуется построить
ф-ю F(x),
принадлежащую известному классу,
принимающую в узлах интерполяции
известные знач-я. В такой интерполяции
ф-ия F(x)
либо не однозначна, либо не сущ-ет
вовсе. Если же ф-ия F(x)=Pn(x)
имеет вид полинома степени не выше
степени n,
то такая задача имеет единственное
решение. Полученную интерполяционную
ф-ию F(x)
используют для нахождения значений
ф-ии в точках, отличных от узлов
интеропляции. Если эти точки принадлежат
промежутку [a,b],
то такая задача наз-ся интерполированием
в узком смысле. Если же точки выходят
за границы [a,b],
то такая задача наз-ся экстраполированием.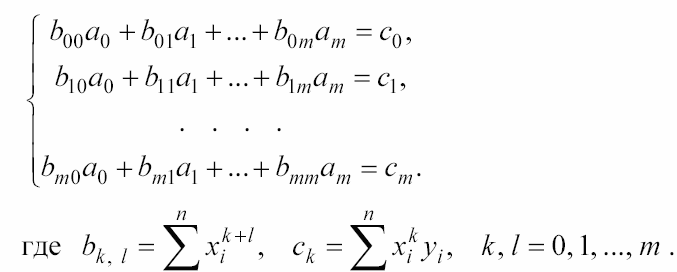
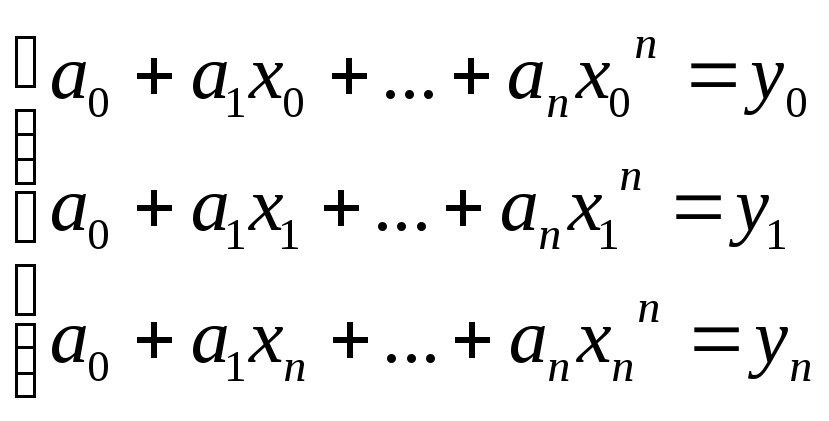 .
Эта система линейная, её можно решать
по формуле Крамера (определитель
Вандермода): Δ=
.
Эта система линейная, её можно решать
по формуле Крамера (определитель
Вандермода): Δ=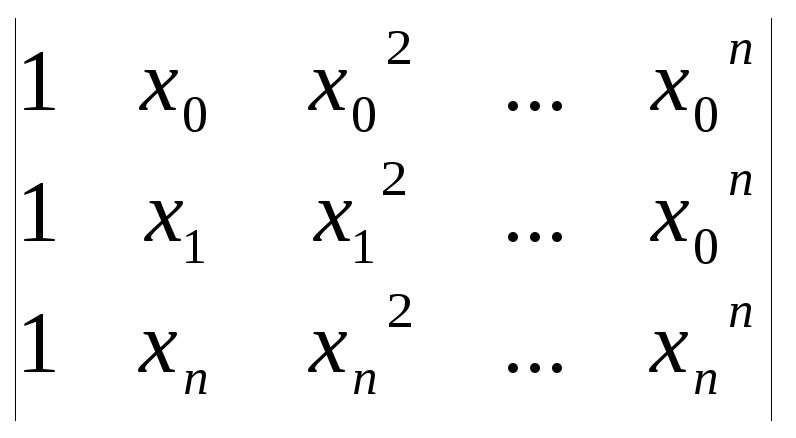 =П(xq-xp)
– произведение, где
=П(xq-xp)
– произведение, где