2. Разработка основных технических требований на устройство определения динамических характеристик

Наряду с перечисленными в разделе 1 общими требованиями к устройству необходимо дополнительно рассмотреть группу частных технических вопросов. Это позволит с учетом рекомендаций по обеим группам сформулировать общие технические требования на устройство. В качестве основных вопросов такого рода необходимо назвать следующие:

-определение метода, частотного диапазона измерения и диапазона автоматической перестройки частоты функционального генератора;

-определение требуемого динамического диапазона измерения входных и выходных сигналов:

-предварительное определение принципов идентификации динамических характеристик;

-определение номинальных значений сигналов измерения и возмущения для измерительной части устройства.

2.1 Определение метода и частотного диапазона измерений

На основании анализа, проведенного в предыдущей главе, минимальным значением постоянной времени элемент а электромеханической системы регулирования можно принять значение Т=10 мс. Отдельные электромеханические преобразователи (маломощные электромагниты устройств «сопло-заслонка», высокочастотные электродинамические преобразователи) также могут иметь постоянные времени порядка единиц миллисекунд

Большинство элементов электромеханических систем имеет передаточную функцию типа апериодического или колебательного звена с частотой, определяемой как частота среза (для апериодического звена) или резонансной частотой (для колебательного звена).

Диапазон измерений по данным литературы [1,52] должен превышать частоту среза не менее чем на декаду. Для апериодического звена частота среза fs=l/2/71/Т, где Т - постоянная времени звена. Значение частоты среза для Т 1 мс - fs--1 /2/зт/10'3 = 150 Гц.

Для колебательного звена можно принять частоту среза равной f = 0.7*fo, где f0 - первая собственная частота колебательного звена.

Таким образом, верхняя граница измерения устройства для определения динамических характеристик исполнительных элементов электромеханических систем может быть принята равной 1500.. .2000 Гц.

Максимальные значения постоянных времени элементов электромеханических систем достигают 10...50с, то есть эти элементы имеют частоту среза Ј,=1/2/я/50 = 3*10'’ Гц. Исходя из этого, а также и рекомендаций [1,52], нижняя граница частотого диапазона о устройства должна иметь значение не более 10" Гц.

Однако, в соответствии с [2,40] непосредственные измерения частотных

характеристик целесообразно проводить на частотах не ниже 0,5 1 Гц. На более низких

частотах рекомендуется использовать вычисления частотной характеристики по экспериментально определенной переходной характеристике элемента [8,41]. Это позволяет сократить время измерения. Частота условного раздела, при которой время прямого измерения частотных характеристик приблизительно равно времени вычисления частотных характеристик по переходной характеристике, находится в пределах 1...5 Гц [10]. Поэтому измерение динамических характеристик элементов, характерные частоты которых находятся вблизи указанного выше диапазона, можно проводить любым из этих методов.

Таким образом, представляется очевидно необходимым организовать в устройстве определения частотных характеристик две возможности подачи возмущающего сигнала:

• синусоидального сигнала с частотой, изменяемой в диапазоне 0,2...2000 Гц для непосредственного определения частотных характеристик; ступенчатого сигнала для определения переходных характеристик.

Измерительная часть устройства также должна реализовывать два режима определения частотных характеристик:

• непосредственное измерения модуля и фазы передаточной функции при возбуждении элемента синусоидальным сигналом;

вычисление модуля и фазы передаточной функции по измеренной переходной характеристике объекта.

Отдельного рассмотрения требует вопрос о применении спектрального частотного метода для определения передаточных функций элементов электромеханических систем путем возбуждения элемента сигналом белого шума и определения спектра выходного сигнала с последующим определением частотных характеристик. На этом принципе работает большинство промышленных анализаторов (например, типа 2032 и 2034 фирмы Bruel&Kjaer и аналогичные им анализаторы других фирм). Применение такого метода исторически вытекало из необходимости решения задач акустических измерений и было механически перенесено на измерения характеристик электрических и электромеханических устройств.

В литературе, посвященной измерению частотных характеристик [2,10,40,48], высказывается мнение, что этот метод создает затруднения при определении дифференциальных коэффициентов передачи элементов с нелинейными проходными характеристиками. Однако анализа этих затруднений и точности измерений в литературе не приводится.

Анализ характеристик электромеханических элементов, проведенный в разделе 1, показывает, что многие электромеханические элементов обладают нелинейными характеристиками. Поэтому вопрос о погрешностях определения дифференциальных коэффициентов передачи таких элементов является весьма существенным.

Преобразование одномерного шумового сигнала у= x(t) при прохождении через нелинейный элемент в общем случае по [3] определяется двумя выражениями:

где g(x) - нелинейная функция;

- дифференциальная плотность распределения вероятности входного сигнала;

- математическое ожидание выходного сигнала;

а _у - среднеквадратичное отклонение.

Учитывая, что для “белого” шума:

можно записать общие выражения для определения математического ожидания и дисперсии выходного шумового сигнала:

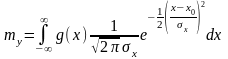
(2.1)

Эти выражения для достаточно произвольных значений g(x) и не приводятся к

элементарным функциям. Очевидно, поэтому в литературе приводятся результаты аналитических вычислений такого рода только для функций g(x), представленных в виде кусочно-линейных аппроксимаций [3,34], либо для функции р_х, представленной в виде равномерного распределения.

Большинство нелинейных электромеханических элементов имеют проходную характеристику, близкую к квадратичной или кубической (рис.2.1).

Рис.2.1. Проходная характеристика нелинейного элемента

Для этого случая выражения (2.1) приобретают вид:

_{,n=2,3 (2.2)}

В случае возбуждения такого нелинейного элемента синусоидальным сигналом выражение для выходного сигнала элемента с квадратичной и кубической проходной характеристикой имеют следующий вид:

_(n=2)

Где

В этих выражениях можно выделить следующие составляющие: величина /га_у

соответствует постоянной составляющей выходного сигнала, включающей и продетектированное значение входного сигнала; величина представляет собой

линеаризованную составляющую выходного сигнала с частотой возбуждения, характеризующую дифференциальный коэффициент передачи элемента в точке х₀, а

величина у₂ характеризует погрешность определения дифференциального коэффициента передачи. Строго говоря, в погрешность дифференциального коэффициента передачи должнавключаться также продетектированная постоянная составляющая входного сигнала, однако этого можно избежать программными или схемотехническими методами.

Для численного определения значений т_у и о_у был разработан алгоритм и

программа, приведенная в Приложении 4 работы

На рис.2.2 приведены зависимости погрешности определения динамического коэффициента передачи элементов с квадратичной и кубической проходными

характеристиками в зависимости от отношения и для случаев возбуждения

синусоидальным сигналом и сигналом белого шума

Рис.2.2. Погрешность определения коэффициента передачи

Эти характеристики позволяют сделать следующие выводы

• погрешность определения дифференциального коэффициента передачи как для шумового, так и для синусоидального сигнала возбуждения практически монотонно

возрастает с увеличением отношения ;

-погрешности измерения дифференциального коэффициента передачи для элемента с квадратичной проходной характеристикой практически одинаковы при равных значениях

-погрешность измерения дифференциального коэффициента передачи для элемента с кубической проходной характеристикой оказывается существенно выше при возбуждении шумовым сигналом, чем при возбуждении синусоидальным сигналом при равных .

Можно считать, что для характеристик со степенями не выше квадратичной, определение коэффициента передачи путем возбуждения синусоидальным и шумовым сигналом является равноценным с точки зрения погрешности измерения. Это, на первый взгляд, противоречит устойчивому мнению, что погрешности при определении характеристик нелинейных элементов при возбуждении шумовым сигналом оказываются большими.

Это мнение, очевидно, объясняется следующим обстоятельством. При выводе выражений (2), среднеквадратичное значение шумового сигнала в заданной полосе измерения две декады принималось равным среднеквадратичному значению детерминированного синусоидального сигнала. Такое допущение предполагает, фактически, равную мощность детерминированного синусоидального сигнала и шумового сигнала в полосе измерений (две декады). Мощность шумового сигнала по [40] определяется, как

со

где

Для сигнала белого шума это выражение можно записать, как

Цифровой анализатор, построенный на базе преобразований Фурье, измеряет амплитудное или среднеквадратичное значение шумового сигнала в элементарной полосе анализа. Общая мощность шумового процесса в полосе анализа определяется по [40] выражением:

где G=const - спектральная плотность мощности D_w - общий диапазон измерений.

Таким образом, величина среднеквадратичного значения белого шума в элементарной полосе анализа

Так как где n-число элементарных частотных полос анализа

таким образом,

Например, для числа элементарных полос N=100 в общей полосе анализа, среднеквадратичное значение сигнала, приходящееся на элементарную полосу, будет в десять раз меньше. Это не имеет значения при идеальных условиях измерения, однако, при ограниченной чувствительности анализатора, потребуется определенное увеличение входного шумового сигнала для обеспечения его нормальной работы. Однако при этом возрастут и погрешности измерения сигнала, определяемые выражением (2.3).

Очевидно, что указанное явление и объясняет существующее мнение о большей погрешности измерения проходных нелинейных характеристик элементов при шумовом возмущающем сигнале. Для определения динамических характеристик элементов, работающих в системах с высокими уровнями шумов, статистический метод возможно даст более достоверные результаты. Поэтому в измерительной части проектируемого устройства предусмотрена возможность использования данного метода (при наличии генератора «белого шума»).

Следующим важным вопросом является определение требуемого диапазона автоматического сканирования частоты в процессе измерения частотной характеристики. В разных источниках приводятся различные требования по ширине этого диапазона, который колеблется от одной декады [34] до трех декад [10]. Измерительные приборы фирмы В&К работают в полосе частот шириной в три декады, однако эти приборы предназначались первоначально и, в большинстве случаев, используются для измерения частотных характеристик звуковоспроизводящей аппаратуры в стандартной для этой аппаратуры полосе частот [5]. В примерах [8] основные особенности передаточных функций анализируются в основном в полосе частот - две декады.

Стандартные функциональные генераторы с внешним управлением частотой имеют диапазон сканирования частоты 1...100, то есть две декады. Такой же диапазон имеют приборы, построенные на специализированных микросхемах (например, МАХ 038 фирмы MAXIM). По данным фирм, расширение диапазона сканирования частоты более двух декад приводит к возможности появления паразитной частотной модуляции выходного сигнала из- за наличия помех в цепях управления.

Исходя из сказанного, можно считать приемлемой ширину диапазона автоматического сканирования частоты функционального генератора устройства в две декады при общей ширине частотного диапазона функционального генератора и измерителя в пределах 0,2...2000 Гц, то есть четыре декады.